Connecting Isles

Logic Level 3

Find the total number of distinct ways to join the six islands below by bridges such that

each island can be reached from any other island via the bridges,
1 of the islands has 1 bridge leading from it,
2 of the islands each have 2 bridges leading from them, and
3 of the islands each have 3 bridges leading from them.

Details and Assumptions:

Neither of the 2 islands on the far left can be joined directly to either of the 2 islands on the far right.
There can be more than 1 bridge between 2 islands.
Mirror images and 180-degree rotations are not counted as distinct.
No two bridges can intersect with each other.

Adapted from a Puzzle book.

The answer is 71.

2 solutions

Thanos Petropoulos
Feb 4, 2020

I agree with Thanos Petropoulos that the answer should be 71. I found this answer using a Python script. What follows is a list of the 71 bridge networks I found, a description of how I wrote the script to find them, and the script itself.

Label the islands A, B, C, D, E, and F clockwise from the top left. Number the eleven possible bridges according to the following list.

The 71 different bridge networks are listed below.

(1, 1, 2, 5, 7, 9, 11)
(1, 1, 2, 6, 7, 11, 11)
(1, 1, 2, 6, 10, 11, 11)
(1, 1, 2, 7, 7, 9, 11)
(1, 1, 2, 7, 9, 10, 11)
(1, 1, 2, 7, 9, 11, 11)
(1, 1, 3, 5, 7, 10, 11)
(1, 1, 3, 5, 7, 11, 11)
(1, 1, 5, 6, 7, 11, 11)
(1, 1, 5, 7, 7, 9, 11)
(1, 1, 5, 7, 9, 10, 11)
(1, 4, 4, 6, 7, 10, 11)
(1, 4, 4, 6, 7, 11, 11)
(1, 4, 4, 6, 10, 11, 11)
(1, 4, 4, 7, 7, 9, 10)
(1, 4, 4, 7, 7, 9, 11)
(1, 4, 4, 7, 9, 10, 11)
(1, 4, 5, 6, 7, 9, 11)
(1, 4, 5, 6, 7, 11, 11)
(1, 4, 5, 6, 8, 11, 11)
(1, 4, 5, 6, 9, 11, 11)
(1, 4, 5, 6, 10, 11, 11)
(1, 4, 5, 7, 7, 9, 9)
(1, 4, 5, 7, 7, 9, 11)
(1, 4, 5, 7, 8, 9, 11)
(1, 4, 5, 7, 9, 9, 11)
(1, 4, 5, 7, 9, 10, 11)
(1, 4, 5, 7, 9, 11, 11)
(1, 4, 6, 6, 7, 11, 11)
(1, 4, 6, 6, 10, 11, 11)
(1, 4, 6, 7, 7, 9, 11)
(1, 4, 6, 7, 9, 10, 11)
(1, 4, 6, 7, 9, 11, 11)
(1, 4, 6, 7, 10, 11, 11)
(1, 4, 7, 7, 9, 9, 10)
(1, 4, 7, 7, 9, 9, 11)
(1, 4, 7, 7, 9, 10, 11)
(1, 5, 5, 6, 8, 9, 11)
(1, 5, 5, 6, 8, 11, 11)
(1, 5, 5, 6, 9, 11, 11)
(1, 5, 5, 7, 8, 9, 9)
(1, 5, 5, 7, 8, 9, 11)
(1, 5, 5, 7, 9, 9, 11)
(1, 5, 6, 6, 8, 11, 11)
(1, 5, 6, 6, 9, 11, 11)
(1, 5, 6, 7, 8, 9, 11)
(1, 5, 6, 7, 9, 9, 11)
(1, 5, 6, 7, 9, 11, 11)
(1, 5, 6, 8, 9, 11, 11)
(1, 5, 7, 7, 8, 9, 9)
(1, 5, 7, 7, 9, 9, 11)
(1, 5, 7, 8, 9, 9, 11)
(3, 4, 4, 5, 7, 10, 11)
(3, 4, 4, 5, 7, 11, 11)
(3, 4, 4, 5, 10, 11, 11)
(3, 4, 5, 5, 7, 9, 11)
(3, 4, 5, 5, 7, 11, 11)
(3, 4, 5, 5, 8, 11, 11)
(3, 4, 5, 5, 9, 11, 11)
(3, 4, 5, 5, 10, 11, 11)
(3, 4, 5, 6, 7, 11, 11)
(3, 4, 5, 6, 10, 11, 11)
(3, 4, 5, 7, 7, 9, 11)
(3, 4, 5, 7, 9, 10, 11)
(3, 4, 5, 7, 9, 11, 11)
(3, 4, 5, 7, 10, 11, 11)
(3, 5, 5, 6, 8, 11, 11)
(3, 5, 5, 6, 9, 11, 11)
(3, 5, 5, 7, 8, 9, 11)
(3, 5, 5, 7, 9, 9, 11)
(3, 5, 5, 7, 9, 11, 11)

The script I used treats each bridge network as a graph with six vertices A through F and with seven of the bridges as edges. To preserve connectivity, an edge cannot appear three or more times. Therefore, the script considers edge sets with seven edges chosen from the multiset { 1, 1, 2, 2, . . . , 11, 11 }.

Calculating degrees. Given an edge set, the degree of a vertex in the corresponding graph can be found by counting the number of times an incident edge appears in the edge set. The incidences are given in the following table.

vertex	incident edges
A	1, 2, 3
B	3, 4, 6 8, 9
C	9, 10, 11
D	7, 8, 11
E	2, 5, 6, 7, 10
F	1, 4, 5

Identifying edge crossings. The only pairs of edges that cross are 2, 4 and 8, 10. As long as an edge set does not include one of these pairs, it has no edge crossings.

Testing connectivity. Any graph with the correct degree numbers will necessarily have no isolated vertices. Consider the graph with all eleven possible edges. There are nine sets of two or three connected vertices that could be cut off from the rest of the graph. As long as a graph with the correct degree numbers contains at least one edge from each of the cuts in the table below, the resulting graph will be connected.

vertices	cut
A, F	2, 3, 4, 5
C, D	7, 8, 9, 10
A, B, F	2, 5, 6, 8, 9
A, E, F	3, 4, 6, 7, 10
A, B	1, 2, 4, 6, 8, 9
B, C	3, 4, 6, 8, 10, 11
D, E	2, 5, 6, 8, 10, 11
E, F	1, 2, 4, 6, 7, 10
A, B, C	1, 2, 4, 6, 8, 10, 11

Avoiding rotations and reflections. Any valid graph can be rotated and reflected so that deg A = 1 or deg B = 1. By only considering graphs with deg A = 1 or deg B = 1, we will avoid double-counting all rotations and most reflections. If deg B = 1, it is still possible for two valid graphs to be horizontal reflections of one another. However, notice the edges are numbered so that i and j are horizontal reflections of one another if and only if i + j = 12. Using this property, we can easily identify those reflections.

The script I used is shown below. It declares a list for storing valid edge sets and defines functions for

counting the number of times each bridge appears in an edge set,
finding the degree of each vertex,
testing whether an edge set has a bridge crossing,
testing whether the graph corresponding to an edge set is connected, and
reflecting an edge set.

The script uses the combinations function from itertools to generate a list of all possible edge sets. In the main loop, each edge set and its reflection are compared to stored valid edge sets to make sure the edge set isn't a repeat. If an edge set is not a repeat, the degrees are computed. If the graph is in the correct orientation (i.e., if deg A = 1 or deg B = 1) and the degrees are 1, 2, 2, 3, 3, 3 and the edge set has no crossings and the corresponding graph is connected, then the edge set is stored as a valid edge set.

###############
# Definitions #
###############

# store valid edge sets to check for repeats and reflections
valid_edge_sets = list()

# return the number of times edge set e contains edge b
def c(e,b):
    return e.count(b)

# count incident edges to determine the degree of each vertex
def get_degrees(e):
    degA = c(e,1) + c(e,2) + c(e,3)
    degB = c(e,3) + c(e,4) + c(e,6) + c(e,8) + c(e,9)
    degC = c(e,9) + c(e,10) + c(e,11)
    degD = c(e,7) + c(e,8) + c(e,11)
    degE = c(e,2) + c(e,5) + c(e,6) + c(e,7) + c(e,10)
    degF = c(e,1) + c(e,4) + c(e,5)
    return [degA, degB, degC, degD, degE, degF]

# check if edge set e has crossing edges
def has_crossings(e):
    if (c(e,2) > 0 and c(e,4) > 0) or (c(e,8) > 0 and c(e,10) > 0):
        return True
    else:
        return False

# check cuts that would make the graph with edge set e disconnected, 
# return true if there's an edge across each of 9 possible cuts
def is_connected(e):
    connected = [0,0,0,0,0,0,0,0,0]
    if c(e,2) + c(e,3) + c(e,4) + c(e,5) > 0:
        connected[0] = 1
    if c(e,7) + c(e,8) + c(e,9) + c(e,10) > 0:
        connected[1] = 1
    if c(e,3) + c(e,4) + c(e,6) + c(e,7) + c(e,10) > 0:
        connected[2] = 1
    if c(e,2) + c(e,5) + c(e,6) + c(e,8) + c(e,9) > 0:
        connected[3] = 1
    if c(e,1) + c(e,2) + c(e,4) + c(e,6) + c(e,8) + c(e,9) > 0:
        connected[4] = 1
    if c(e,3) + c(e,4) + c(e,6) + c(e,8) + c(e,10) + c(e,11) > 0:
        connected[5] = 1
    if c(e,2) + c(e,5) + c(e,6) + c(e,8) + c(e,10) + c(e,11) > 0:
        connected[6] = 1
    if c(e,1) + c(e,2) + c(e,4) + c(e,6) + c(e,7) + c(e,10) > 0:
        connected[7] = 1
    if c(e,1) + c(e,2) + c(e,4) + c(e,6) + c(e,8) + c(e,10) + c(e,11)>0:
        connected[8] = 1
    if connected == [1,1,1,1,1,1,1,1,1]:
        return True
    else:
        return False

# reflect an edge set horizontally
def reflect(e):
    reflected_edges = list()
    for i in range(len(e)):
        reflected_edges.insert(0,12 - e[i])
    return tuple(reflected_edges)

# list all combinations of 7 edges from {1,1,2,2,...,11,11}
bridges = [1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10,11,11]
from itertools import combinations
edge_sets = list(combinations(bridges,7))

#############
# Main Loop #
#############

# find valid combinations in edge_sets
for e in edge_sets:
    # check if e is a repeat of another valid edge set
    if valid_edge_sets.count(e) + valid_edge_sets.count(reflect(e)) == 0:
        # compute the degree of each vertex
        degrees = get_degrees(e)
        degA = degrees[0]
        degB = degrees[1]
        degrees.sort()
        # check the orientation of the graph based on which vertex has 
        # degree 1, then check the degrees, crossings, and connectivity
        if (degA == 1 or degB == 1) and degrees == [1,2,2,3,3,3]:
            if not has_crossings(e) and is_connected(e):
                valid_edge_sets.append(e)
                print(e)

print("=======================")
print(len(valid_edge_sets), "edge sets")

@Thanos Petropoulos , we really liked your comment, and have converted it into a solution.

Brilliant Mathematics Staff - 1 year, 4 months ago

@Brilliant Mathematics , you accidentally posted my solution under Thanos's name.

Matt Janko - 1 year, 4 months ago

True, this is Matt's solution. I haven't posted my solution yet. Nice solution Matt!

Thanos Petropoulos - 1 year, 4 months ago

Pi Han Goh
Jun 5, 2015

First

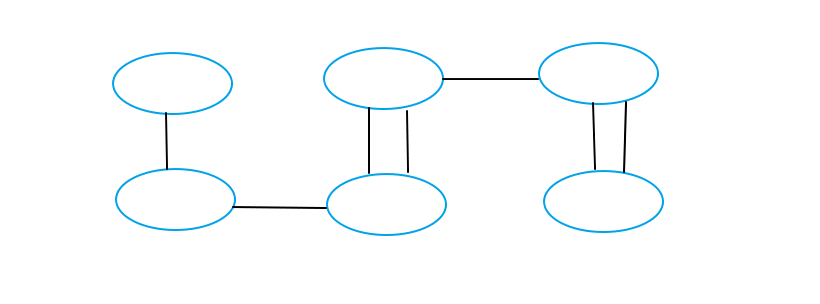
Second

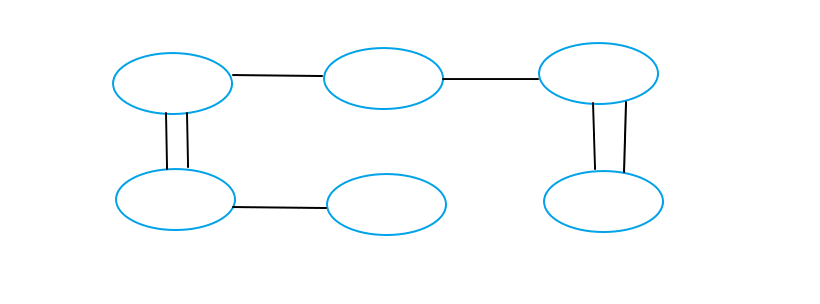
Third

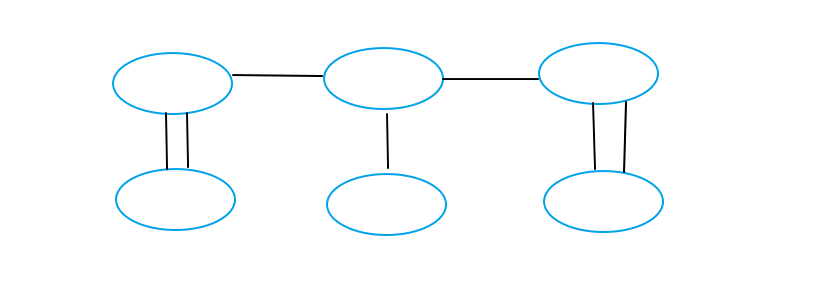
Fourth

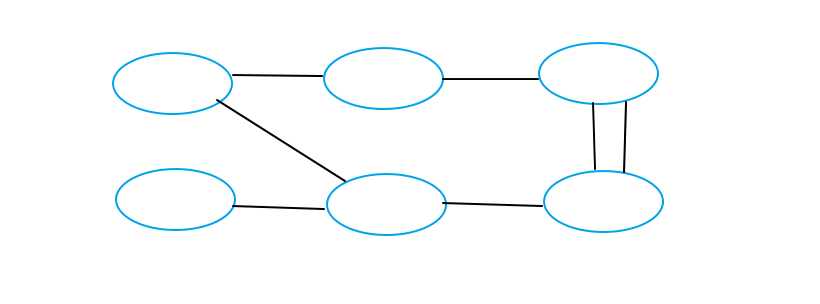
Fifth

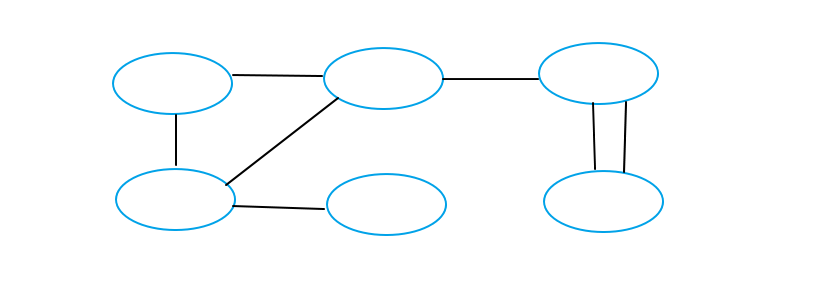
Sixth

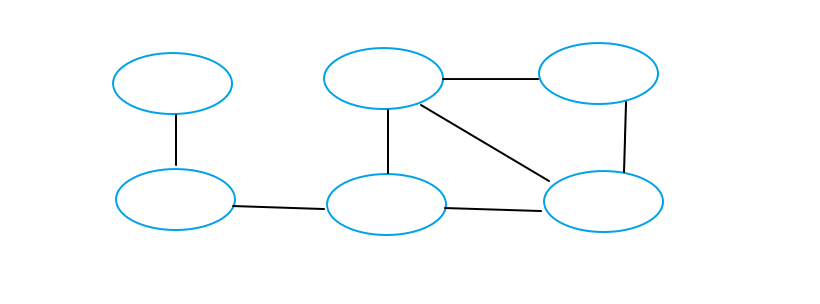
Seventh

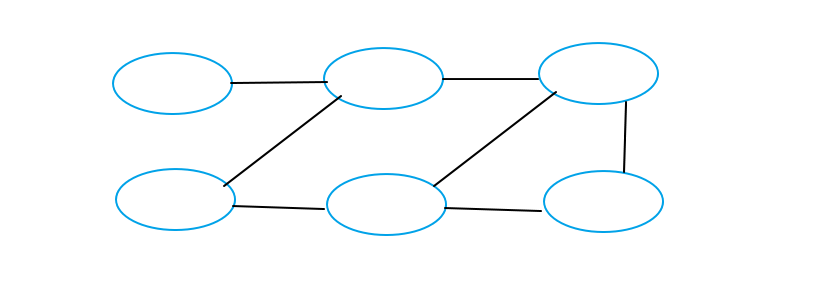
Eighth

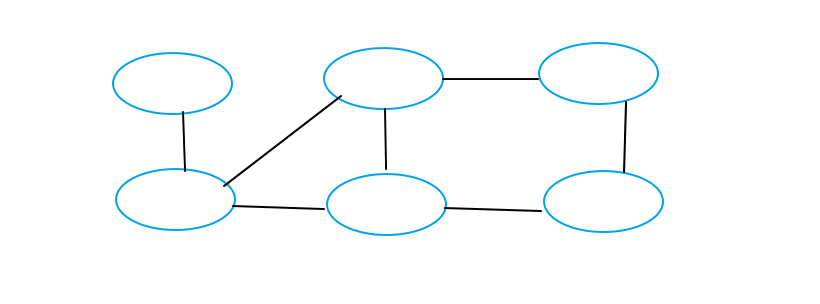
Ninth

Tenth

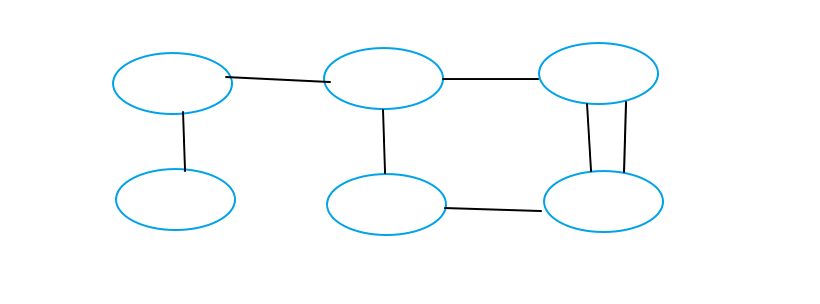
Eleventh

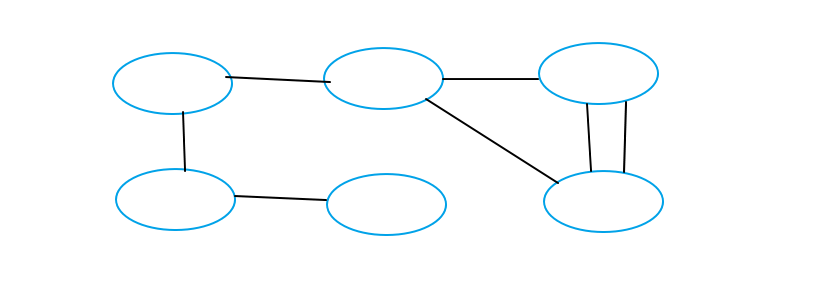
Twelfth

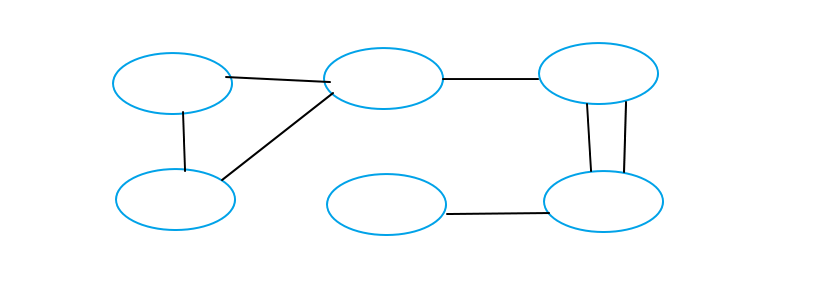
Moderator note:

How do you know that you have enumerated every single possibility?

After seeing your solution, the problem needs to be clarified
1. Islands on the left cannot be joined directly to islands on the right
2. We are allowed to build more than 1 bridge between 2 islands

Calvin Lin Staff - 6 years ago

the second term (the one about "more than one bridge between two islands") is absolutely NECESSARY in the initial text!

Nik Gibson - 2 years, 9 months ago

Is there any mathematical way for this

Department 8 - 5 years, 11 months ago

Challenge Master: I don't know. I assume Graph Theory is needed, but it's not my strong suit so I couldn't pinpoint what I should do next.

Pi Han Goh - 6 years ago

The problem description says "You cannot connect islands that are diagonally opposite". So, nine of your "solutions" are invalid by my interpretation of that constraint. Furthermore, I have an additional eight that you did not list (and these are not equivalent by rotation/reflection).

Here are my 12 configurations, without any diagonals: $\begin{array}{c|c|c|c} \begin{array}{ccccc} 1&-&2&-&3\\ & & & &\|\\ 2&=&3&-&3\\ \\ 1&-&3&=&3\\ & & & &|\\ 2&=&3&-&2\\ \\ 1&-&3&-&3\\ & &|& &\|\\ 2&=&3& &2 \end{array} & \begin{array}{ccccc} 1& &2&-&3\\ |& &|& &\|\\ 2&-&3&-&3\\ \\ 1& &3&=&3\\ |& &|& &|\\ 2& &3&-&2\\ \\ 1& &2&=&3\\ |& & & &|\\ 2&-&3&=&3\\ \\ 1& &3&=&3\\ |& &\|& &\|\\ 2&-&3& &2 \end{array} & \begin{array}{ccccc} 1& &2&-&3\\ |& &|& &\|\\ 3&=&3& &2\\ \\ 1& &2&=&3\\ |& & & &|\\ 3&=&3&-&2 \end{array} & \begin{array}{ccccc} 2&-&1& &2\\ |& & & &\|\\ 3&=&3&-&3\\ \\ 3&-&1& &2\\ \|& & & &\|\\ 3&-&2&-&3\\ \\ 2& &1& &2\\ \|& &|& &\|\\ 3&-&3&-&3 \end{array} \end{array}$

Tom Verhoeff - 4 years, 9 months ago

Oh I'm so sorry. I forgot how I formulated this question. If you don't mind, can you rephrase the question for me? Because I don't know how to fix it (even after reading your follow up comment in the report section).

And for some reason, I didn't get any notification from your message.

Pi Han Goh - 4 years, 9 months ago

@Pi Han Goh I think that the formulation where diagonal bridges are forbidden is fine. And I think that my diagram shows the 12 possible configurations (modulo rotation and reflection). So under Details and Assumptions add as second bullet point: "Diagonal bridges are not allowed."

Tom Verhoeff - 4 years, 9 months ago

@Tom Verhoeff – Thanks for your input. I have made the necessary editsss

Pi Han Goh - 4 years, 9 months ago

@Pi Han Goh – But you did not correct the answer :( It must be 12, not 13.

Babis Athineos - 3 years, 9 months ago

@Babis Athineos – Thanks. I've updated the answer to 12. Those who previously answered 12 has been marked correct.

Babis, in the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here .

Brilliant Mathematics Staff - 3 years, 6 months ago

But you said diagonal bridges are not permitted!

Fabricio Kolberg - 3 years, 6 months ago

Sorry, I've fixed the last line.

Pi Han Goh - 3 years, 6 months ago

But in that case, the thirteenth graph is also invalid :(

Fabricio Kolberg - 3 years, 6 months ago

@Fabricio Kolberg – I'm so sorry. I'll the admins take care of it. @Brilliant Mathematics , please change the answer to 12.

Pi Han Goh - 3 years, 6 months ago

@Pi Han Goh – Thanks. I've updated the answer to 12. Those who previously answered 12 has been marked correct.

Fabricio, in the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here .

Brilliant Mathematics Staff - 3 years, 6 months ago

Okay, I'm very confused - so long as diagonals are allowed (which the current phrasing says nothing about), there are WAY more than 12 distinct solutions. I found 53 distinct solutions personally, and I'm quite sure that they can't be simplified down to 12. I would list them, but that sounds exhausting.

Iain Lempke - 3 years, 2 months ago

Since you have 53 distinct solutions, can you list 1 or 2 of them that are different from what has been shown above?

I might be easier to check against the solutions listed by Tom below.

Calvin Lin Staff - 3 years, 2 months ago

Can it be solved this way? You put inside the circle (island) the number of bridges the island has. When you take two or more random solutions you can see that the sum of all numbers is always 14. Given digits 1,2,3 in two rows the only way to get 14 is sum of 7 in one row and 7 in the other one (7+7) or 8+6 or 9+5. Then you write down all of possibilities to get a sum of 7, 8, 6, 9 and 5 out of digits 1,2,3. Then you have to cross out all of the possibilities that would make a mirror image or 180-degree rotation. For example you can get a sum of 7 by adding 1,3,3 or 3,3,1 but we can see that 1,3,3 is a mirror image of 3,3,1 so for the porpoise of this task it is the same. When you cross out all of the unnecesery possibilities you are left with 4 ways to connect the islands using the sum 7+7, 2 ways using 9+5 and 6 ways using 8+6, so all together 12 ☺ Please let me know if this is correct

Sylawi Silibee - 2 years, 8 months ago

3,3,3 on the top and 1,2,2, with a double bridge between the right and centre 3s (and the rest filled in accordingly) is a valid configuration which isn't on the list - please update this question with some kind of analytic answer

Chris Purdy - 1 year, 6 months ago

Connecting Isles

Adapted from a Puzzle book.

The answer is 71.

2 solutions

Moderator note:

1 pending report

Vote up reports you agree with