Constant Distance Ratio Sphere
Two points A and B in 3-dimensional space have the following coordinates: A = ( 2 , 1 , 3 ) , B = ( 1 0 , 1 0 , 1 5 ) . The locus of all the points P = ( x , y , z ) that have the property that P B P A = 2 is a sphere.
Find its radius to 2 decimal places.
The answer is 11.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
When you complete the squares, remember that (b/2)^2 must be added, not b. So, I believe your conclusion is wrong.
Incidentally, I arrived at the answer 85/6 = 14.1667 by a much simpler approach. If we extend a line through the two points, we see that it must pass through the center of the sphere. The distance between the points is 17. If we draw a number line on this, with 0 at A and 17 at B, then the points 17/3 and 34 are on the sphere. The diameter is then 34 - 17/3 = 85/3. Therefore, the radius is 85/6.
Log in to reply
I too thought of this solution. But I could not prove easily "If we extend a line through the two points, we see that it must pass through the center of the sphere." I think it needs a proof.
What I thought is this.
Since the given line is used in generating a sphere, it must be line of symmetry with reference to the sphere. So it must be colinear with a diameter of a great circle in any plain containing the line. Then your solution is perfect.
There is another point. Since the radius of great circle and that of the sphere is the same, we have simplified a 3-D problem to 2-D.
Up voted. It is the solution from the basic, which all can understand. Though the problem says that the locus is a sphere it is an additional data. You have proved without this data.
Nice derivation 1 1 5 6 = 3 4
Tom Engelsman offers a proof of why it's a sphere. But if we assume it must be a sphere, then if
P
is where it passes through the line between
A
and
B
, and
Q
is where it passes through the line outside of the segment
A
B
=
1
7
, then we know that
A
P
=
3
1
7
, and
A
Q
=
1
7
.
The radius is
2
1
of
A
P
+
A
Q
=
3
3
4
=
1
1
.
3
3
3
.
.
.
Obviously 1 : 2 = ( 3 1 7 ) : ( 3 3 4 ) = ( A P ) ( A B − A P ) and 1 : 2 = ( 1 7 ) : ( 3 4 ) = ( A Q ) : ( A B + A Q )
This is the approach I took... :)
We are given that,
P A = k P B , k > 0
So, in terms of the vectors P , A , and B , this becomes,
( P − A ) T ( P − A ) = k 2 ( P − B ) T ( P − B )
Expanding,
P T P − 2 A T P + A T A = k 2 ( P T P − 2 B T P + B T B )
Rearranging,
( k 2 − 1 ) P T P + 2 ( A − k 2 B ) T P + k 2 B T B − A T A = 0
Define P 0 = − k 2 − 1 1 ( A − k 2 B ) , then
( k 2 − 1 ) ( P − P 0 ) T ( P − P 0 ) = A T A − k 2 B T B + ( k 2 − 1 ) P 0 T P 0
Now,
P 0 T P 0 = ( k 2 − 1 ) 2 1 ( A T A + k 4 B T B − 2 k 2 A T B )
Therefore,
( k 2 − 1 ) ( P − P 0 ) T ( P − P 0 ) = A T A − k 2 B T B + k 2 − 1 1 ( A t A + k 4 B T B − 2 k 2 A T B ) = k 2 − 1 1 { ( k 2 − 1 ) A T A − k 2 ( k 2 − 1 ) B T B + A T A + k 4 B T B − 2 k 2 A T B } = k 2 − 1 1 ( k 2 A T A + k 2 B T B − 2 k 2 A T B ) = k 2 − 1 k 2 ( A − B ) T ( A − B ) Hence,
( P − P 0 ) T ( P − P 0 ) = ( k 2 − 1 k ) 2 ( A − B ) T ( A − B ) = r 2
This is an equation of a sphere with center P 0 and radius r , where
P 0 = k 2 − 1 1 ( k 2 B − A )
and,
r = ∣ k 2 − 1 k ∣ ∣ A − B ∣
Substituting k = 2 , and A = ( 2 , 1 , 3 ) and B = ( 1 0 , 1 0 , 1 5 ) , we obtain
r = ∣ 2 2 − 1 2 ∣ ∣ ( 2 , 1 , 3 ) − ( 1 0 , 1 0 , 1 5 ) ∣ = 3 2 ∣ ( − 8 , − 9 , − 1 2 ) ∣ = 3 2 ( 1 7 ) = 3 3 4 = 1 1 . 3 3 .
Great! That's the generalized version of Appolonius circles , namely that the set of points P which satisfy P B P A = k in R k is a k − sphere.
The calculations are identical to what you did, in k − dimensions.
By symmetry, the center of the sphere has to be on the line connecting A and B.
On this line we can identify two points that have PA =2PB:
- one is between A and B, where PA = 2/3 AB and PB = 1/3 AB
- one is 'past B', as seen from A, where PA = 2AB and PB = AB
So these two points are 4/3 AB apart, so our radius must be r = 3 2 A B = 3 2 8 2 + 9 2 + 1 2 2 = 3 3 4 = 1 1 . 3 3 3 . . . .
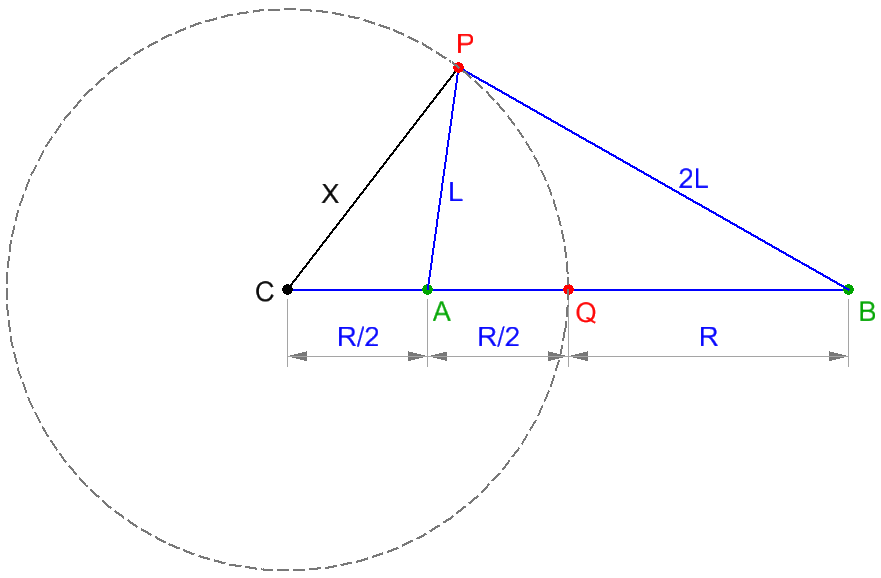
This locus of points at distances 1:2 from two fixed points, is a known way of defining a circle as well. The radius of the circle is 2/3 the distance between the two fixed points. So the radius will be (Distance 17) x 2 / 3 = 11.33
(Sorry, IMGUR is temporarily down, i will upload the image when it allows me to log in)
Here is a proof of this result:
Consider a circle of radius R and center C. Points A & B lie on a radial line at a distance R/2 and R from the point Q on the circle.
Now take a point P at an arbitrary distance L from A and 2L from B. Let CP = x.
Let's check if point P lies on the circle, using Stewart's theorem in the triangle shown:
2 3 R × 2 R × 2 R + 2 R × L 2 = X 2 × 2 3 R + 4 L 2 2 R
which gives X = R i.e. for any arbitrary distance L, point P always lies at a distance R from the center C, thus tracing the circle.
Rather then 1:2 ratio, it can be any fixed ratio, say m:n, n>m>0. I think then
r=Distance * n/(m+n). Can you please provide the source of this information? Thanks.
Log in to reply
wow! That is a powerful generalization. I remember the 1:2 result from the problems on 'Locus' in XI grade textbook.
Log in to reply
I was wrong. The correct expression is as under.
G
i
v
e
n
r
a
t
i
o
=
m
n
,
n
>
m
>
0
.
r
=
(
l
e
n
g
t
h
o
f
t
h
e
l
i
n
e
)
∗
n
2
−
m
2
m
∗
n
.
O
R
G
i
v
e
n
r
a
t
i
o
=
k
>
1
.
r
=
(
l
e
n
g
t
h
o
f
t
h
e
l
i
n
e
)
∗
k
2
−
1
k
.
a
s
g
i
v
e
n
b
y
M
r
.
H
o
s
a
m
H
a
j
j
i
r
.
I
s
a
w
i
t
o
n
l
y
n
o
w
!
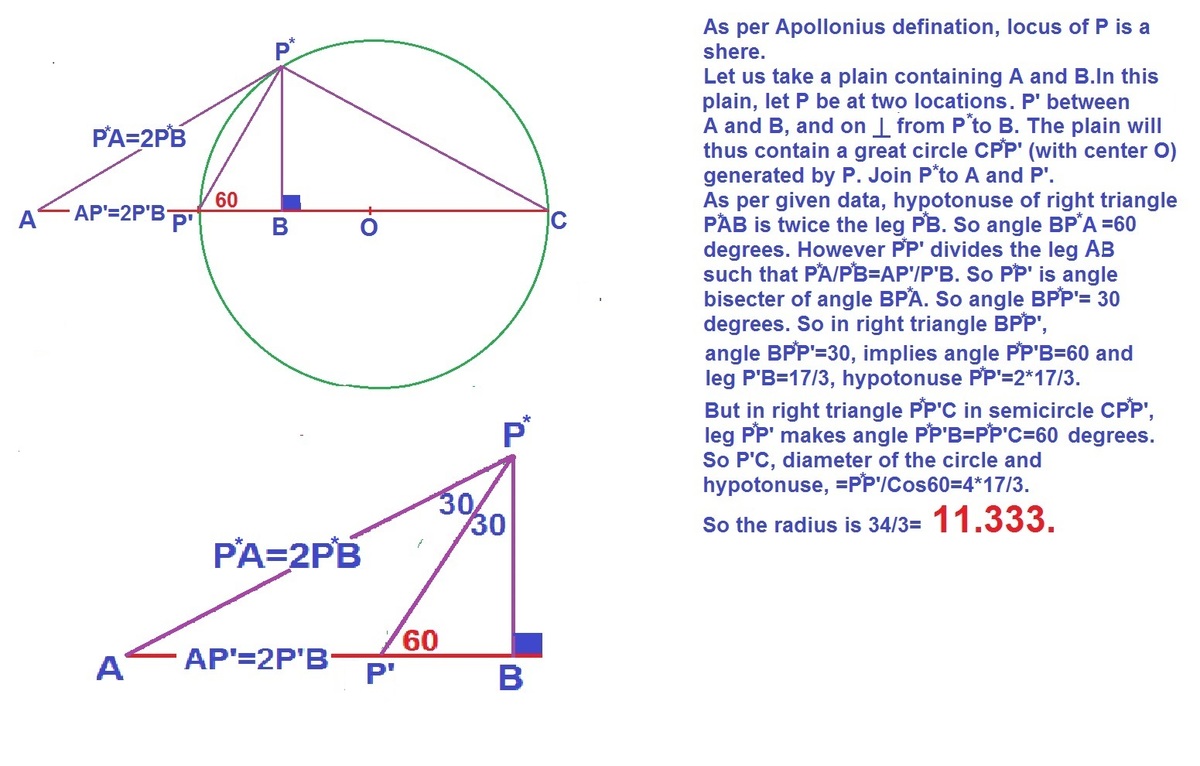
Sir, I have added a proof above for the 1:2 result I used.Could not upload the figure on IMGUR, due to some error on the site. i will try again later. But the description should work without it too.
Log in to reply
Thank you for the proof. I am trying to give proof for the general case.
Copy Your computer file. Down load it in any old solution file of your Brilliant folio. Copy it from there and down load in your comment. Delete it from the old file. No need of IMGUR!!!
Log in to reply
@Niranjan Khanderia – Sorry, I completely overlooked the 'attach image' button! Was still using the old IMGUR route. The figure is now attached.
Let's take ( x − 2 ) 2 + ( y − 1 ) 2 + ( z − 3 ) 2 = 2 ( x − 1 0 ) 2 + ( y − 1 0 ) 2 + ( z − 1 5 ) 2 ;
or ( x − 2 ) 2 + ( y − 1 ) 2 + ( z − 3 ) 2 = 4 [ ( x − 1 0 ) 2 + ( y − 1 0 ) 2 + ( z − 1 5 ) 2 ] ;
or ( x 2 − 4 x + 4 ) + ( y 2 − 2 y + 1 ) + ( z 2 − 6 z + 9 ) = 4 [ ( x 2 − 2 0 x + 1 0 0 ) + ( y 2 − 2 0 y + 1 0 0 ) + ( z 2 − 3 0 z + 2 2 5 ) ;
or 1 4 = 3 x 2 + 3 y 2 + 3 z 2 − ( 8 0 − 4 ) x − ( 8 0 − 2 ) y − ( 1 2 0 − 6 ) z + 1 7 0 0 ;
or 1 4 − 1 7 0 0 = ( 3 x 2 − 7 6 x ) + ( 3 y 2 − 7 8 y ) + ( 3 z 2 − 1 1 4 z ) ;
or − 1 6 8 6 = 3 ( x 2 − 3 7 6 x ) + 3 ( y 2 − 2 6 y ) + 3 ( z 2 − 3 8 z ) ;
or − 3 1 6 8 6 = ( x 2 − 3 3 8 x + ( 3 3 8 ) 2 − ( 3 3 8 ) 2 ) + ( y 2 − 1 3 y + 1 6 9 − 1 6 9 ) + ( z 2 − 1 9 z + 3 6 1 − 3 6 1 ) ;
or − 3 1 6 8 6 + ( 3 3 8 ) 2 + 1 6 9 + 3 6 1 = ( x − 3 3 8 ) 2 + ( y − 1 3 ) 2 + ( z − 1 9 ) 2 ;
or 9 1 1 5 6 = ( x − 3 3 8 ) 2 + ( y − 1 3 ) 2 + ( z − 1 9 ) 2 ;
Thus, the locus is a sphere centered at ( 3 3 8 , 1 3 , 1 9 ) and with radius 9 1 1 5 6 ≈ 1 1 . 3 3 .