Constructing a tetrahedron
For this problem, we will define a "unit polyhedron" to be a polyhedron of edge length one.
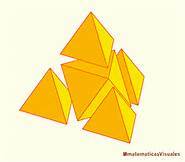
The picture to the right shows how a larger tetrahedron can be built from four unit tetrahedra and one unit octahedron.
Amanda wishes to construct a much larger tetrahedron with many more unit tetrahedra and octahedra. In the end, she builds one using exactly 364 unit octahedra and some unit tetrahedra.
How many unit tetrahedra did she use?
Assumption: The final construction is one solid tetrahedron, with nothing extra sticking out, and nothing missing (no holes). No unit octahedra or tetrahedra are cut in any way.
Image credit: http://www.matematicasvisuales.com/
The answer is 741.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
To make tetrahedra of linear size n , you need
- 6 1 n ( n 2 − 1 ) octahedra
- 3 1 n ( n 2 + 2 ) tetrahedra
Got a proof?
Log in to reply
Let me see if I can find my original derivation...
There... I've added a derivation to the solution. What do you think?
Log in to reply
Well, you seem to be missing out in a lot of steps here
These recurrence relations translate into:
- O n = 6 1 n ( n 2 − 1 )
- T n = 3 1 n ( n 2 + 2 )
But overall, it looks good! Thankss
Log in to reply
@Pi Han Goh – Thanks for the feedback... When I get a chance, perhaps I'll try to fill in the missing steps...
The formulae for constructing the tetrahedron (thanks Michael Mendrin for providing these!) are as follows:
To make tetrahedra of linear size n , you need
These equations can be derived as follows:
===========================================
Consider the triangular numbers, Δ n = 2 n ( n + 1 )
Also, lets consider ( O n , T n ) for the number of octahedra and tetrehedra in a "great tetrahedra" of linear dimension, n . Clearly for n = 1 and n = 2 we have:
(The second equation being the picture in the problem)
The thing to notice here, is that each time we add a row of tetrahedra and octahedra to construct the next "great tetrahedra" with one more linear dimension, we add Δ n − 1 octahedra and Δ n + Δ n − 2 tetrahedra.
So, for n>2
These recurrence relations translate into:
===========================================
The first equation gives us 3 6 4 octahedra for n = 1 3 .
So, for n = 1 3 the second equation gives us that there are 7 4 1 tetrahedra.