Continued Matrices
If [ 1 1 1 0 ] k = [ a k c k b k d k ] , find the closed form of k → ∞ lim c k a k to 3 decimal places.
The answer is 1.618.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Interesting observations made here!
Solution 1 could be improved by explaining how and why the Fibonacci numbers appear in the pattern.
Similarly, solution 2 should clarify that the first line is a "known fact", especially if you do not intend to prove it. Note that solution 2 doesn't prove yet that lim c k a k is equal to the infinite continued fraction. There is a slight gap in the rigor.
The infinite continued fraction will equal the golden ratio provided that the finite approximants converge to this value; and they do. This is easy to prove from the Binet formula for Fibonacci numbers and the fact that each approximant is a ratio of of consecutive Fibonacci numbers.
Relevant wiki: Fast Fibonacci Transform
Let A k = [ 1 1 1 0 ] k . With matrix multiplication, we can see that A 1 = [ 1 1 1 0 ] , A 2 = [ 2 1 1 0 ] , A 3 = [ 3 2 2 1 ] , A 4 = [ 5 3 3 2 ] , A 5 = [ 8 5 5 3 ] . Looking at the coefficients of each of elements suggests that they follow a Fibonacci sequence .
Claim: [ 1 1 1 0 ] n = [ F n + 1 F n F n F n − 1 ] .
Proof:
This statement is obviously true for F 0 , F 1 , and F 2 since
[ 1 1 1 0 ] 1 = [ F 2 F 1 F 1 F 0 ] .
Assume that it also holds for some k , then we have
[ 1 1 1 0 ] k = [ F k + 1 F k F k F k − 1 ] .
Now, multiplying both sides with [ 1 1 1 0 ] , we have
[ 1 1 1 0 ] k + 1 = [ F k + F k + 1 F k + 1 F k + 1 F k ] .
This implies
[ 1 1 1 0 ] k + 1 = [ F k + 2 F k + 1 F k + 1 F k ] ,
which follows from the definition.
Hence, the identity holds for any n . QED
Our answer is k → ∞ lim c k a k = k → ∞ lim F k + 1 F k + 2 = ϕ ≈ 1 . 6 1 8 , where ϕ denotes the golden ratio .
calculating this was trivial, I saw the solution immediately
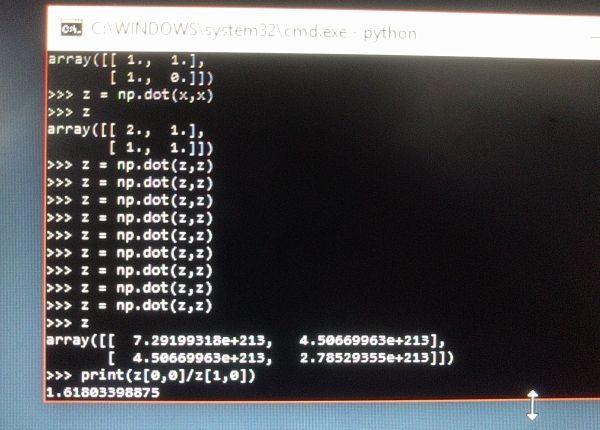
This is wrong, you have only calculated the value of c 1 0 2 4 a 1 0 2 4 . The question asked to calculate n → ∞ lim c n a n .
Log in to reply
It's even better because it's a scalable solution, you could just keep doing it to get a more accurate answer. The question also states that only 3 decimals of accuracy are required.
Log in to reply
That's wrong. You first need to show that the limit, n → ∞ lim c n a n exists, then show that ∣ ∣ ∣ ∣ c 1 0 2 4 a 1 0 2 4 − n → ∞ lim c n a n ∣ ∣ ∣ ∣ < 1 0 − 3 .
Log in to reply
@Pi Han Goh – It's not wrong, and it's frivolous showing that but okay. We can assume lim n → ∞ c n a n ≈ 1 . 6 1 8 because that is the answer to the question, and in my screenshot you can see that lim n → ∞ c 1 0 2 4 a 1 0 2 4 ≈ 1 . 6 1 8 0 3 3 9 8 8 7 . From there it's trivial to subtract 1 . 6 1 8 from 1 . 6 1 8 0 3 3 9 8 8 7 to get 0 . 0 0 0 0 3 3 9 8 8 7 and ∣ 0 . 0 0 0 0 3 3 9 8 8 7 ∣ < 1 0 − 3
Log in to reply
@Kyle Gray – By your logic, n → ∞ lim ( − 1 ) n = ( − 1 ) 1 0 0 0 0 0 0 0 0 0 0 0 0 = 1 because we can assume that lim n → ∞ ( − 1 ) n ≈ 1 . 0 0 0 0 0 because that is the answer to whatever question you're speaking of.
Log in to reply
@Pi Han Goh – Maybe you just don't understand, but that's okay. If the answer to the question was 1 then by definition it must equal 1.
Solution 1:
[ 1 1 1 0 ] n = [ F n + 1 F n F n F n − 1 ]
lim n → ∞ F n F n + 1 = Φ ≈ 1 . 6 1 8
Solution 2:
∏ i = 0 n [ a i 1 1 0 ] = [ p n q n p n − 1 q n − 1 ] ⇔ q n p n = [ a 0 , a 1 , a 2 , . . . , a n ]
Consider the infinite continued fraction
[ 1 , 1 , 1 , 1 , 1 , . . . ] = 1 + 1 + 1 + 1 + ⋱ 1 1 1 1
x = 1 + 1 + 1 + 1 + ⋱ 1 1 1 1
x = 1 + x 1
x 2 − x − 1 = 0
x = 2 1 ± 5
but because we are adding, our solution is
x = 2 1 + 5 = Φ = 1 . 1 6 1 8 . . .
now because
lim n → ∞ q n p n = [ 1 , 1 , 1 , 1 , . . . ] = Φ
and
[ 1 1 1 0 ] k = [ a k c k b k d k ]
then
lim k → ∞ c k a k = Φ ≈ 1 . 6 1 8