Continuity check
m is a positive integer such that
f ( x ) = k = 1 ∑ ∞ ( 1 + x 4 ) k − 1 x m .
Given that f ( x ) is continuous at x = 0 , find the smallest possible value of m .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Could you just tell me why did you write
If x = 0 , f ( 0 ) = 0 ?
I mean it is only mentioned that f ( x ) is continuous at x = 0 . Nothing has been said about the value at x = 0 .
Log in to reply
Because, when x=0 all the terms are 0. x m in the numerator.
Ur right.nothing is said about the value at x=0....but when x=5 I have the expression as x+x^5 and as we check in the left of zero we have negative value and at right it positive.....this should not be there as the function is continuous at x=0.. . I think that the answer is 4
Log in to reply
We can have a continuous function that is positive on one side and negative on the other. It is a necessary condition that the value at that point is 0.
Explicitly, here is the graph of this function when m = 5 .
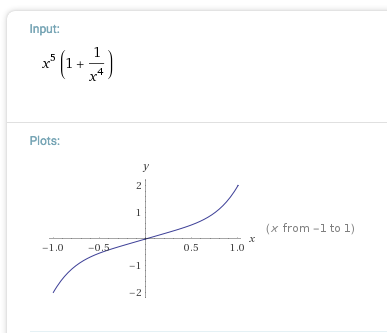
I think the answer must be 'smallest integer value of m'.
What is wrong with m = 4? @Calvin Lin @Jin Young Hwang
Log in to reply
Same is my question. :(
Log in to reply
When m = 4 , is the function continuous at x = 0 ?
Hint: Notice that f ( 0 ) = 0 , as stated in the solution.
If x = 0 , f ( x ) is a geometric series whose first term is x m , and common ratio 1 + x 4 1 < 1 . Therefore, f ( x ) = 1 − 1 + x 4 1 x m = x 4 x m ( 1 + x 4 ) = x m ( 1 + 1 / x 4 ) .
If x = 0 , f ( 0 ) = 0 .
∴ f ( x ) = { x m ( 1 + 1 / x 4 ) 0 i f x = 0 i f x = 0
Since f is continuous at x = 0 , x → 0 lim x m ( 1 + 1 / x 4 ) = 0 . If 1 ≤ m ≤ 3 , the limit doesn't exist. If m = 4 , the limit is 1. If m ≥ 5 , the limit is 0 and we get the answer.