Converting rectangle to hexagon
True, False, or Conditionally True?
We can cut any rectangle into three pieces using straight lines, and rearrange these pieces into a convex hexagon whose sides are all of the same length.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Notice that the final equation is equivalent to X 2 = 4 S 2 + ( L − X ) 2 , or that X = 8 L 4 L 2 + S 2 .
But because we also need X < L (implied constraint in the diagram), hence this gives us S 2 < 4 L 2 , or that S < 2 L like in Marta's analysis.
If the short and long sides of the rectangle are s and l, and the length of the black lines is x, it is not too hard to show that 4 s 2 + ( l − x ) 2 = x 2 which is easily solved for x.
Log in to reply
I am not really following. Can you please explain?
Log in to reply
He is claiming that, given the sides of the rectangle s and l, you can always find a value x that corresponds to where in the picture the 3 lines meet. (Though he does not prove that x is always less than l)
Log in to reply
@Alex Li – Yes, you can always find a solution. If the condition failed, just replace L by S and S by L or rotate the rectangle 90 degrees.
Log in to reply
@Ossama Ismail – I see that you added a figure to explain this. That is great!
How can you be sure that you can actually find such black lines?
Log in to reply
I agree, the solution writer only shown that it's true for 2 configurations, but he didn't show that it's true for all possible configurations.
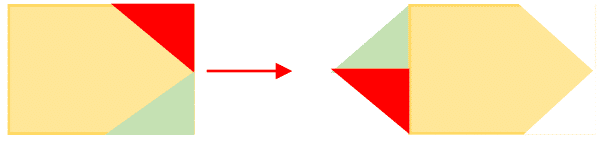To construct the solution, we proceed as shown below.
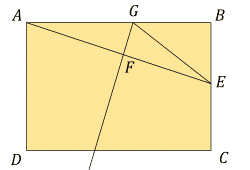
Make E is a midpoint of the shorter side (or midpoint of any side if A B C D is a square). Find midpoint F of A E . Draw a line perpendicular to A E through F . G is an intersection of this line with A B . This construction guarantees that A G = G E . Cut along G E , and symmetrically below. Move pieces as shown above.
The construction will fail, that is the line through F will not intersect the segment A B , only if B C > 2 A B or it is equal to it. Since we picked the smaller of the two sides (or one of the sides of a square), this cannot happen.
First of all, I thought that I have to come up with a regular Hexagon. So I hit false. Because otherwise I would have known is true. The hypothesis didn't state that the second form is just a guide.
Log in to reply
I do not think it is necessary to state that the second form is just a guide. Pictures are always guides. Somebody said, "Geometry is the art of making correct statements by looking at wrong figures."
Log in to reply
True, but I agree that making that image a bit less regular would have been probably fair. It's okay to not give away the solution, but actually misleading is less recommended.
Log in to reply
@Marta Reece – I don't understand. Doesn't the problem ask for regular hexagon? Why do we want to make it less regular?
Log in to reply
@Christopher Boo – The problem asks for a hexagon with equal sides. The solution has equal sides but not equal angles. So it is not a regular hexagon. What we could do is make the image less regular in a similar way.
Log in to reply
@Marta Reece – Oh right, what was I thinking. Thanks for the clarification!
No, remember that all sides of the hexagon must have the same length.
Log in to reply
I have modified the image to satisfy that requirement and added section explaining how the requirement is satisfied.
The line through F has to be perpendicular to AE, not AB
Log in to reply
I made the correction. Sorry about not catching it before and thanks for pointing it out.
I have understood that sides of the exagon had to be pieces of the border of the rectangle, the figure could be full of color to be more clear.
Answer: Yes ..
Note:: all black lines have the same length.
Assume the length of the black line = X and the rectangle dimensions are S and L .
To find X , solve X = 4 S 2 + ( L − X ) 2