Cool bisector
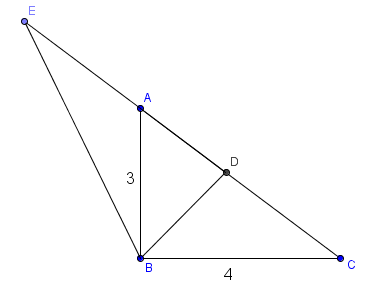
In △ A B C , ∠ B = 9 0 ∘ , A B = 3 , and B C = 4 .
B D is the bisector of ∠ A B C , and E A = B D .
Find the area of △ E A B .
The answer is 2.91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I'm getting a different answer, although it was close enough to be considered correct.
First, by similarity, we have that 5 3 = 4 ∣ B D ∣ ⟹ ∣ B D ∣ = 5 1 2 .
Next, we have that the area of Δ E A B is
2 1 ( ∣ A B ∣ ) ( ∣ E A ∣ ) sin ( ∠ B A C ) = 2 1 ( 3 ) ( 5 1 2 ) ( 5 4 ) = 2 5 7 2 = 2 . 8 8 .
Log in to reply
∠ A D B is not 9 0 ° maybe this was the little mistake
Log in to reply
Ah, o.k., my mistake. That makes the problem more difficult. I'm lucky it was close to 9 0 ∘ so that my answer was close enough to 2 . 9 1 to be accepted as "correct", even though my approach was wrong. Nice problem. :)
Log in to reply
@Brian Charlesworth – Excuse me sir! , I misunderstand the comment. I do not consider someone were to make a solution for similarity, maybe I was neglected with this kind of solutions
Log in to reply
@Paola Ramírez – Your approach is correct, and mine is incorrect, but the way it works with real-valued answers on Brilliant is that if one's answer is within a certain percentage of the posted answer then it is given credit as being "correct", even if the method used was flawed. So in this case I was just fortunate, that's all. What might have worked better is to have asked at the end something like, "if the area of Δ E A B = c a b , where a , c are coprime and b is square-free, then find a + b + c . " Then the answer would be 1 0 9 , and an approach like mine, i.e., based on a wrong assumption, would not then have yielded a solution that was considered correct.
@Brian Charlesworth – Hey its not ur mistake.the answer is exactly 2.88 and not 2.91. Becoz its the property of similar triangles that by default angle BDA will be 90..as AD is an angular bisector of angle BAC..
Log in to reply
@Rajath Naik – Paola is correct; ∠ B D A is not a right angle. It is actually
1 8 0 ∘ − 4 5 ∘ − arctan ( 3 4 ) = 8 1 . 8 7 ∘
to 2 decimal places, which is quite far off being a right angle, but because sin ( 8 1 . 8 7 ∘ ) = 0 . 9 9 to 2 decimal places, i.e., very close to 1 , when the area calculation is made the answer using my incorrect method ended up being nearly identical to Paola's exact value.
Log in to reply
@Brian Charlesworth – Well thanks..I guess I was wrong then, gotta rethink.
@Rajath Naik – If B D A = 9 0 then , Δ A B C will be a 45 - 45 - 90 triangle , which is a special case.
Nice👍👍👏👏😊😊
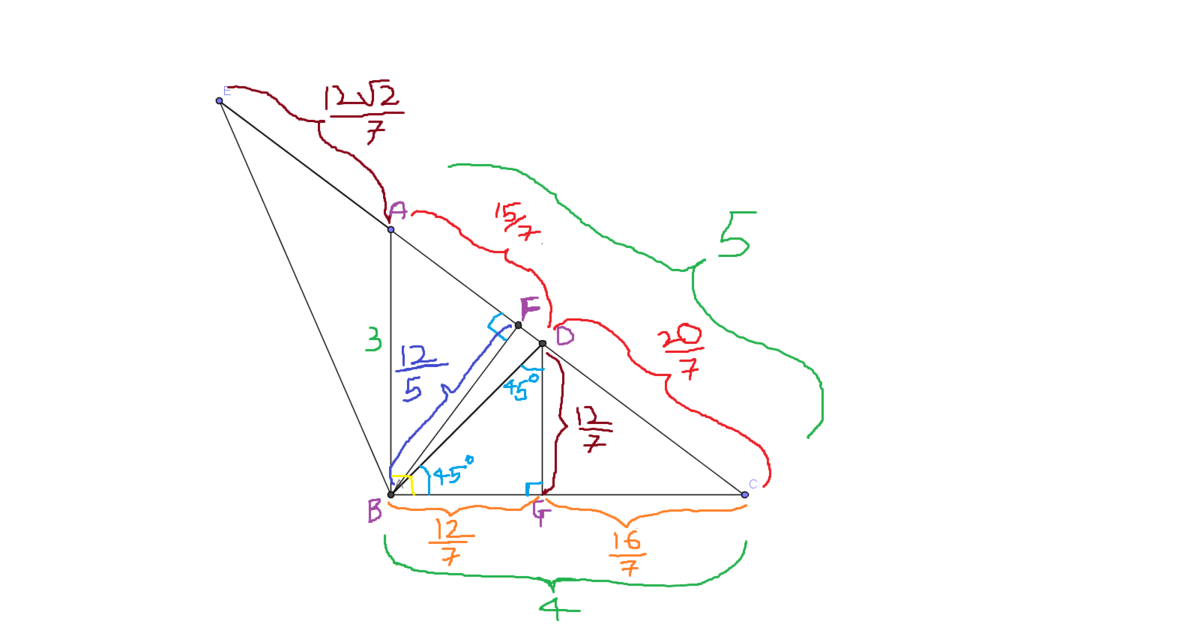
All I did was B F ⊥ A C a n d D G ⊥ B C
Thus [ E A B ] = 2 ( A E ) ( B F ) = 2 ( 7 1 2 2 ) ( 5 1 2 ) = 3 5 7 2 2 ≈ 2 . 9 0 9 ≈ 2 . 9 1
Great answer 👏
I have no idea how sines work so I used this to get 2.88:
I assumed angle B D A was a right angle. With the pythagorean theorem, we get a 2 + b 2 = c 2 Substituting... ( 3 ) 2 + ( 4 ) 2 = c 2 , 9 + 1 6 = c 2 , 2 5 = c 2 , 5 = c
Area of Δ A B C = 2 ( 3 ) ( 4 ) = 6
Let's call the length of line B D ′ x ′ . Then 2 5 x = 6 ... x = ( 1 2 / 5 ) = 2 . 4
Now, since we know that E A = B D , E A = 2 . 4 . I'll call the length of line E A ′ y ′ .
And finally, we find the area of Δ E B C + Δ A B C : 2 ( 5 + y ) ( 2 . 4 ) = 2 ( 5 + ( 2 . 4 ) ) ( 2 . 4 ) = 2 ( 7 . 4 ) ( 2 . 4 ) = 2 1 7 . 7 6 = 8 . 8 8
Subtract the area of Δ A B C for Δ E A B :
8 . 8 8 − 6 = 2 . 8 8
l e t x = A D a n d y = D C . α = ∠ B D A , B F ⊥ A C , F o n A C . 3 2 + 4 2 = 5 = A C = x + y . B i s e c t o r T h e o r e m : − 3 x = 4 y = 4 5 − x , ∴ x = 7 1 5 , a n d y = 5 − x = 7 2 0 . B F = 3 ∗ S i n B A C = 3 ∗ 5 4 = 5 1 2 . A E = B D = 3 ∗ 4 − x ∗ y = 1 2 − 4 9 3 0 0 A r e a Δ E A B = 2 1 ∗ A E ∗ B F = 2 . 9 0 9
l e t x = A D a n d y = D C . α = ∠ B D A 3 2 + 4 2 = 5 = A C = x + y . A p p . S i n e R u l e : − S i n 4 5 x = S i n α 3 , S i n 4 5 y = S i n ( 1 8 0 − α ) 4 . A d d i n g t h e t w o e q u a t i o n s S i n α = 5 ∗ 2 7 . A p p . S i n e R u l e : − S i n 4 5 x = S i n α 3 , ∴ x = 7 1 5 , a n d y = 5 − x = 7 2 0 . B i s e c t o r T h e o r e m : − A E = B D = 3 ∗ 4 − x ∗ y = 1 2 − 4 9 3 0 0 . L e t B F ⊥ A C N o t e : − B F ⊥ A C , B A : A F : B F : : 5 : 3 : 4 I n r t . ∠ d Δ A B C , B F ⊥ A C , ⟹ B F ⊥ E A , = 5 3 ∗ 4 = 5 1 2 . A r e a Δ E A B = 2 1 ∗ A E ∗ B F = 2 . 9 0 9
l e t x = A D a n d y = D C . α = ∠ B D A , B F ⊥ A C , F o n A C . 3 2 + 4 2 = 5 = A C = x + y . B i s e c t o r T h e o r e m : − 3 x = 4 y = 4 5 − x , ∴ x = 7 1 5 , a n d y = 5 − x = 7 2 0 . B F = 3 ∗ S i n B A C = 3 ∗ 5 4 = 5 1 2 . A E = B D = 3 ∗ 4 − x ∗ y = 1 2 − 4 9 3 0 0 A r e a Δ E A B = 2 1 ∗ A E ∗ B F = 2 . 9 0 9
I used the angle bisector theorem and triangle similarity. I extended line BA and drew a line from point E such that it is perpendicular to extended line BA. Let the point of intersection of those two aforementioned lines be X. To find the area, we are already given the "base" of triangle EAB, which is 3, so we just need the value of line EX. We already know that via pythagorean theorem, AC= 5.Use x a = y b and the previous information to obtain the values of AD and DC (system of equations).Then plug into e 2 = a b − x y to get e (which is DB). Since DB=EA, use triangle similarity to obtain the value of EX. Then use area of triangle to get the final answer.
It seems that some other parameter must be assigned a value.
Log in to reply
What's a rentangle?
Log in to reply
she means that Δ A B C is right angled at ∠ B . So essentially a "rectangular" triangle is a right triangle.
Log in to reply
@Brian Charlesworth – Then you were correct with your first solution?
Log in to reply
@Guiseppi Butel – No, I was mistaken; I didn't read the question carefully the first time. Since B D is a bisector of ∠ B we have ∠ A B D = 4 5 ∘ , but since ∠ B A D = arctan ( 3 4 ) = 5 3 . 1 3 ∘ we end up with ∠ B D A = 1 3 5 ∘ − arctan ( 3 4 ) = 8 1 . 8 7 ∘ , i.e., not a right angle. From here, using the Sine law, we would then have
∣ A B ∣ sin ( ∠ B D A ) = ∣ B D ∣ sin ( ∠ B A D )
⟹ ∣ B D ∣ = sin ( 1 3 5 ∘ − arctan ( 3 4 ) ) 3 ∗ sin ( arctan ( 3 4 ) ) = 7 1 2 ∗ 2 3 ∗ 5 4 = 7 1 2 2 .
So using this value for ∣ E A ∣ = ∣ B D ∣ , the area of Δ E A B is
2 1 ( 3 ) ( 7 1 2 2 ) ( 5 4 ) = 3 5 7 2 2 ,
in exact agreement with Paola's solution.
Log in to reply
@Brian Charlesworth – See my solution using pure geometry.
Log in to reply
@Nihar Mahajan – Really nice solution, Nihar; well-deserving of an upvote. :)
@Brian Charlesworth – Thanks, I guess I had misread the discussion. I thought that Paola was saying that ABC wasn't a right angle.
Log in to reply
@Guiseppi Butel – Ah, o.k.. I guess that there is the making for another question, i.e., rather than having ∠ A B C be a right angle, make it some other angle, say 7 5 ∘ , and keep the rest of the question the same as Paola's. Then the solution would involve an extra couple of steps in order to find ∠ B A C .
@Guiseppi Butel – Hi Guiseppi. I just noticed your new question based on this one, and have one concern. If ∠ B is 9 0 ∘ then the area of Δ A B C is necessarily 6 . The question will work only if the condition that ∠ B is a right angle is removed; then it will be a great problem. :)
P.S.. I didn't want to formally dispute the question so I took this route, but I did notice that there was one dispute already, so I suspect that it raises the same issue as addressed here.
Log in to reply
@Brian Charlesworth – Thanks for the heads-up, Brian.
I have edited that parameter in the problem.
Log in to reply
@Guiseppi Butel – Great. I've now tried the problem and finally found the right answer after 3 attempts, (misread of what was being asked for on the first attempt, miscalculation on the second). I've written up an answer that relied heavily on a really useful but somewhat obscure formula, (there was already an answer posted so I chose to present an alternative approach). Thanks for posting the problem. :)
First we have to find the measurement of B D
Let A B = a , B C = b , A C = c , D C = x and B D = y
By angle bisector theorem
b a = x c − x ⇒ a x = b c − b x so x = a + b b c
Then by law of sines
sin 4 5 ° a + b b c = sin ∠ C y
y = sin 4 5 ° a + b b c × sin ∠ C
y = sin 4 5 ° a + b b c × c a
y = ( a + b ) sin 4 5 ° a b this is the bisector's length of in any rectangle triangle.
Second we have to find the area
Area of △ E A B = 2 1 a y sin ( 1 8 0 − A ) but sin ( 1 8 0 − A ) = sin A
Area of △ E A B = 2 1 ( a + b ) sin 4 5 ° a b sin ( A )
Area of △ E A B = 2 1 × ( 7 ) sin 4 5 ° 1 2 × 5 4
Area of △ E A B = 3 5 7 2 2 ≈ 2 . 9 1