Cool Pulley
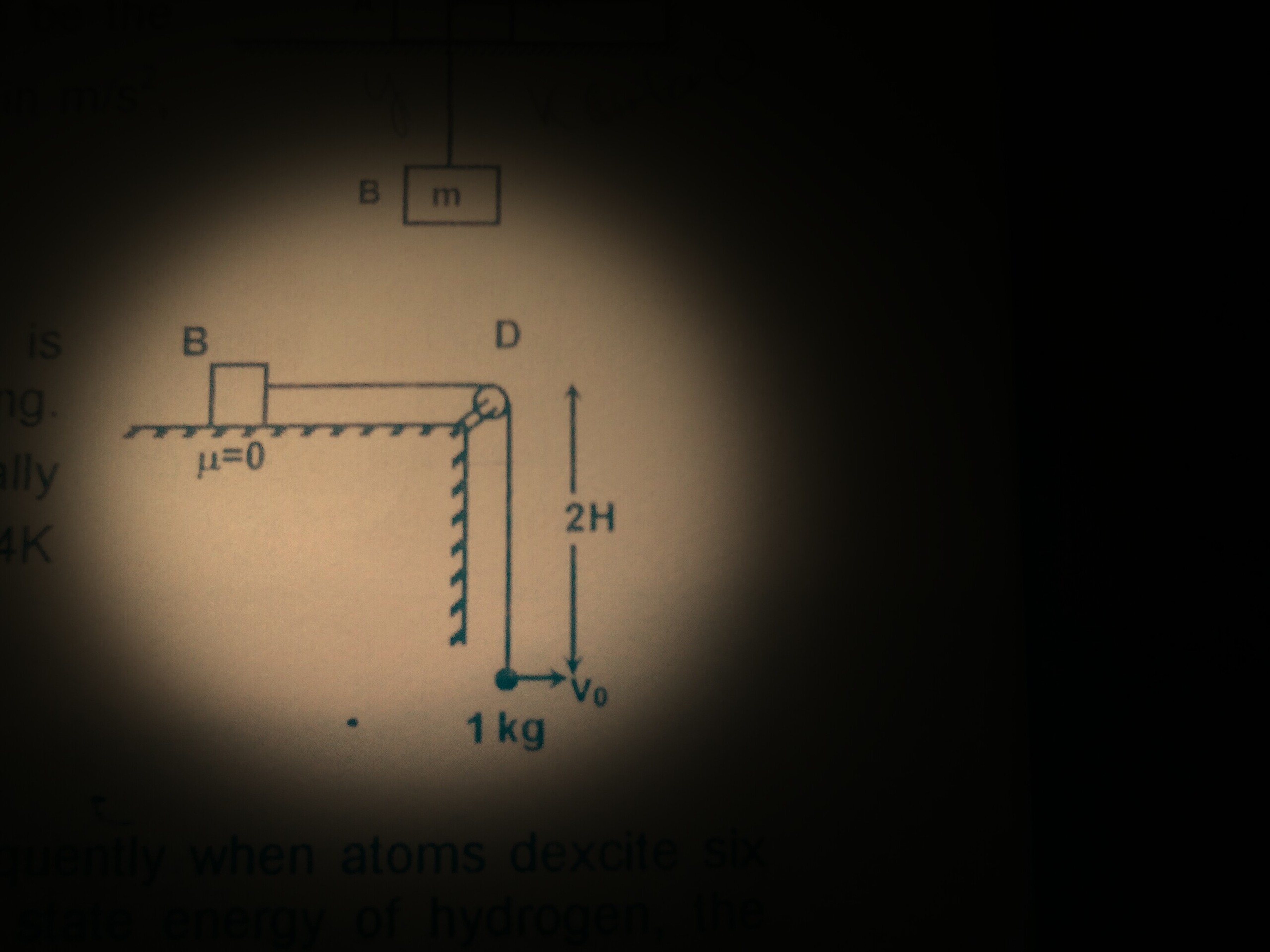 The figure above shows a block B of negligible mass connected to a particle of mass
1
kg
with a non-stretchable string. The hanging particle, at rest, is given a velocity
8
g
H
m/s
horizontally. The initial acceleration of block B is
K
m/s
2
. Find the value of
K
.
The figure above shows a block B of negligible mass connected to a particle of mass
1
kg
with a non-stretchable string. The hanging particle, at rest, is given a velocity
8
g
H
m/s
horizontally. The initial acceleration of block B is
K
m/s
2
. Find the value of
K
.
Details:
- Acceleration due to gravity g = 1 0 m/s 2 .
- H = 2 m .
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Can we use constraint relations?
Log in to reply
What do you mean?
Log in to reply
I mean that can i fix something like length of string in terms of given quantities and then differentiate or integrate to get the result?
Also, in your solution ; you have written
When the mass is first pushed out to the side, it is pulled down by gravity, but it also begins to swing, giving rise to a centripetal acceleration toward the vertical.
SIR, can you explain me why the mass begins to swing and rotate giving rise to centripetal acceleration?
Log in to reply
@Priyanshu Mishra – Initially the y component of velocity = 0 and x component of velocity is present . We know that a body moves in the direction of velocity and not the direction of force therefore the body initially moves only in x direction . At any instant the acceleration component which is perpendicular to velocity is the normal acceleration which is solely responsible for the necessary centripetal acceleration to change the direction of velocity . Hence the resultant of tension and weight (forces perpendicular to velocity) is the provide the normal acceleration = r a d i u s ( V t a n g e n t i a l ) 2 . At the given instant radius = 2H . This explains why it initially starts rotating .
But isn't the centripetal acceleration in the opposite direction of the gravitational acceleration?
Log in to reply
The force on the mass is upward, but the force on the block is in the opposite direction.
Log in to reply
What do you mean by this? Pls explain it asap.
Log in to reply
@Om Tiwari – I see that's a little hard to parse. What I mean is
- the centripetal acceleration points upward.
- but that means that the force that the rope feels from the hanging mass is downward.
- and then (following the direction of the force around the rope) the force on the block B is toward the right.
Let me know if that's still unclear.
Log in to reply
@Josh Silverman – Help with this https://brilliant.org/discussions/thread/vector-analysis/
The first thing to realize is that the block is massless, so it will have the same acceleration as the mass (since they're connected by the inextensible string).
When the mass is first pushed out to the side, it is pulled down by gravity, but it also begins to swing, giving rise to a centripetal acceleration toward the vertical.
Therefore, the total acceleration of the mass-string-block system is given by
a = g + v 2 / R = g + 2 H ( 8 g H ) 2 = g + 4 g = 5 g