Cornered baby circle
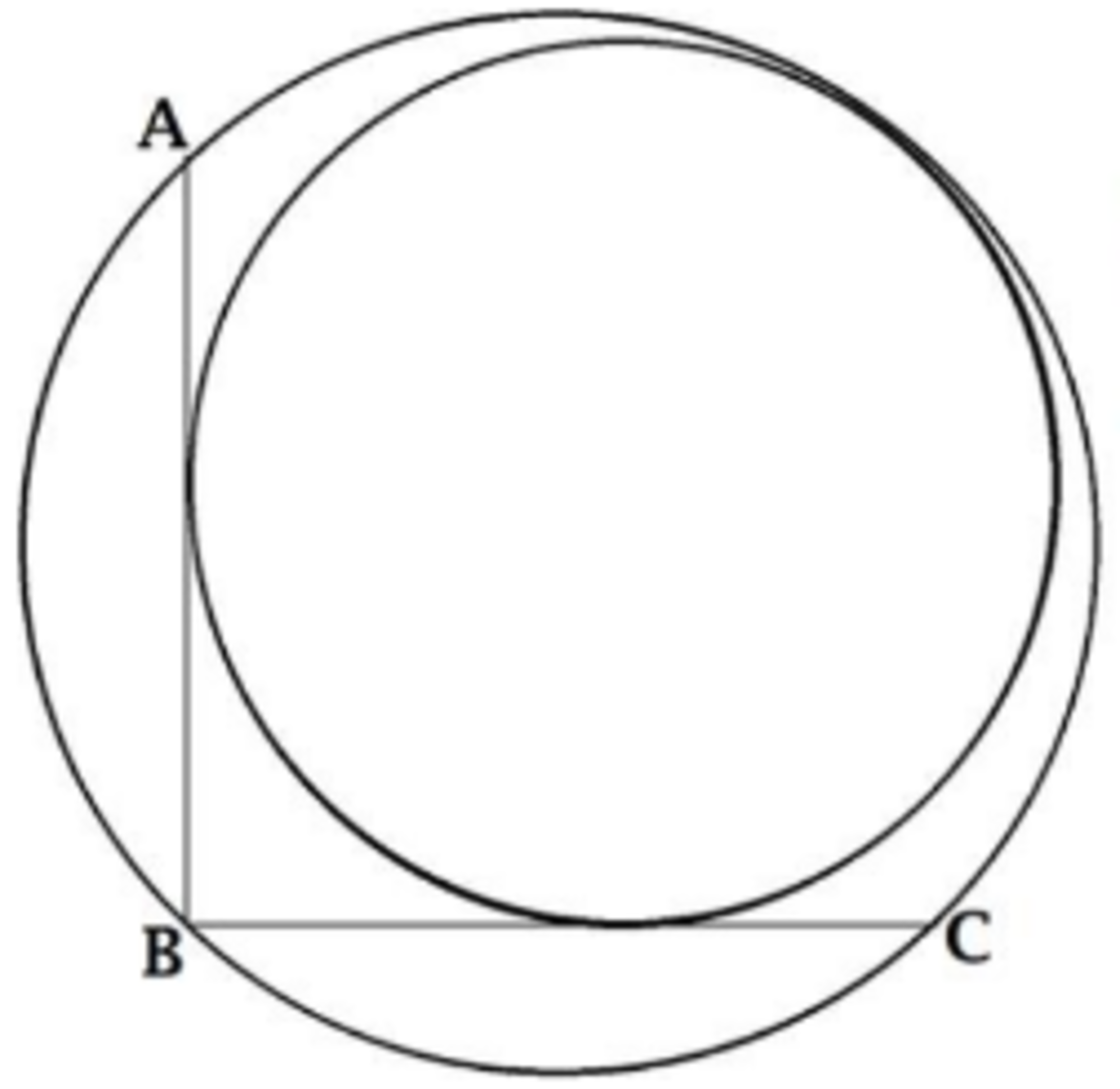
The above shows two circles internally tangent to each other at one point.
The smaller circle is inscribed inside the region between the 2 straight lines A B , B C and the larger circle. Also A B ⊥ B C and ∣ A B ∣ = ∣ B C ∣ .
If the radius of the larger circle is 5 2 , find the radius of the smaller circle to 3 decimal places.
The answer is 5.858.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
R * (rt 2 +1) /rt2 =10
R * (rt2 + 1) = 10rt2
R = 10 rt2 / ( rt2 + 1 )
Nice question. To make sure that the answer is unique, it should probably be mentioned that ∣ A B ∣ = ∣ A C ∣ and that A B ⊥ A C . Most people will make these assumptions but it may be better to be explicit.
Log in to reply
i think i mentioned that AB is perpendicular to BC....but they removed i think when they updated it .
Log in to reply
Ah, o.k.. They might have removed the condition that A B and A C are the same length as well, but that is still required for the answer to be unique.
Log in to reply
@Brian Charlesworth – I have updated it see now
Thanks for bringing this into our attention. We have accidentally edited the problem wrongly.
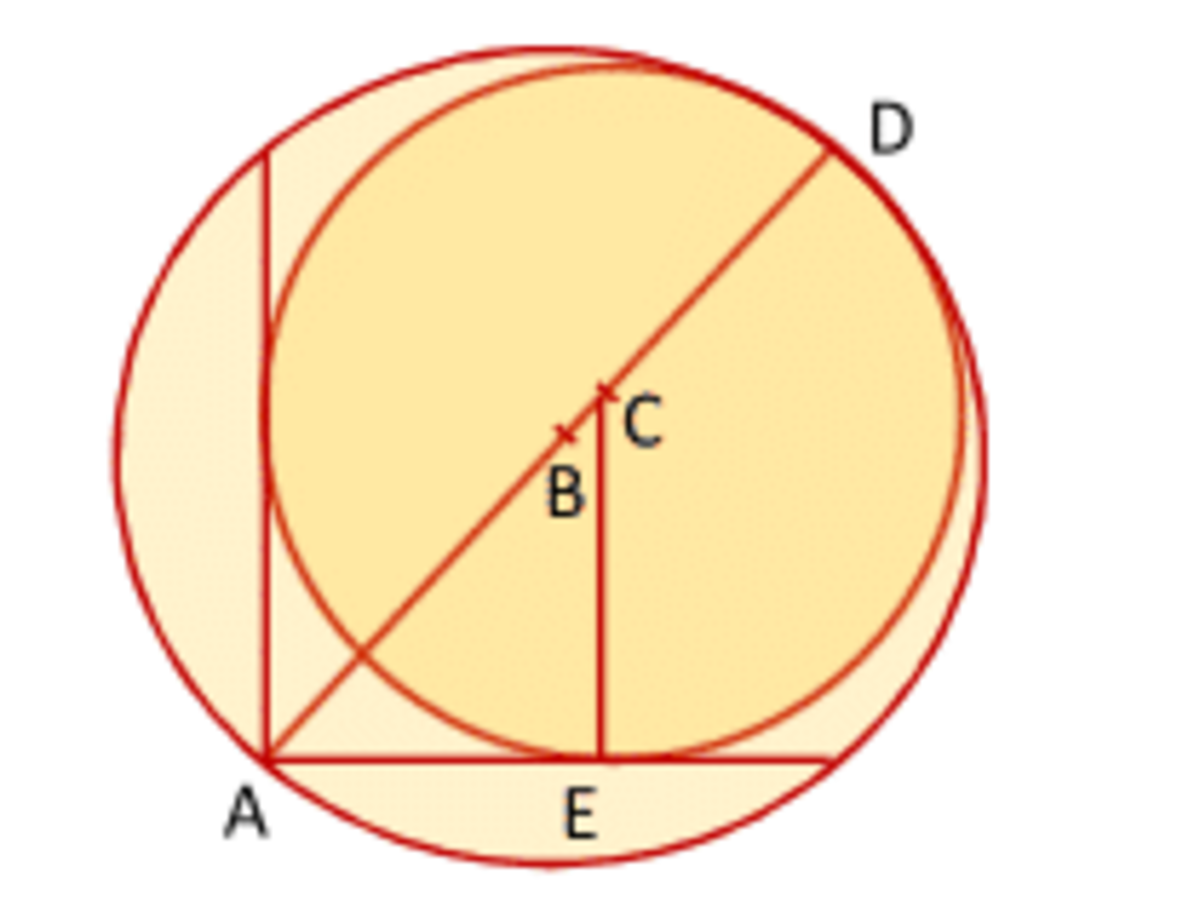
A B = B D = 5 2
D C = C E = R
A C = R 2
A D = 2 × A B = 2 × 5 2 = 1 0 2
A D = R × 2 + R
R ( 1 + 2 ) = 1 0 2
R = 1 + 2 1 0 2 ≈ 5 . 8 5 8