Coulomb's choreography
Exact solutions for many-body problems are rarely encountered in physics. The following problem deals with a non-trivial motion of four charges. Due to the symmetry of the problem it is possible to determine the trajectories of the charges analytically.
Four identical particles with mass and charge , orbit a charge as shown in the figure. The four positive charges always form a square of side while the negative charge stays at rest at the center of the square. The motion of the charges is periodic with period . That is, if the vectors , , describe the position of the charges then we have that It is also known that the side of the square oscillates between and . Determine the period T in seconds if the parameters and satisfy the relation
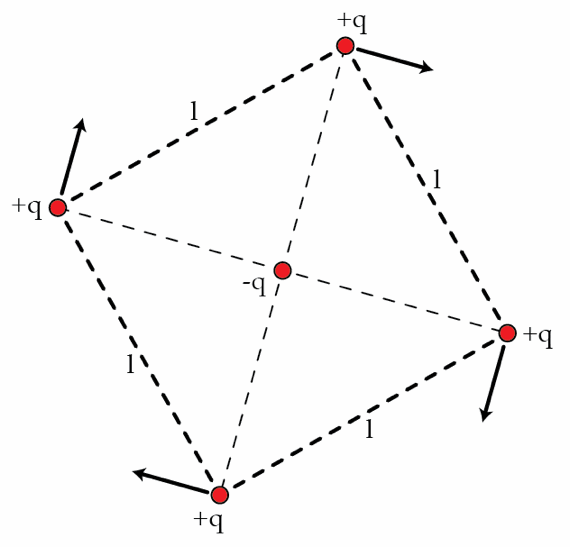
Details and assumptions
- Ignore any radiation from the charges.
The answer is 0.089.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We begin by noting that resulting force exerted on any of the charges is always directed toward the center center of square. Let l be the side of the square at a specific moment in time. Then the total force acting on a charge is given by F = F 1 + F 2 + F 3 + F 4 , as shown in the figure below.
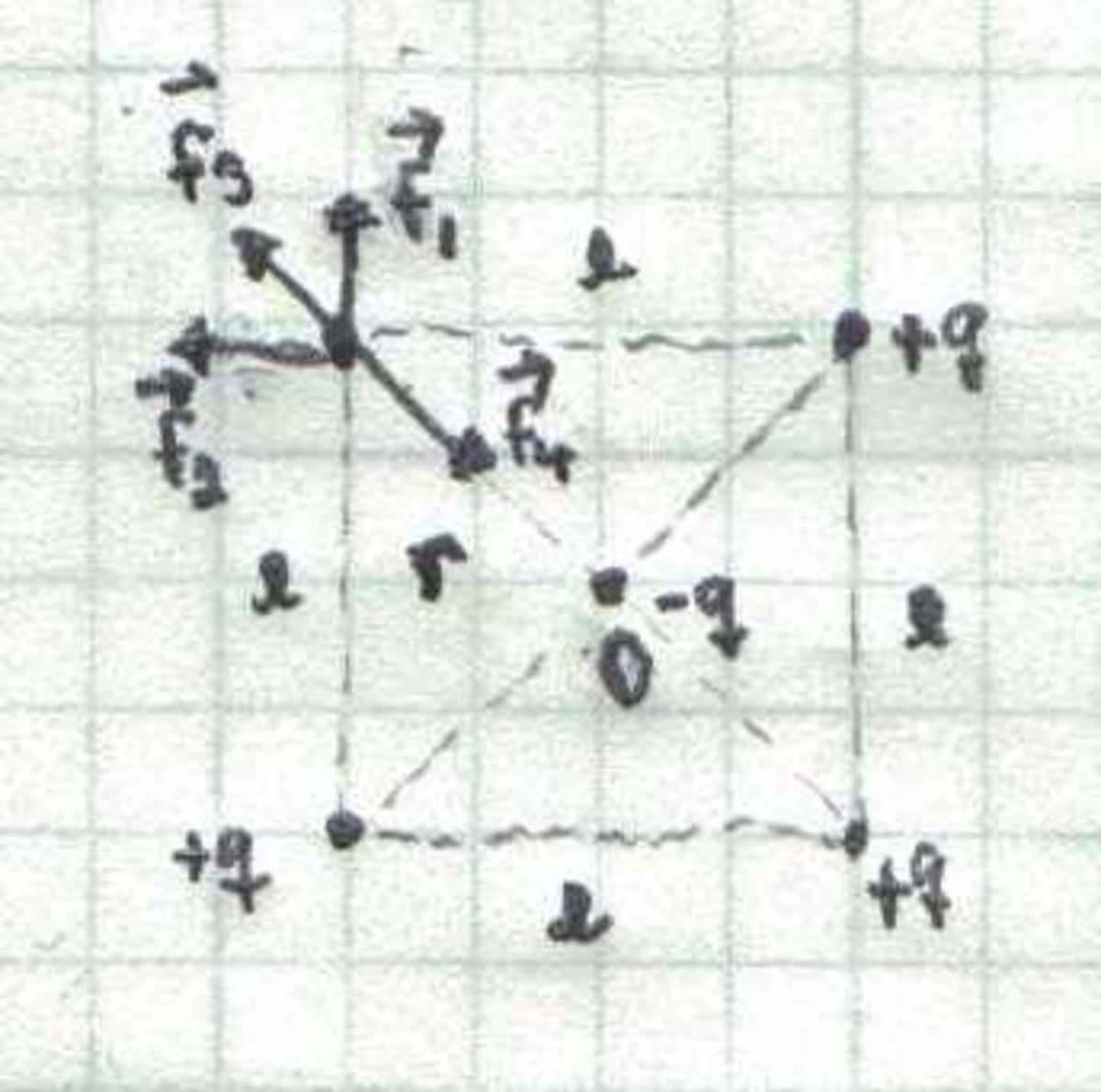
It is relatively simple to find its magnitude. Using some trigonometry we find that F = k l 2 q ( 2 ( 3 − 2 2 ) q ) = k r 2 q ( 4 ( 3 − 2 2 ) q ) where r = 2 l is the distance from the charge to the center of the square. This is a very important observation because it suggests that if we want to describe the motion of one charge, the rest of the charges can be replaced by an effective charge Q e f f = − 4 ( 3 − 2 2 ) q located at the center of the square. In addition, since both Coulomb and Gravitational forces are of the form F = γ / r 2 the orbit of any or the charges must be elliptical.
In the figure below, we show the positions of the charges corresponding to r m a x = 2 l m a x and r m i n = 2 l m i n .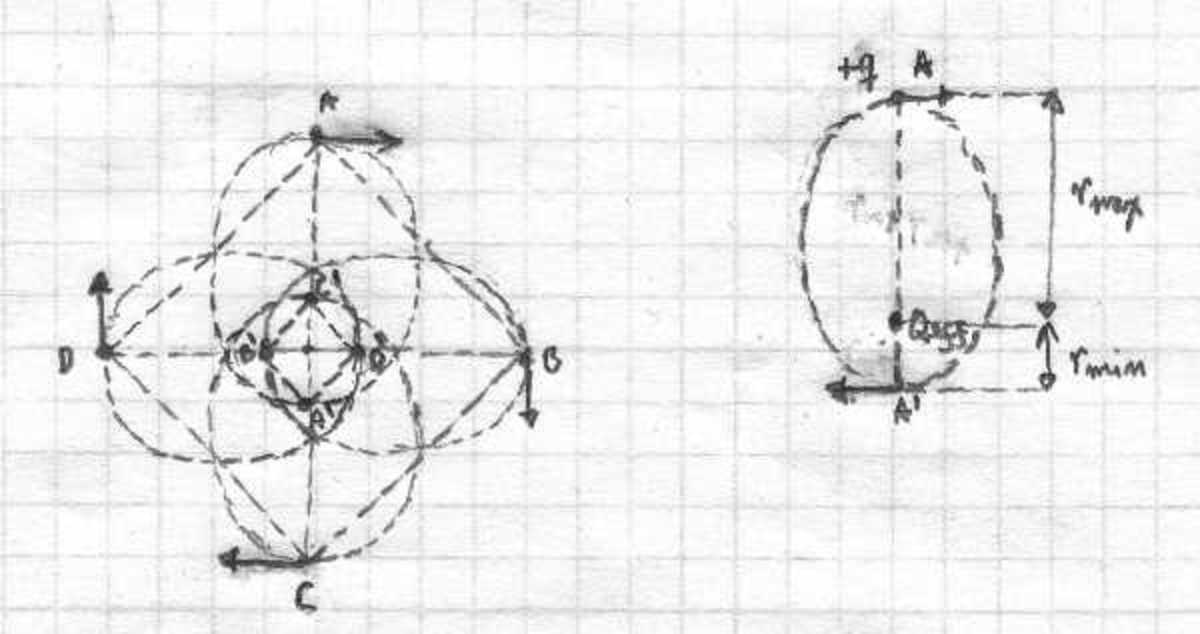
The semi-major axis of the ellipses is a = 2 r m i n + r m a x = 8 2 5 L 0 . Kepler's law states that the orbital period depends only on the semi-major axis. Consider a planet describing an elliptical orbit around the sun, then Kepler's law tells you that the period is given by T = 2 π G M s a 3 . Thus, by exploiting the similarity between Coulomb and Gravitational forces we can write T = 2 π k q ∣ Q e f f ∣ / m a 3 = 8 5 π 2 ( 3 − 2 2 ) k q 2 / m L 0 3 5 = 0 . 0 8 9 s .