Counting Squares!

In the 4 × 4 grid, how many squares have all 4 vertices on these dots?
Bonus : Generalize this for n × n grid.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I am wondering what your idea for a generalization is?
Log in to reply
For n x n grid , there will be (2n - 3) types of squares!
It will be sum of squares from 1 to (n - 1 ) + total sum of remaining (n - 2) types.
Log in to reply
There are much more than (2n-3) types of squares.
For larger n, there there n types of squares where they are parallel to the axis. Then there n-2 types of squares where one side is the vector (1, i ) for i = 1 to n-1.
Then there are n-4 types of squares where one side is the vector (2,i) for i=2 to n-2.
This continues on to
⌊
2
n
⌋
.
The harder part would then to be count all of these squares.
Note: The general answer is 1 2 n 2 ( n 2 − 1 ) . Can you prove it?
Log in to reply
@Calvin Lin – can anyone clarify my doubt if we do ( 2 4 ) ( 2 n ) we get the same formula it accidentally crossed my mind that for 2pt.s we have 1sq. Then dividing it by no. Of such squares to avoid repetition but now when I think deeply I feel some squares are repeated as there can be more than 1sq. From 2 pt.s
Log in to reply
@Chaitnya Shrivastava – Hey, I don't think this quite works. Perhaps you meant \frac{\choose{n^2}{2}}{\choose{4}{2}
@Calvin Lin – Can I ask? How about if we count the number of triangle (all kind of triangle), how many possible triangle could be formed? (Same question) -- (i got a challenge from my friends) Thx
Log in to reply
@Victor Zhang – Hey Victor, great question! Check out this question and this note .
@Calvin Lin – Is there a limit where this formula stars because with 2 and 3 it is obviously not working?
Log in to reply
@Susanna Weinberger – Can you elaborate on why it's obviously not working with 2 and 3?
With
n
=
2
,
1
2
n
2
(
n
2
−
1
)
=
1
2
4
×
3
=
1
, and there is only 1 square in that grid.
With
n
=
3
,
1
2
n
2
(
n
2
−
1
)
=
1
2
9
×
8
=
6
, and there are indeed 6 squares of 3 varying sizes in that grid.
@Calvin Lin – Please enlighten me with the proof!
Well , the right answer is given by Calvin Sir. I am trying to prove the given formula for n x n .
We know that T k = D k + S k
where
T k = Total number of squares we can make in a k × k grid,
S k = Total number of squares we can make using only vertical and horizontal lines in a k × k grid,
D k = Total number of squares we can make using only diagonal lines in a k × k grid.
Note that S k = 6 k ( 2 k − 1 ) ( k − 1 ) by the sum of consecutive integer square formula and D k = T k − 1 (This can be proven by induction on k). On a 3 × 3 grid there are 6 squares in total (i.e. T 3 = 6 ) so, T 4 = D 4 + S 4 = T 3 + 6 4 ( 2 ( 4 ) − 1 ) ( 4 − 1 ) = 6 + 1 4 = 2 0 .
By the way can anyone give an intuitive reason why D k = T k − 1 ? I find this surprising!
Log in to reply
There is a bijection that you can set up, to show that D k = T k − 1 . See this note .
Log in to reply
Thank you, that is a beautiful observation. I will take a look at what the picture is for the triangular and hexagonal versions of the question :)
I got 19. I missed the second case in type 5 image. So dissapointed.
can we do it by using combinations like by no. of ways of choosing 4 dots or 9 dots form 16
I draw all of the 45 degree straight lines and get a much smaller square that you didn't count in, which is half the size of the bottom left of the picture.It is a tilted square. Why it cannot count as a square?
How did you put pictures in your post? I found 13 MORE squares than the ones you show show in this example.. If you draw all 4 diagonal squares at the same time, the cross sections make squares too. This follows all of the rules in the question. It never says that the dots have to be the corners of the squares.. it only says that you have to draw straight lines between the dots. So the total is actually 33
Squares of 3 × 3 = 1 Squares of 2 × 2 = 4 Squares of 1 × 1 = 9
Then with each square of 2 × 2 we can form 1 a rotated square, in total 4 squares.
And with each square of 3 × 3 we can form 2 rotated squares.
⇒ we can form 1 + 4 + 9 + 4 + 2 = 2 0 squares.
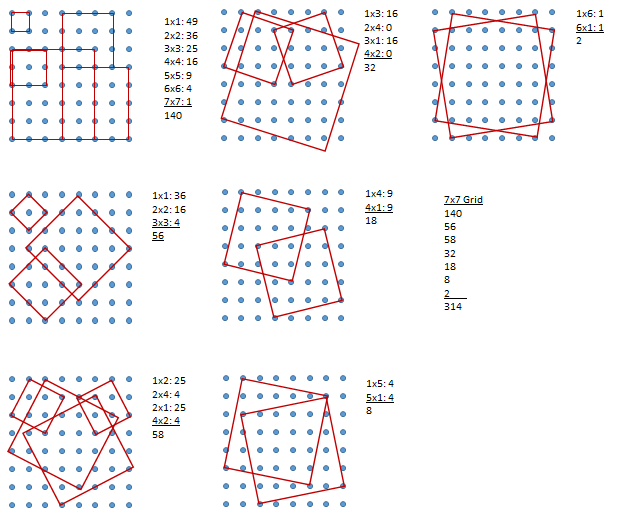
Unfortunately the generalized formulas presented don't work for larger values of n. The picture above shows a brute force counting of all squares in a 7x7 grid. The totals to the right of each grid show how many of each type (size) of square is represented as well as a sum of the total squares for that grid. Note that 1x3 represents a square who's side is one point to the left or right and 3 points up or down.
Calvin Lin's generalized solution predicts 196 squares. Hari prasad Varadarajan's generalized solution also predicts 196 squares. Manually counted we find 314 squares. I'll work on a generalized solution later.
I suppose that you have taken in account a 8×8 square and used the formulas for a 7×7 one, thus you are getting 196. If the formulas are used for 8×8 squares they both will give the answer as 336. So, you need to find 22 more squares manually.
(Note in the given pictures that the square is a 8×8 one and because of this you have taken 49 1×1 squares.This was where I caught you because had it been a 7×7 one then there would have been 36 1×1 squares.)
Your 7x7 grid contains 8x8 dots. If you add the squares 2×3:9, 3×2:9, 2×5:1, 3×4:1,4×3:1 and 5x2:1 you find the missing 22, making 314+22=336 or n^2 (n^2-1)/12 for n=8. n=7 gives 196.
I found a pattern and have generalized a formula. The number of squares which can be formed from a n x n dot grid is, (n-1)^2 + 2 [(n-2)^2] + 3 [(n-3)^2] + 4 [(n-4)^2] ................ Do this till one of the term becomes zero (i.e) n terms. For eg. For a 3 x 3 dot grid the number of squares formed is 2^2 + 2 [1^2] + 3*0 =4+2 =6
Can you explain how you arrived at the formula? This is the generalization that is hinted at.
I too want to know how do you get that
This could also have been done by a simple formula n(n+1)(n+2)/6 ie 4 5 6/6 = 20
Hi could you please clarify, this formula does not work for any other n. ie 3(3+1)(3+2)/6 = 10 not 6
No. of squares of type 1 in the image = 1
No. of squares of type 2 in the image = 4
No. of squares of type 3 in the image = 9
No. of squares of type 4 in the image = 4
No. of squares of type 5 in the image = 2
So , Total No. of squares = 1 + 4 + 9 + 4 + 2 = 20 squares that can be drawn on a 4x 4 grid. :)