Counting triangles
How many triangles of any size are there in the figure above?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Moderator note:
A mathematically full solution needs to not only demonstrate the answer (as shown via the GIF) but show the maximum can indeed go no farther.
In this case an argument can a.) first note any triangle will need to be equilateral and then b.) use constraints on size.
How did you make the GIF?! It's amazing!!
Log in to reply
Thanks. I simply made 20 images from the diagram in the problem, and uploaded them to https://giphy.com/create/slideshow
There's more than 20
Log in to reply
Oops no that's correct. Lol
there are only 20 triangles, look at my solution below.... ...
So is there a mathematical theorem that can be used to identify the number of triangles? And based on the Challenge Master's note related to equilateral, the original question does not require equilateral triangle counts, and while I can see it's not possible to create a triangle that isn't, is there a proof for that as well?
Log in to reply
Note that any triangle is equilateral.
This can be a quick observation as all the possible lengths triangles are integer multiples of smallest segment that you can see here. Also note that the smallest triangles are equilateral, so at any point you should have at least one angle of 6 0 ∘ , which will ensure that all possible sizes of triangles must have all angles equal to 6 0 ∘ , making the point in concern True .
Use constraints on size.
It is concerned with the size for each triangle. Note that the smallest line segment that you can make between two successive points is the side length of smallest triangle you can see. Since you can see from the figure that there can only be a maximum of 3 of these segments lined up one after the other to create the side of the largest possible triangle, conclude that you cannot find any bigger triangles of side length greater than 3 of the lengths of smallest segments. Now the easiest way one can proceed is by just simply counting the number of triangles of side lengths of 1, 2 and 3 times the factor of the smallest segment.
I don't know about a mathematical theorem, but there is proof that equilateral triangles aren't necessary, which then subsequently changes the constraints on size to have a different definition.
20 is incorrect. I count 36.
Log in to reply
Feel free to create a detailed report with your working.
@Challenge Master - Why is there a requirement for the triangles to be equilateral?
Other formations like this can be created from 12 triangles that are not equilateral - As long at the 6 inner triangles are made from 3 e d g e s that intersect each other at a single vertex, with each subsequent outside e d g e extended until they form the 6 outer triangles, then there are also 20 triangles in total.

However, I'm sure there are also constraints on the lengths of the inner e d g e s , but the point being that equilateral triangles don't seem to be necessary.
Log in to reply
In the case of this example, all of the possible angles are multiples of 6 0 ∘ . The only triangle that satisfies this is the equilateral triangle.
Please update your solution to reflect the points in the note. Thanks!
Log in to reply
I've been trying to reconcile what you said relative to what I illustrated, but I'm failing.
I have to assume that you're talking about the example in the problem when you say "In the case of this example". However, the problem doesn't state that they are equilateral, nor does it state the length of each edge. The triangles being equilateral is being assumed from an observational perspective. There is the possibility that the angles in the figure in the problem may not be perfectly 6 0 ∘ , and only perceived to be. But, as I've illustrated, it's ok for them not to be.
Even if they were equilateral, the fact that they exist doesn't necessitate them as a requirement. I maintain my assertion that there is a broader and more significant argument (albeit more complex than I've been able to describe) - which encompasses equilateral triangles - to result in 20 identifiable triangles from a figure of 12 triangles arranged in this manner.
The constraints on size then becomes the number of vertices that exist on each edge.
In response to Challenge Master's note:
(Reply to Josh Oshman's comment)
Note that any triangle is equilateral.
This can be a quick observation as all the possible lengths triangles are integer multiples of smallest segment that you can see here. Also note that the smallest triangles are equilateral, so at any point you should have at least one angle of 6 0 ∘ , which will ensure that all possible sizes of triangles must have all angles equal to 6 0 ∘ , making the point in concern True .
Use constraints on size.
It is concerned with the size for each triangle. Note that the smallest line segment that you can make between two successive points is the side length of smallest triangle you can see. Since you can see from the figure that there can only be a maximum of 3 of these segments lined up one after the other to create the side of the largest possible triangle, conclude that you cannot find any bigger triangles of side length greater than 3 of the lengths of smallest segments. Now the easiest way one can proceed is by just simply counting the number of triangles of side lengths of 1, 2 and 3 times the factor of the smallest segment.
How can you say you didn't miss any triangle by mistake? @Marvin Kalngan
There are 36 triangles in the image.
How can I be sure that I am not missing any triangle?
There are 36, Triangles are made from sections: -5,9,10,11; etc.
Log in to reply
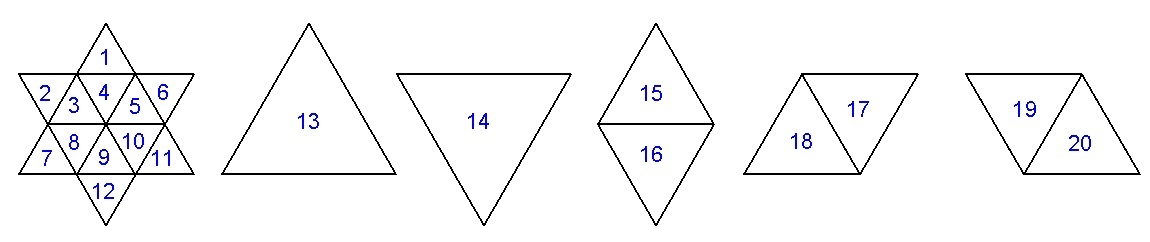
Marvin's solution accounts for groups of triangles, as do all of the other solutions that count 20.
Triangle 13 to triangle 20 in his solution represent the groups.
- 13 = 1,3,4,5,7,8,9,10,11
- 14 = 2,3,4,5,6,8,9,10,12
- 15 = 1,3,4,5
- 16 = 8,9,10,12
- 17 = 4,5,6,10
- 18 = 3,7,8,9
- 19 = 2,3,4,8
- 20 = 5,9,10,11
A number of people are claiming more than 20 triangles, but are not showing their working. Could you kindly show yours please, Elizabeth?
It would be handy if you could list triangle 21 to 36 in the same format I have done, using Marvin's 12 numbered triangles.
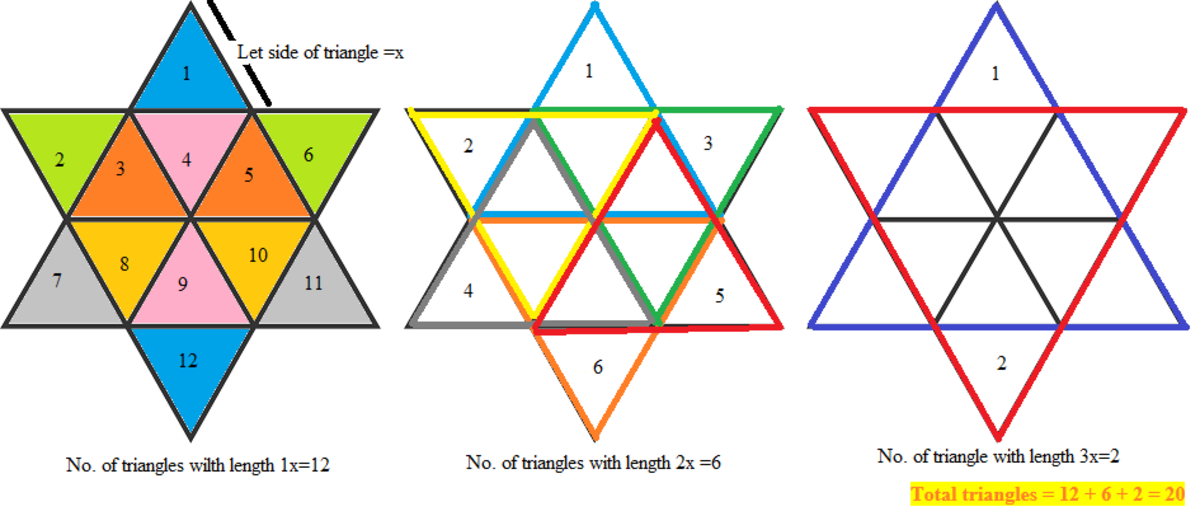
We will do this problem using casework.
Triangles with Area 1: 12 Triangles
Triangles with Area 4: 6 triangles.
Triangles with Area 9: 2 Triangles.
12 + 6 + 2 = 20 Triangles.
I count 24, Triangles with Area 9: 6 Triangles [email protected]
Log in to reply
Can you show us where the other 4 triangles came from?
Log in to reply
I think Mark may be counting the different rotations. At least doing that results in 6 and fits with his answers.
Log in to reply
@John Oshman – That was my assumption too, but then if it was true that he was counting rotations, his answer should be 60.
( 1 2 × 3 ) + ( 6 × 3 ) + ( 2 × 3 ) = 6 0
Whatever be the answer but I felt the logic is AWESOME!!!
Triangles with area 1: 12. Triangles with are 4:18. Triangles with area 9:6. Total is 36 triangles.
Firstly, by counting one triangle = 12
Secondly, by counting with 4 triangles to one = 6
Thirdly, by counting with 9 triangles to one = 2
Thus, Total triangle possible => 12+6+2=20
I can find thirty triangles.
Log in to reply
Which are the 10 triangles, that Venkatachalam J does not list? You must have counted some identical ones twice or more.
Is there a general solution or method for these type of problems?
Yes, but not easily. It's actually easier to just count all the triangles, especially if the figure is "small enough."
Count upward or downward direction and multiply by 2
[Edit May 31, 2017] While I could update my solution to be in line with the Challenge Master note, I feel it would be an injustice to the other solutions that have already provided this work. By all means, feel free to like the GIF, but I encourage upvoting other solutions that offer what the Challenge Master is looking for.