Cover a rectangle
Any non-square rectangle can be covered by two similar, but slightly smaller rectangles.
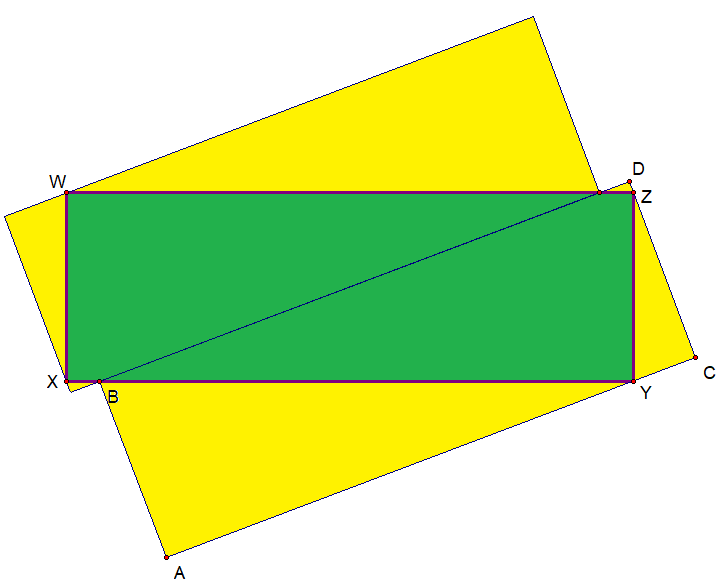
In the picture, rectangle W X Y Z which has aspect ratio W X X Y is covered by two slightly smaller rectangles. These two smaller rectangles are the same size, W X A B = k < 1 and k is as small as possible.
For what aspect ratio is k only one one-millionth less than 1?
The answer is 18.8296.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Okay, 18.8296 checks out
Log in to reply
I don't think so. I double checked, but I'll try drawing it now just to be sure.
Edit: I can't quite draw it with a=18.8296, k=.999999 because sketchpad doesn't go to that many digits of accuracy. But a=9.4148 gives k=.99998
I got the same answer as Jeremy. I used a similar method (except using trigonometric ratios instead of similar triangles) and came up with the same k equation, and used a TI-84 graphing calculator to find the intersection of y = k and y = 0.999999 which also gave me 18.8296.
I don't understand this part "Call A B = k so A C = a k ." In the problem, you define k = W X A B , so after you set Z Y = 1 , W X = 1 , and A B = k anyway. And why is A C equal to a k ?
Log in to reply
k is the scale factor from the green to the yellow rectangle. a is the aspect ratio comparing sides of any of the rectangles.
AB/WX=k, AC/AB=a, so multiply to get AC/WX=ak. Since WX=1, AC=ak
Log in to reply
Are you saying that the green rectangle and yellow rectangle are similar, i.e. they have the same aspect ratio? It does not say that in the problem.
Log in to reply
@Jon Haussmann – Does the first sentence not make it clear?
Let Z Y = 1 so the aspect ratio is W Z = a . Call A B = k so A C = a k and call B Y = y so B X = a − y .
By similar triangles Y C = y k and D Z = y k ( a − y ) = y a k − k . Subtracting gives C Z = 2 k − y a k
Similar triangles again gives A Y = 2 k y − a k = k ( 2 y − a ) .
Since A Y + Y C = A C we have 2 k y − a k + y k = a k or, since k = 0 simplify to 2 y 2 − 2 a y + 1 = 0
The positive solution to this quadratic is y = 2 a + a 2 − 2 . This means A Y can be written as k a 2 − 2 .
Now the Pythagorean theorem on △ B A Y gives k 2 + [ k a 2 − 2 ] 2 = y 2 .
Solve to get k = a 2 − 1 y
A final substitution of k for y gives a formula for k in terms of the aspect ratio:
k = 2 a 2 − 1 a + a 2 − 2
I decided to let Wolfram|Alpha solve for k = 1 − 1 0 0 0 0 0 0 1 and it gave me an interesting exact form which is approimately a = 1 8 . 8 2 9 6