Covering a circle
Circles have the strange property that if you increase the size of any circle by even the tiniest amount , you need at least three circles of the original size in order to completely cover the new, slightly larger circle.
Are there any other shapes that share this property?
The 3 overlapping orange circles have the same radius as the black circle. It takes 3 of these circles to cover the slightly larger dashed circle.
Note 1 : For other shapes, rather than increasing their radius, which is generally only associated with circles, you are scaling up their shape proportionally.
Note 2: You can rotate the shapes any way you like.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
So I'm guessing that all regular polygons share this property.
Log in to reply
Maybe the better question to ask is, "what shape doesn't have this property"?
Log in to reply
Well, I would guess that any non equilateral triangle can be covered by two smaller similar triangles.
Log in to reply
@Geoff Pilling – True. This will require some investigating. It is pretty easy to see for a right triangle.
And another question... Are there any shapes that take more than 3?
Log in to reply
@Geoff Pilling – A shape with a lot of 'arms' would take more than 3. For example, a 5 pointed star would take 5.
Log in to reply
@Jeremy Galvagni – Oh, probably. But I'm going to have a closer look at your suggestion of rectangles with those proportions.
@Jeremy Galvagni – Hmm.... Are you sure? I'll need to think about that one for a bit...
@Jeremy Galvagni – Actually it isn't clear to me that 5 would be enough for a five pointed star. For instance, in the limit, where your star- shaped region has area zero it could take twice as many as the number of points. For example, if your original shape was the union of 5 line segments that all share a common endpoint and have an angle of 7 2 ∘ between consecutive spokes, then wouldn't it require two of the original figure per spoke ?
EDITED: Nevermind. If it were really zero area, you would only need one figure per spoke and an additional one for the center. Still, more than the number of spokes.
@Jeremy Galvagni – OK, after thinking about it some more, I believe that if you allow non-convex shapes, you can probably cause it to require many copies. Think about an annulus which is very thin compared to its radius. It is like asking how many semicircular arcs with radius 1 (just the curve, no area) it would take to cover a semicircular arc with radius 1 + ϵ . As a matter of fact I don't see how to do it with finitely many. Now I realize that going from "shape" to curve is a stretch, but this curve is the limit of thinner and thinner half-annuli, so it should be possible to get an arbitrarily large "covering number" (if I may call it that) by considering thinner and thinner annuli.
Now if we restrict our attention to convex shapes...
The question is whether there are any other shapes where it can be done with 3. Can you cover the shape of a slightly larger square with 3 squares?
If you think if a rectangular, you might be able to cover the bigger one with 2 original ones
Log in to reply
I don't think so, Linus. I can't see a way to do it.
hmm.. let me try in a different way
Log in to reply
Yeah, it's obvious that it can be done as Jeremy has suggested. So, now the problem has become even more interesting.
It would be interesting to somehow classify which shapes do, and do not, satisfy the criteria. There appear to be many more shapes than I expected when I first wrote up the problem... :-/
Log in to reply
I'm still not 100% sure what we are looking for. We seem to have competing ideas:
- For a given shape A , determine the minimum number n of congruent shapes that required to cover it, if no single shape is allowed to completely cover A .
2a. For a given shape A , determine the minimum number n of smaller similar shapes that required to cover it.
2b. What is the minimum size for the similar shapes?
Your original question seems to be asking whether there are other shapes for this second part where n ≤ 3
Log in to reply
Good point!
The question isn't asking about 2b, only considering shapes that are just slightly smaller than the original.
I believe that 1 and 2a are likely similar (no pun intended! :) )
Yes. It definitely seems somehow that symmetry is the key!
Log in to reply
It seems like the key is that the shape has to have both rotation and reflection symmetry... All regular polygons share this property, and so do circles.
Log in to reply
Yes, I believe this is definitely on the right track! I wonder... Does anything else fit the bill besides regular polygons and circles?
Log in to reply
@Geoff Pilling – A lot of non-convex figures would require three or more, so it's easier if we first investigated just convex figures. Is there anything that isn't a regular polyhedron, or a circle? Hmm... there might be.
Log in to reply
@Michael Mendrin – Yeah, didn't you mention that some rectangles required 3?
Log in to reply
@Geoff Pilling – I mentioned that, but obviously it's not true of all of them. Maybe none.
Log in to reply
@Michael Mendrin – I think just squares require 3.
Log in to reply
@Jeremy Galvagni – What about regular hexagons, like how I trying to do it with just 2?
Log in to reply
@Michael Mendrin – I mean among rectangles, only squares require 3. I haven't given other regular polygons much thought.
Log in to reply
@Jeremy Galvagni – ...okay, right. You've probably already worked that out. Meanwhile, I'm looking at other figures. Too much to do.
@Michael Mendrin – If you allow non-convex figures, you can concoct figures that take arbitrarily many. In fact if you allow figures with no area (curves) then I think a semi-circular arc of radius 1+\epsilon cannot be covered by finitely many (or even countably many?) semi-circular arcs of radius 1.
I though I had posted a comment along these lines already, but I can't seem to find it.
Log in to reply
@Varsha Dani – Well, that's a good point...any arc of one radius cannot even be in part covered by another of a different radius, except at two points at most.
can triangle be?
Yes, an equilateral triangle.
Since there is no way to cover more than two corners with one triangle (that is smaller than the original), you need at least three equilateral triangles to cover it.

Judging from yours and Michael's examples it would appear that all regular polygons share this property. It would be interesting to examine which triangles and rectangles do n o t share the property....
Log in to reply
Interesting.... Is it true for a regular pentagon?
And I suspect that the only triangle for which it's true is an equilateral one but I can't say for sure... 🤔
Log in to reply
I think every regular polygon exhibits this property since it can be divided into many isosceles triangles (which do have this property) whose common vertex will be the center of the polygon.
Log in to reply
@Abha Vishwakarma – I'm not so sure that isosceles triangles have this property, do they?
Log in to reply
@Geoff Pilling – Please see my solution and tell me if I misinterpreted your question.
...right, what shape doens't have this property?
What is the property you are referring to? Are we covering with (some number 3? of) circles of a certain size? 3 congruent polygons? Some other number of congruent polygons (n n-gons)?
Log in to reply
Jeremy, the more interesting question is, is there any simple closed figure that can be covered by two identical versions of it that are a bit smaller? So far, with the figures we've examined, it requires three.
Geoff's problem asks if any other figure shares this property with the circle, and the answer is, yes, there is at least the equilateral triangle as an example. But hardly the only one. It seems like all other simple closed figures share this property. Can you find any that does not share this property?
Log in to reply
I haven't been asked to help vet problems. I would have reported this or asked for clarification.
As for your question: try a rectangle.
Log in to reply
@Jeremy Galvagni – I think there's been more changes in Brilliant, about that, Jeremy.
I can try a rectangle, but I don't think a rectange can be covered with two slightly smaller versions of it.
Log in to reply
@Michael Mendrin – A rectangle of aspect ratio between 1/2 and 1 (exclusive) can be covered by two slightly smaller similar rectangles. The aspect ratio sqrt(2)/2 allows the two rectangles to be smaller by that same factor.
Log in to reply
@Jeremy Galvagni – Is that right? That's interesting, that should be noted here in solutions.
@Jeremy Galvagni – Are problems on here vetted? It would make sense, of course, but it seems to me that the 4 problems I posted just appeared on the site and people started solving them.
Sorry for the question, but I'm new, having discovered the site less than a month ago
Log in to reply
@Varsha Dani – Varsha....Community problems is basically a free-for-all. Only when they become POTW they are (hopefully) thoroughly vetted. Lots of problems posted here have.....uh.. problems with them.
Log in to reply
@Michael Mendrin – Looks like our responses crossed... ;-)
@Michael Mendrin – Ah, makes sense.
So who does the vetting? Are people approached specifically? Since Jeremy mentioned not being asked to vet the problem, I suppose it is not only admins.
Log in to reply
@Varsha Dani – Well, anyone can lodge a complaint through "View Reports", so that once there's more than one report, Brilliant Staff gets involved when they are able to get around to it. But problems and complaints come in faster than they can review, and so after a while, troubled problems just get lost in history. I'm not even sure if they're still maintaining a volunteer staff of Moderators for that any more.
Log in to reply
@Michael Mendrin – Lately, the only reports I've made that have been resolved by staff are when a staff member, (usually Calvin), has been notified directly, (a practice I don't condone as Calvin is busy enough, I'm sure). It's got to the point where once I have the attention of the author of the disputed problem we figure out a way to deal with the issue without staff, or I suggest that the problem be deleted are reposted with the necessary corrections made. We're both moderators, but neither of us (I assume) has the power to resolve reports or change posted solutions, as that requires staff to correct points awarded, etc..
Log in to reply
@Brian Charlesworth – Sometimes the author willingly works with those that have reported something, others just don't respond or refuse to do anything about it. Sometimes the Staff intervenes, sometimes they don't. A lot of bad problems just float by. Fortunately, the majority of them are all right, though.
Log in to reply
@Michael Mendrin – Given the volume of submitted problems, there are a remarkable number of good ones. Another issue is duplicate problems.
@Varsha Dani – Yes. Problems are vetted quite often.
Since Brilliant can't vet all problems in excruciating detail, it especially vets the ones that it plans to promote. Making sure the picture is clear, the explanation is descriptive, and the answers are correct, etc.
@Varsha Dani – I was asked to take a look at the upcoming featured problems of the week every Friday or Saturday for a few months, but not for the last two weeks.
I believe all triangles that aren't equilateral can be covered with only two slightly smaller versions of themselves.
Log in to reply
@Geoff Pilling – Okay, what about a right isoceles triangle? How would 2 of them cover one slightly larger?
Log in to reply
@Michael Mendrin – Well, how about if you use one to cover everything except for one of the smaller sides. Then you cover up that side with the hypotenuse of a second triangle?
This problem is worded horribly. You need to explain what you are doing much better. Maybe color code each circle...?
Log in to reply
Thanks for your input... Although, is "horribly" perhaps a bit harsh? :-/ Any suggestions on how the wording could be improved, besides color coding?
No doubt you're considering posting a similar problem for 3 dimensions. :) I suspect one would require 4 spheres of radius r to "cover" a sphere of radius r + d r . As for cubes, tetrahedrons, etc., .... ugh.
Log in to reply
Hahaha... That would be cool! But describing the "covering" part? Hmmmmmmmmmmmmm... Can we conclude yet, that for convex (2D) shapes, that it is only true for circles and regular polygons?
Log in to reply
The 3D one is interesting... For a sphere, is it, uh.... 4?
Log in to reply
@Geoff Pilling – I would guess it would be 4, yes.
Edit: Definitely 4 will do. No doubt about it. And it cannot be done with 3.
Log in to reply
@Michael Mendrin – It seems it would be four for a tetrahedron too...
@Geoff Pilling – Well it would certainly be at least 4. I'm not sure if I'm convinced 4 is enough...
Log in to reply
@Varsha Dani – Hahaha.. My thoughts exactly... Its much harder to test out than it was in 2 dimensions...
A rectangle of aspect ratio between 0 . 5 and 1 can be covered by only two similar rectangles rotated 90 degrees. When this ratio is 0 . 5 the smaller rectangles can be shrunk by the same ratio.
It turns out the rectangles can be even thinner.
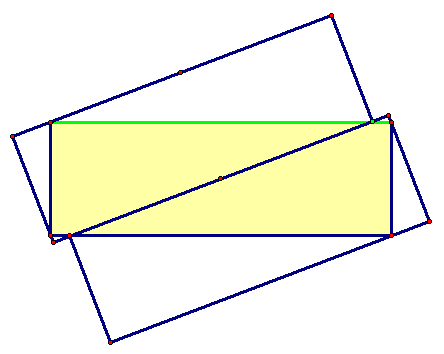
Here the aspect ratio is 1/3. All three rectangles are the same size in the picture but there is room to make the covering rectangles slightly smaller. The green dot is not touching the green line but is a tiny bit above it.
Ah, very clerver, @Jeremy Galvagni !
So, I wonder... Can we show that a rectangle can't be covered by 2 slightly smaller ones if the aspect ratio is less than 0.5?
Log in to reply
Yes, I added a picture.
Log in to reply
Interesting... So I wonder if, in fact, all rectangles can be covered with 2 smaller ones... :-/
There we go, it's the exception. Well done :)
Thank you jeremy, thats very cool of you
Do you mean any polygon will share the same property?
Given that a circle has this property, obviously an annulus does as well.
However, there is a problem with the way the problem is worded. It talks of increasing the radius slightly. What is the radius of a rectangle, or of a triangle?
Good point... I've added a clarification at the bottom. Do you think it makes sense?
Log in to reply
Hmm. I suppose what you reallly mean is scaling it up proportionally, and so this or a simliar (pardon the pun) wording would be clearest.
I guess the information given above isn't complete. I mean, the property given for the cercle is not clear: do we have to pay attention to the number of cercles required to fill the area of the new cercle, or do we have to pay attention to the fact that the area of the new cercle can be filled by an exact number of cercles with the same radius?
I tried to solve the problem imagining all the other posible shapes, for example, the square: you just need two identical squares to fill the area of a square with the same perimeter. It tells me that the number of the shapes is not relevant: while in the case of cercle we needed three other identical cercles, with the square we only need two.
I thought, after all, that the answer for the question made above is to complete the area of a shape with a determinate number of identical shapes.
What do you think?
Are you sure we can cover a square with only two slightly smaller squares? @Michael Mendrin argues above that we can't.
The problem is to cover a square larger than an unit square using two unit squares. Can you do that?
Yes because there are only 2 answers so its a 50/50 chance and also because it sounded like the right answer
Is this a correct interpretation of your question? I think I have missed something so I had to post this. I found how isosceles triangles follow this property.
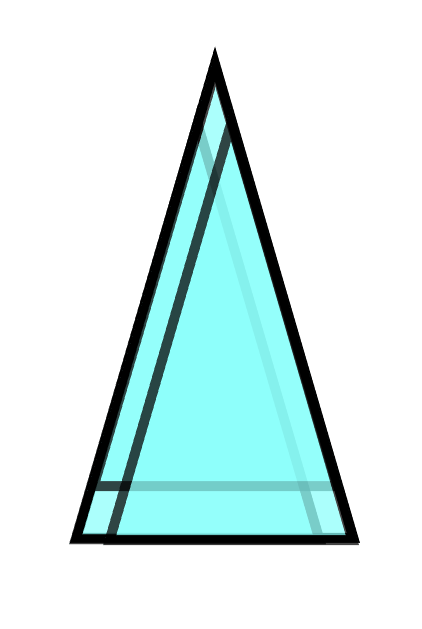
This is an image of three small isosceles triangles covering the area of the larger triangle (which has the same angles as the smaller one and is just a little larger).
I understood your question as "You need at least three original figures to cover the area of the little larger figure." Am I right? And if I am then I think every triangle should follow this property since the angles won't change.
In your example if you rotate one of them 90° and place it over the short side of the original, I think you can cover it with two triangles.
Log in to reply
Ahh... That's true. So the important condition was that there should be at least 3 smaller figures. But then there's this question in my mind - A circle is a regular polygon with infinitesimally small sides, so we could imagine an infinite amount of isosceles triangles with a common vertex as the center of the circle, and since an isosceles triangle needs just two smaller ones to cover its area, the circle should also need only two smaller ones, but it needs three. How can this be explained?
Log in to reply
Interesting solution, but unfortunately you're not allowed to cut up the circles... 🤔
I think ovals work for this problem, correct me if I am wrong
I think ovals probably fit into the same category as non-square rectangles in that they don't work, but I could be mistaken...
Imagine a regular polygon with infinite sides....
You mean a circle?
Simple answer - Any regular polygon.
That's my gut instinct... (Including a circle as a regular polygon with "infinite" sides) But can we prove it?
Also, what about rectangles, as @Michael Mendrin has been discussing?
It works with square beside all side of squares are always equal no matter what
A square is another. One cannot cover a larger square with two smaller ones.
I think we should ask, "what other shape doesn't share this property? Does there exist a shape in which a pair of them will cover a larger version of itself?
Contemplate this figure of 3 identical squares:
Here's how two rectangles can cover another that can be slightly larger, per Jeremy's & Linus's suggestions:
And here's what can be done with semicircles:
which can be done with any part of a circle, i.e., even a circle with a tiny slice taken off, leaving a small flat spot on the circumference. So, symmetry seems to be the deciding factor, for convex figures?
With regular hexagons, we seem to run into the same trouble as with squares: