Crazy midpoints!
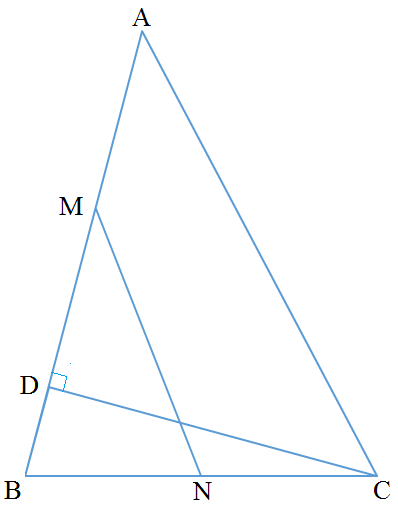
In △ A B C , C D is perpendicular to A B , A B = 8 , C D = 6 , M is midpoint of A D and N is midpoint of B C .
Find the length of M N .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
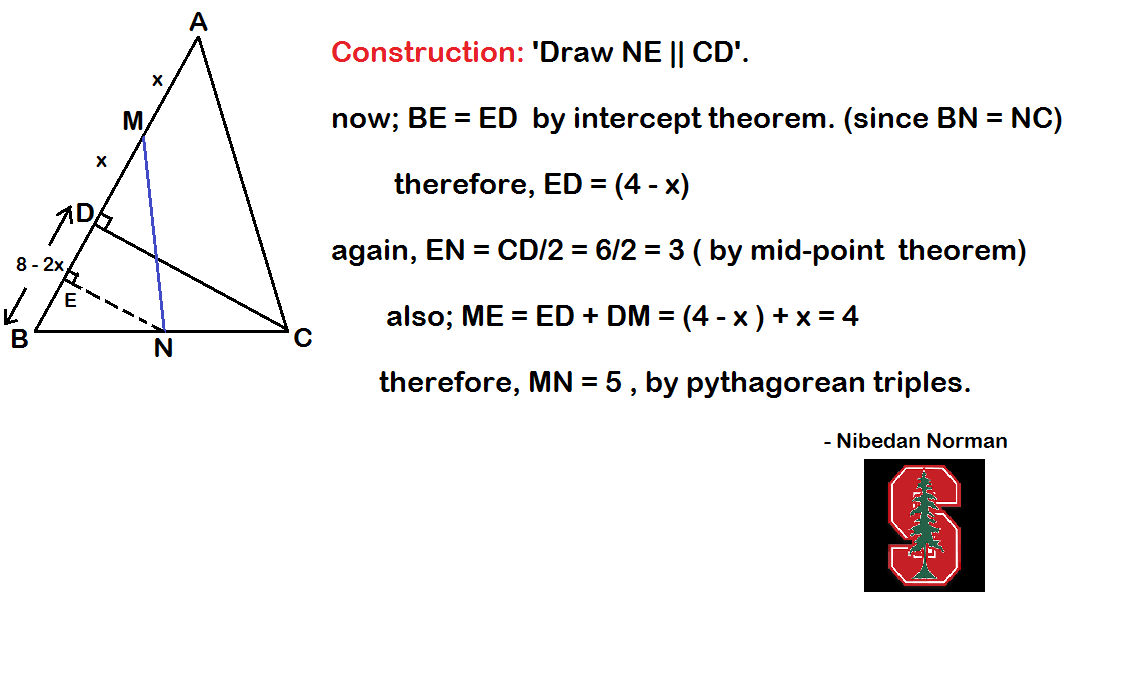
2 doubts : why that image and how do you have 5 upvotes when there are only 4 solvers??
Log in to reply
no. of upvotes are independent of no. of solvers.. a person with wrong answer can also upvote... nd to your last query ... "Its my university editor logo".
Log in to reply
Oh, Solvers mean no. of people who got answer correct. I thought people who attempted.
Log in to reply
@Mr. India – upvoted! your solution.. plz do try to modify your representation (using LATEX, or any other editing tools) ... cheers!
Also you can vote up to 4 votes by clicking on the "Helpful" or the '"Brilliant" icon 4 times in a row.
Log in to reply
helpful, interesting, brilliant, confused... these are the clause of upvote .... (an ML reinforced algorithm instigate with snapping on either of these alternatives)
Is that some technical error? I just tried and it happened.
No, I think it is programmed that way. Bet very few people know about that.
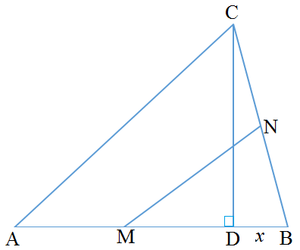
Let D be the origin ( 0 , 0 ) of the x y -plane and B be ( x , 0 ) . Then A ( x − 8 , 0 ) , M ( 2 x − 4 , 0 ) , and N ( 2 x , 3 ) and
M N = ( 2 x − 4 − 2 x ) 2 + ( 0 − 3 ) 2 = 1 6 + 9 = 5
Thank you for editing question!
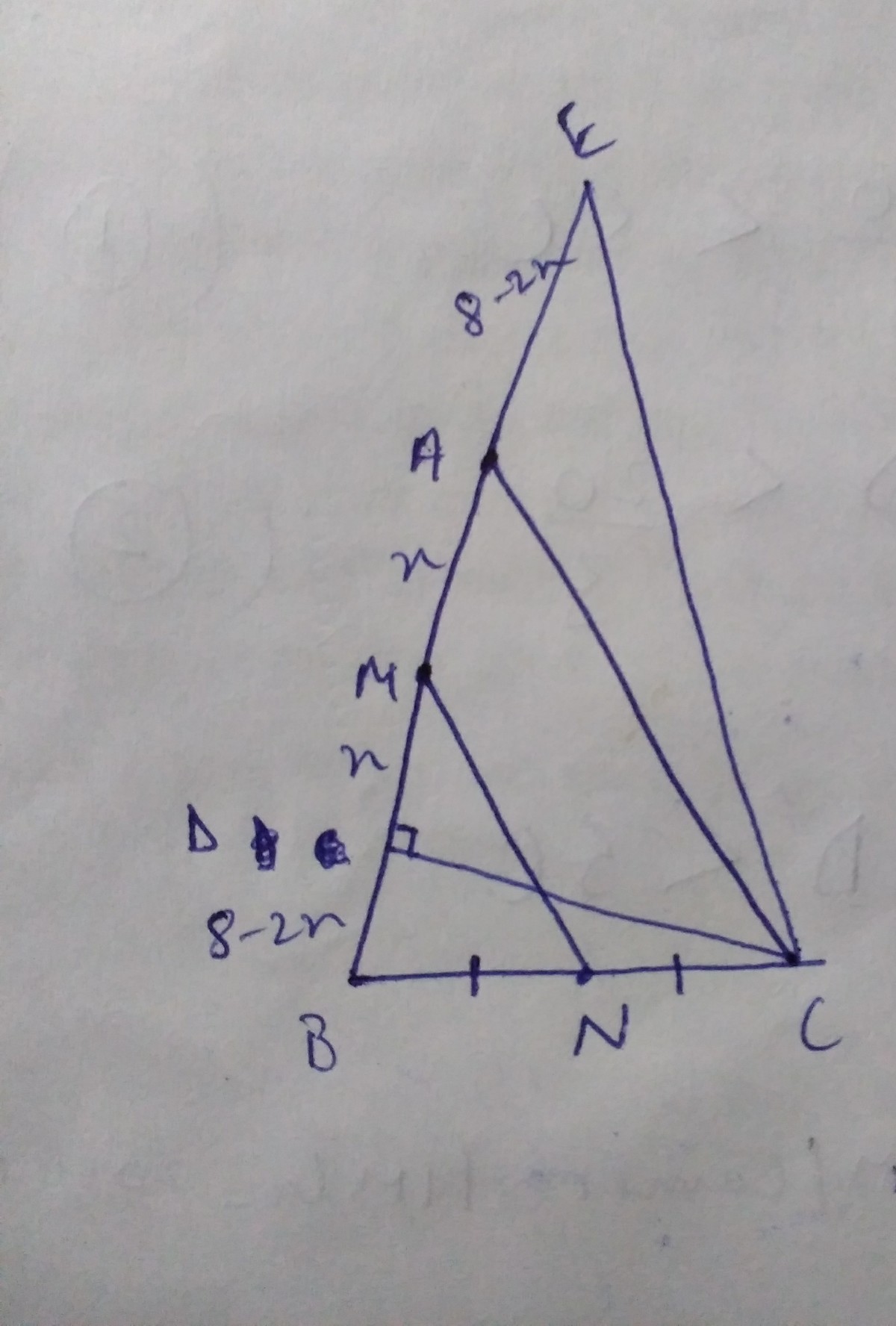
Extend B A to E such that B D = A E
Let A M = M D = x
Then B D = A E = 8 − 2 x ( as A B = 8 c m )
Then M is midpoint of B E as B M = M E = 8 − x
In △ B C E , M and N are midpoints of B E and B C respectively
Therefore, by midpoint theorem 2MN = CE
In △ C D E , D = 9 0 ° , C D = 6 , D E = 8
Therefore, by Pythagoras theorem, C E = 1 0
As 2 M N = C E , M N = 5 c m
This is the 1st problem of the 1993 RMO (Regional Mathematics Olympiad). You can find a link to that here .
Ya you are right. How old are you?
Do you have an aops account?
Log in to reply
No is it good?
Let the position coordinates of A, B and C be (h, k), (0,0) and (a, 0) respectively. Then those of M and N are (ah^2/64, ahk/64) and (a/2,0) respectively. From the given conditions, h^2+k^2=64 and a^2-(ah/8)^2=36. Using these and the distance formula we get the length of MN equal to 5
I actually solved it using coordinate geometry first and then tried geometry (only).!