Crossing Paths in a Space Station
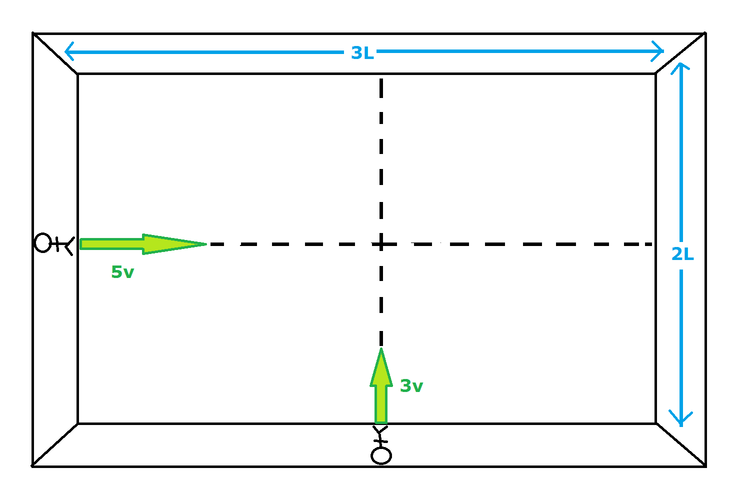 Two astronauts, Alfred and Bob, are positioned at the midpoints of adjacent walls, in a rectangular room, in a space station. Alfred's wall has length
3
L
, and Bob's wall has length
2
L
.
Two astronauts, Alfred and Bob, are positioned at the midpoints of adjacent walls, in a rectangular room, in a space station. Alfred's wall has length
3
L
, and Bob's wall has length
2
L
.
They both push off of their walls at the same instant. Alfred has a speed of 3 v , and Bob has a speed of 5 v . They both stop when they reach their opposing walls.
The closest distance they ever get to each other can be written as a b L , where a and b are positive integers and b is square free.
Find a + b .
Ignore gravity and air resistance.
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice diagrammatic Solution ! :)
We can also solve this by considering (x-y) plane and then using A. O. D
Let the lower-left corner of the room be the origin of our x- y- coordinate system. Then, Alfred and Bob's position vectors, as functions of time, can be written as:
r A ( t ) = < ( 2 3 L ) , ( 3 v t ) > , and r B ( t ) = < ( 5 v t ) , ( L ) >
Then, the displacement vector pointing from Bob to Alfred can be written:
Δ r = < ( 2 3 L − 5 v t ) , ( 3 v t − L ) >
Now we need to minimize the distance. To make the math simpler, we mimimize the square of the distance instead. That is:
r 2 = ( 2 3 L − 5 v t ) 2 + ( 3 v t − L ) 2
and:
d t d r 2 = 2 r d t d r = − 2 1 v L + 6 8 v 2 t
Setting this equal to 0, we can cancel out the 2 r , as I've already verified that r = 0 never occurs. Solving for t , we find that the time of occurence where Alfred and Bob are closest together is:
t = 6 8 v 2 1 L
Now we simply plug this into our distance formula, and simplify to get:
r m i n = 2 3 4 L
So, a + b = 3 6
I guess it would be simpler if we solved the problem in the frame of one of the astronauts, (say Alfred.) Bob will appear to move in a straight line, and the shortest distance between them will be when the line joining Alfred and Bob would be perpendicular to the Bob's path.
 q
q
The length of the perpendicular can be easily calculated by using base x height = perpendicular x hypotenuse.
Nice solution, Tyler. One typo to point out, however; in the line where you take derivatives you should have − 2 1 v L + 6 8 v 2 t . Perhaps you could also expand d t d r 2 as 2 r d t d r , but that's just a personal preference.
Log in to reply
d=rt , t=d/r, Bob's time to get to center of the room = 1.5 L/ 5v. At that instance Alfred is (1.5L/5v )* 3v = .9 L from his take-off point or 0.1 L from the center of the room, where Alfred is. At times before this and after this the distances between them are greater. Therefore I claim that L/10 is the closest distance they get to each other.
What is incorrect about my analysis?
Log in to reply
I agree that for the times before this the distance is greater than 1 0 L , but for a short interval after this the distance between the two diminishes further. As a demonstration, reset to clock to zero when Bob reaches the center of the room, and for convenience let L = 1 0 , v = 1 . Then the distance between the two after time T is
( 5 T ) 2 + ( 1 − 3 T ) 2 = 3 4 T 2 − 6 T + 1 = T ( 3 4 T − 6 ) + 1 ,
which will be less than 1 0 L = 1 when 0 ≤ T ≤ 3 4 6 .
So for any L , v there will be a brief interval in which the two astronauts are closer than 1 0 L , and Tyler's analysis identifies the time at which they are closest.
Log in to reply
@Brian Charlesworth – Thanks for the enlightenment, Charles. I accept this now, had to prove it to myself with diagrams. I must say that the concept is counter-intuitive, though. Who'd a thunk it!
Log in to reply
@Guiseppi Butel – Yes, I agree that it is counter-intuitive. I actually made the above sample calculation to convince myself that the solution obtained using calculus was in fact reasonable. :)
Thanks for pointing out the typo. I'll probably change the derivative notation as well.
Log in to reply
You're welcome. It was a nice twist putting astronauts into your problem. A follow-up question could look at the scenario where they don't stop after hitting the opposite walls and just keep bouncing back and forth until they actually collide. The question would then be whether or not they will ever collide, and if they do, after what time will the collision occur.
Log in to reply
@Brian Charlesworth – You read my mind.
Log in to reply
@Tyler Hanna – Haha. Well, with the two bouncing back and forth, Alfred will be at the center of the rectangle at times
t A = 1 0 v 3 L + n ∗ 5 v 3 L
for integers n ≥ 0 and Bob will be at the center at times
t B = 3 v L + m ∗ 3 v 2 L .
for integers m ≥ 0 . For the two of them to collide we would need t A = t B for some m , n . Equating and simplifying, this would require that there exist m , n such that
1 8 n − 2 0 m = 1 ,
which, since g cd ( 1 8 , 2 0 ) = 2 , has so integer solution, (as 2 is the least integer that can be written in this form). Thus Alfred and Bob will never collide.
So the next question is whether they will ever get closer than they do on the first pass. I'll get to those calculations... sometime. :)
Log in to reply
@Brian Charlesworth – I'll probably redo the problem with different numbers so that they do collide, but first I've got a center of mass problem that I've been working on for three days now, so I should probably get that one up first.
Best Technique To Solve This Problem is By using Concept of Relative Motion
Let us Consider our Refrence frame at B (Say Bob) , Then in this frame B is at rest , So
Equation of motion of A (Alfred) is a straight Line Motion w.r.t Bob (B) So it's equation is :
y − 0 = 5 − 3 ( x − 2 3 L ) 3 x + 5 y = 2 9 L .
Closest Distance between them is equal to Perpendicular distance of (bob) B(0,L) from the Line which is :
d m i n = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 3 2 + 5 2 0 + 5 L − 2 9 L ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ d m i n = 2 3 4 L .