Cryptogram: product of two positive integer giving a third positive integer.
× A A B A B C C B C B D A E C C F D A
What is the product? Computer solutions are acceptable.
Note: Each letter denotes a distinct single-digit integer and A and B are nonzero.
The above note was not added by the problem's auther; rather, it was added by a Brilliant moderator.
The answer is 409311809.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Exactly! That is a form of "exhaustive computer" similar to what I used in a different language, which contained the check for non-duplication of codes directly, and which used the fact that some of the code were leading digits and therefore could not be one.
" Note: Each letter denotes a distinct single-digit integer and A and B are nonzero." is the specification that D and E are not equal.
Log in to reply
I actually can add in the codes to check the each letter denotes a distinct digit. But since there are only two outcomes manual checking is easy. You should post your code whatever language it is. I added "Note: Each letter denotes a distinct single-digit integer and A and B are nonzero." for you. I am a moderator.
Log in to reply
The reason for not posting the program as originally written is that the original language is not one the Brilliant supports.
I amended my original solution to provide a solution program written in C.
Could Brilliant support Ruby or Java in their coding environment? I prefer to use on Brilliant only languages that others could re-enter and try for themselves.
Here is the solution in its original form (it is a single line of code)(it is not written in a Brilliant supported language):
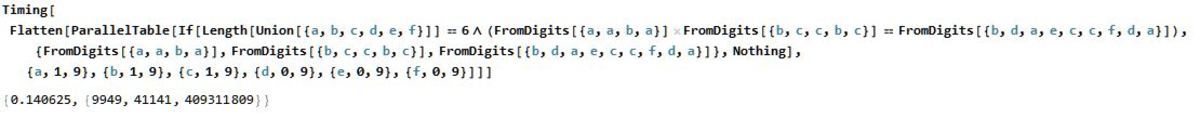
Altogether, the development and solution runs in under a third of a second.
Log in to reply
@A Former Brilliant Member – Jane, just print screen your code and paste here just like I did.
Log in to reply
@Chew-Seong Cheong – I had posted the solution program in C and the original language. Brilliant's input processing mangled the single line of code. I replaced it, per your request, with an image.
Log in to reply
@A Former Brilliant Member – You can add it to your solution posted.
9 9 4 9 × 4 1 1 4 1 = 4 0 9 3 1 1 8 0 9
Since both the multiplicand and the multiplier are primes and their order is specified by their digit length, the product is unique.
Nonetheless, the answer is verified by exhaustive computer search.
The solution in a language that Brilliant supports, C:

The program's output:
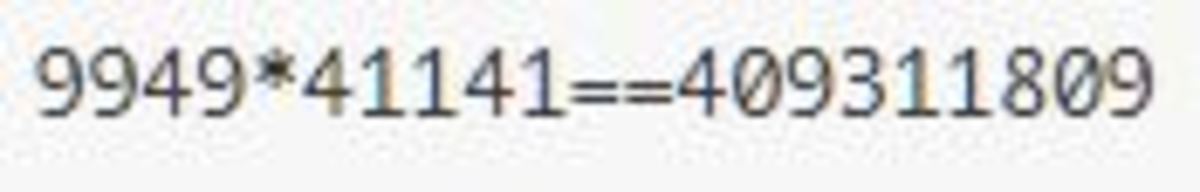
The original solution ( a single line of code):
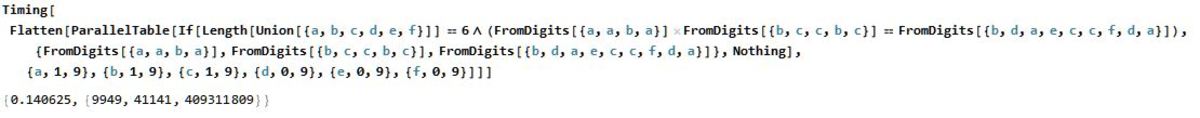
@Jane Doe , I have amended the problem for you. We have to mention the letters denote different digits, else we would have two solutions.
" Note: Each letter denotes a distinct single-digit integer and A and B are nonzero." is the specification that D and E are not equal.
Log in to reply
In cryptograms, unless stated otherwise, that note is the normal conventions. In the future, please, note that such amendments were added by a moderator.
Using Python with coding environment of Brilliant.org:
From the code, there are two solutions, but 3 0 9 4 1 1 0 0 9 has D = E therefore not acceptable. The solution is 4 0 9 3 1 1 8 0 9 .