Cryptogram Sum
+ A C E B D F
In the above cryptogram, all the letters represent distinct digits.
What is the minimum possible value of the 2-digit integer E F ?
Note: In cryptogram problems, 0 is not allowed to be a leading (first) digit, since we would just not write anything in its place.
The answer is 39.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Moderator note:
Out of the 476 solutions for this puzzle (not considering the issue of which sum is smallest), 76 of them involve a digit 0, but it can only be placed at F . Do you see why?
Note: A very common mistake made is to only ensure that A, B, C, and D are distinct. Many people forgot to check that E and F also need to be distinct from the rest. If you obtained the answer of 33, note then that E = F = 3 are not distinct values.
Why can't any digit be a zero? I assumed no leading zero, but why not in the ones position?
Log in to reply
Good question. Let's develop that train of thought further.
Suppose that B is 0. Would D and F be distinct?
Suppose that D is 0. Would B and F be distinct?
Suppose that F is 0. Would B and D be distinct?
Log in to reply
F could certainly be zero if B + D = 10. But with A, C distinct that would mean the sum would have to be at least 40. (For example 13 + 27).
Log in to reply
@Richard Desper – As the challenge note points out, there are 76 solutions where F = 0. (Jacob's solution incorrectly states none of the digits can be 0.)
@Richard Desper – Indeed! I was illustrating the path that one could take to further develop the thought of "why can't any digit be a zero"?
Sometimes, breaking up a complicated problem into the various components is much easier to handle. IE Checking cases.
For such cryptogram problems, 0 is never allowed as a leading digit.
I have edited this into the problem. Those who previously answered 23 have been marked correct. I have deleted comments relating to the leading digit.
Where did you get the number 476? If that's too complicated/long of an answer for this message board, do you maybe have a reference to the combinatorics theory behind summation of unique digits like this? Or is it a well known solution?
Log in to reply
I am unaware of a general theory behind this. (How might one generalize this problem? That's a good question. We could check A+B=C, AB+CD=EF, and ABC+DEF=GHI, but past that point we can't have distinct digits any more.)
The general problem is fairly involved for a comment, but let's just count the ways of getting F = 0. That means BD is from {19, 28, 37, 46} and ACE is from the set {124, 136, 146, 157, 168, 179, 236, 247, 258, 269, 348, 359}. Then taking each from the first set and counting how many don't clash with unique digits from the second set gives 4 + 5 + 5 + 5 = 19, and the digits can be reversed in either case so the total needs to be multiplied by 4 (that is: normal-normal, reversed-normal, normal-reversed, reversed-reversed), giving a total of 19 * 4 = 76.
A-1 b-0 c-2 d-3 .. total is 33 .. ef .. then 33 is the lowest right ?? Wtf
I do not understand the definition of "distinct", nor do I understand why we cannot have a leading "0". If that is the case, these conditions should have been clearly added to the statement of the problem. As far as I am concerned, the correct answer is "23".
Log in to reply
These conditions are in the problem statement.
Distinct means that the numbers represented by different values are different. You implicitly used that to obtain the answer of 23.
Log in to reply
Those conditions were NOT in the statement I saw. And my question about "distinct" came from the statement by Jacob Mercier : "All digits are distinct therefore none can be 0."
Log in to reply
- Can you link me to where the condition of distinct was not stated? If this is done in error, I would like to fix it. On both the site and facebook post, it is stated "each letter represents a distinct digit". Besides, this is also a standard context of cryptogram problems.
Your comment was with regards to "why we cannot have a leading 0". Even though this is also a standard context of cryptogram problems, it was subsequently added to the problem as several people had that confusion. It was intentionally added to our facebook post made yesterday, but it is not a standard disclaimer that we state.
I admit that this solution isn't completely correct, nor adequately explained. Let me edit it further for clarity. In particular, please read the Challenge Master note.
Note: The reason why these conditions are automatically assumed in cryptogram problems, is so that cryptogram doesn't admit the trivial solution of
+ 0 0 0 0 0 0
For reference, this is our FB post. The conditions are listed in the message.

Log in to reply
@Calvin Lin – I agree that this post is clear. But the earlier posted version did not say anything about not having leading 0. The "implicit" rules of cryptograms are not very useful to me, since I am a relative newcomer.
I totally agree with George and Setyo. This is not a well stated problem at all . Why should I assume that you assume that the leading digit is a not allowed to be a 0. Also I might assume that other digest may be allowed But not noted. AB =69 BC = 32 EF =01. Very badly put question. It is very difficult to understand how this question ever got selected for the problem of the week.
10+23 satisfies all ideal conditions in mathematics so 33 should be it.
Log in to reply
What is E and F? Are they distinct from all the other digits?
I'm totally confused. The question was what is the smallest value for 2-EF. That would be 96.
Log in to reply
How did you determine that the smallest value is 96?
Notice that 14+25=39, showing that 39 can be achieved.
As pointed out, the parameters didn't exclude 0 from being in the ones column; only from being a leading digit. That would open the possibility to having a 10 and a 23 for the distinct digits. Yielding 33 as the lowest sum.
Log in to reply
It can't be 33 as they are not distinct. I thought 33 too until I reread the problem
if you use 10 + 23 = 33. that would be D=3 and F = 3. They have to be distinct. Even though they don't exclude 0 from being in the one's column, that is why the correct answer doesn't involve a 0.
Using unique negative values the minimum possible is -99
Log in to reply
A digit is any of the numerals from 0 to 9, this doesn't allow the placement of negative numbers.
Log in to reply
(I realize this is a puzzle not a semantics exercise) The puzzle states "2-digit integer" Integers can be positive or negative, digit refers to a number of Arabic characters (assuming base ten.) It was not stated that each digit had to be a Natural number, which is a smaller subset. Negative numbers can have digits. Using the word Integer, includes negative numbers.
Log in to reply
@Jim Burke – While I understand your frustration, as with all problems, we are going by the standard rules of the context. If we had to define explicitly what every single term meant, then we would never be done (E.g. What is positive? What is a digit? What is a number?). In addition, this also ensures that the problem doesn't result in "1 + 1 = 10 because we are doing binary addition without telling you".
Log in to reply
@Calvin Lin – I agree, we do make reasonable assumptions, however the words used here led to and allowed for the solution with out Martian Mathematics. The standard context used is consistent with similar solutions used in engineering, it is a common assumption to say digits have to be positive since young people grew up with digital displays ect - 'digit' is a mathematical term. I won't comment further - I appreciate all you do to make this possible.
Log in to reply
@Jim Burke – Digits are neither positive nor negative. Numbers can be negative. Digits are the symbols {1,2,3,4,5,6,7,8,9,0}. That is the standard definition.
The problem must be stated more clearly. Explaining the "leading" definition of a possible number.
Log in to reply
I think this is a standard term. I've added "(first)" just in case.
Agree, the problem did not not exclude 0, it only stipulated that 0 could not be a leading digit. Using those rules, I get 10+23=34
The answer should be 33 and not 39. The question mentions not to use leading 0s. However, we can still use the 0 as the trailing digit and 10 is a valid two-digit integer. So, we can have A = 1, B = 0, C = 2 and D = 3. So, it should be 10 + 23 = 33. This question seems to be wrong.
Log in to reply
In your solution 3 is coming three times D=3, E=3 and F=3.
If B=0, then D=F, (or) If D=0, then B=F.
If F=0, then E>3 so it will be more than our minimum 39.
Thank you Arpan....I came up with 33 also and couldn't see why 39 was the right answer
Log in to reply
33 is not the correct answer It is violating the condition all digits are distinct. If you use "0" in the once place you will get the following issue.
If B=0, then D=F, (or) If D=0, then B=F.
If F=0, then E>3 so it will be more than our minimum 39.
The set of all integers includes negative numbers, right?
Log in to reply
While I understand your frustration with the definition, as with all problems, we are going by the standard rules of the context (of cryptograms). All the digits are non-negative. If we had to define explicitly what every single term meant, then we would never be done (E.g. What is positive? What is a digit? What is a number?). In addition, this also ensures that the problem doesn't result in "1 + 1 = 10 because we are doing binary addition without telling you".
In the problem, it is stated clearly A,B,C,D,E, F represent distinct digits and 0 is not allowed to be a leading digit. That means you need to find the solution using 1,2,3,...,9.
Log in to reply
So if a puzzle you just made up excludes 0 then it necessarily follows that it also excludes negative numbers, is that the rule ?
Log in to reply
@Phil Southgate – where is the negative sign? Problem all about distinct digits addition not about integer values. It is not possible (A=1 and B= -5)
Where was "0" not allowed? Where was it not allowed as a leading digit? 06 + 25 = 31 all distinct.
Log in to reply
and then it gets smaller where 16+07=23
Log in to reply
Please read the problem statement carefully. In the "Note" it is mentioned "In cryptogram problems, 0 is not allowed to be a leading digit, since we would just not write anything in its place." Based on that I posted my solution and also posted the same note in the solution.
A and C can be either 1 or 2 . B or D cannot be 3 since the sum of A and C is 3 . So B and D can be either 4 or 5 .
Be careful with presenting the logical reasoning for such questions. It is not be guaranteed that E = 3 , since we might have had a carry over.
Nice trap! (I answered "37" and then "33", but "3" was already among C,D!)
Question is incomplete
according to my view answer is 20 which is the minimum number. 10 + 10 = 20. and maximum is 99.
Log in to reply
What is B and D? Are they distinct from each other?
Log in to reply
oh thank you very much. I didn't focus on the distinct part. I was focused on the minimum I didn't see the distinct condition. sorry. :)
A=6, B=4, C=3, D=7, therefore E&F = 01, the smallest positive 2-digit integer with distinct digits. Sure there exists a 1 (or F) to the left of EF, but the question is the minimum possible value of the 2-digit integer EF.
Log in to reply
In that case, the cryptogram isn't of the form that is given.
If you were to do true crypto-arithmetic ... it would be modulo arithmetic where the carry value is tossed away. If we were to do this using modulo-10 arithmetic, the correct answer would be 12 ... 60 + 52 = 12 ... since the 100 is a carry by 1 ... this value gets tossed away. This is how the arithmetic is done for crypto. This is also why prime numbers are very important in this arena.
Log in to reply
Do you have a link which substantiates that " true crypto-arithmetic ... it would be modulo arithmetic where the carry value is tossed away"? This is the first time I've heard about it.
Log in to reply
To tell you the truth ... my answer was incorrect. The correct answer is 10 modulo 10. The substantiation with modulo arithmetic has really to do with the implementation. In computors and with the very 1st crypto machines, (aka bombe), the registers or the computation wheels always did the arithmetic with respect to some modulus. In that you had a limited set of wheels,or in the computer, you have some limit to the number of bits that you will use to represent the numbers. In computer arithmetic. When the arithmetic would over flow, the carry bit is virtual ... This results in the most significant bit being "tossed away". So ... there really is no exact theoretical basis for this ... it really is the result of the practical limits to any form of computing.
As you see, the original poster did not say what the storage limit for the numerical value is. He implied this value by saying that leading zeroes were not allowed. With machines, leading zeroes are allowed ... up to the limit of the size of the registers used for the computation. In reality, in a computer, these numbers would not be calculated ala modulo-10. They probably would be calculated as some large modulo.... most likely modulo 2^32 or modulo 4 billion or thereabouts ... or in the newer machines as modulo 2^64 ... or if we use AES128, (128-bit encryption), it would be modulo 2^128.
I hope this clarifies this. I am talking about encryption mathematics vs. the implementation of the math. But in general ... most encryption revolves around modulo arithmetic. You can even see the rotational architecture in a picture here in Wikipedia. https://en.wikipedia.org/wiki/Bombe
The obvious solution is 14+25 = 39 since zero cannot be used; or can it? Zero cannot be used for ABC or D because using zero in any of those positions would result in a duplicate digit for either E or F (zero is the identity element for addition). However if we use zero for F, we still have unique digits everywhere and no leading zeros. To accomplish this, we have 14 + 26 = 40. This is still larger than 39, so it's not the answer.
AB+CD=B+D+10(A+C) , to minimize it A and C is minimum A,C=1,2 then guess B,D from 3,4 or 4,5 or 5,6 the 4,5 will give distinct digit so answer is 5+4+10(1+2)=39 :)
Really nice problem. The question does not state that leading zeroes are not allowed. If one is used then 04+19=23 is a better solution. I think either the correct answer should be 23 or the question should state that leading zeroes are not allowed.
Zero can’t be the first digit but it can be the second. So if A-1, B-0, C-2 and D-3 it would be 33. That’s is the smallest you can go.
I have 23 14 = 37. I must not be understanding the question :/
0 is a digit, for God's sake!
Log in to reply
Yes, 0 is a digit. What solution of yours uses distinct digits and a 0?
"Note: In cryptogram problems, 0 is not allowed to be a leading digit, since we would just not write anything in its place." So you can assume it can be the second digit. So 13 + 20 = 33. If leading digits were allowed it could be 03 + 12 = 15.
Log in to reply
For 13 + 20 = 33, what are E and F? Are they distinct?
For 03 + 12 = 15, what are C and E? Are they distinct?
0 can't be the leading digit, so A=1,C=2 therefore E Must be 3. As all digits are distinct, B=0 and D=4 (neither can be 3 as we have determined E=3). With all criteria, satisfied the answer has to be 34. Certainly can't be 33 as some subscribers maintain because ALL digits are distinct. 34 is the answer to satisfy the criteria.
Log in to reply
34 doesnt satisfy the question because D and F are not distinct
Why is the answer not 37? A=1, B=3, C=2, D=4. Each distinct, totals 37
Log in to reply
What are E and F? Are all digits A, B, C, D, E, F distinct?
This is my second attempt at this question after awhile and I got it wrong again because the instructions are not clear. I got -85. A=1, B=2, C= -9, D=7, EF= - 85 All different integers
Log in to reply
You are not allowed to use negative numbers in cryptograms.
Note: If the problem allowed for negative numbers, then you could get − 2 3 − 7 5 = − 9 8 .
For such cryptogram problems, 0 is never allowed as a leading digit.
I have edited this into the problem.
If zero is considered a digit, it could be used in either the B or D position, so the answer then would be 34. A=1, B=0, C=2, D=4 since 3 could not be used. My mistake; 4 is repeated with D and F, so D has to be 5 with the answer being 39.
Nothing in the problem limits the values to positive digits. I think the minimum is -98. A = -4, B = -7, C = -5, D = -1.
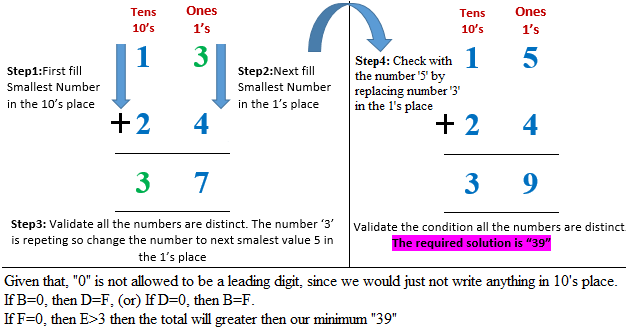
All digits are distinct therefore none can be 0. (Edit: Note that this claim is not true. It is possible for F to be 0. However, it is not possible for B (or D) to be 0, since that would then imply that D = F (resp B = F . See the Challenge Master note for more details)
For the smallest EF, smallest E is a priority, as it is an order of magnitude larger. Therefore A & C should take 1 & 2, making E 3, and B & D take the next two smallest distinct non zero digits, 4 & 5, giving EF = 39.