Crystal Movement
Can we color the edges of the octahedron above without lifting the pencil nor coloring the same edge more than once?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
the statement of the theorem says "if and only if"..it's necessary to show the path?
Log in to reply
no, you can color all the horizontal edges first, then the up and downs. When it says only and only if, it's talking about the conditions for it ending on the same point, not the path it needs to take
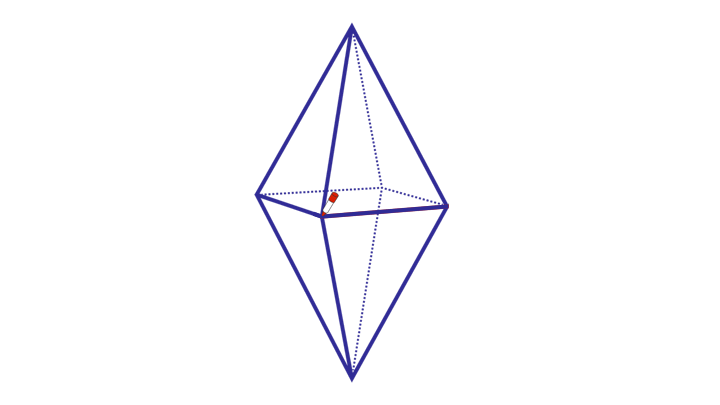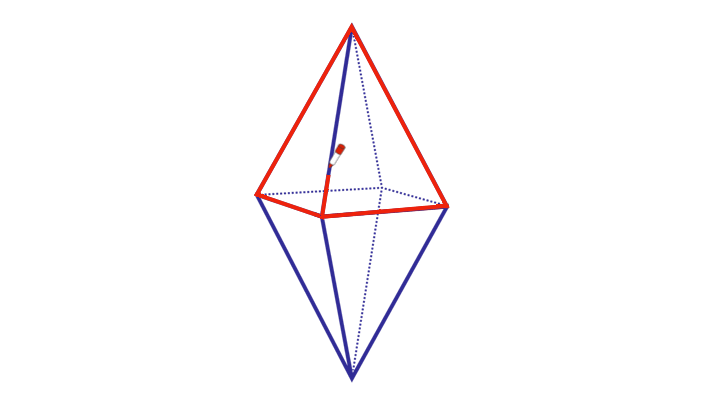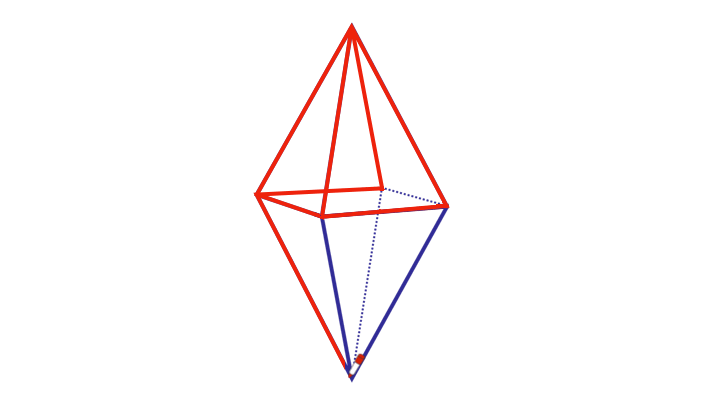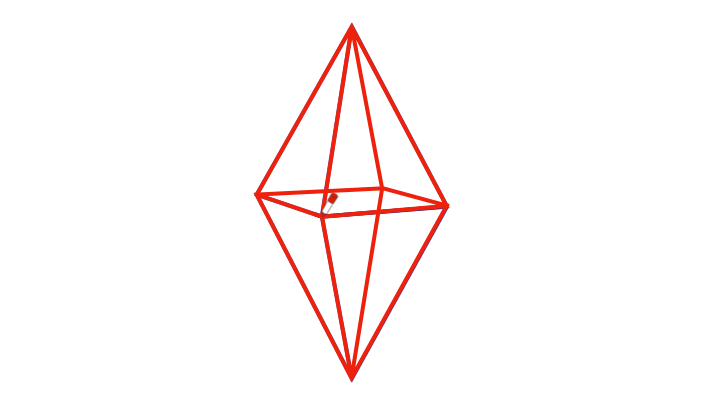
Log in to reply
no, you can color all the horizontal edges first, then the up and downs. When it says only and only if, it's talking about the conditions for it ending on the same point, not the path it needs to take
Log in to reply
The question simply asks "Can we color the edges of the octahedron above without lifting the pencil nor coloring the same edge more than once?" And anyways, I've shown a way, so it's possible.
Log in to reply
@Mahdi Raza – but you use a pen/color pastel on a gif, not a pencil :D
O, sorry, I meant to reply to the comment above your post
It's because each corner has 4 sides coming off it, which is an even number. It doesn't work with a cube because a cube has 3 sides coming off each corner so the lines end at the corners.
For me, it is a logic... we can color each edges by rotating your screen and we can color it downward. Lol
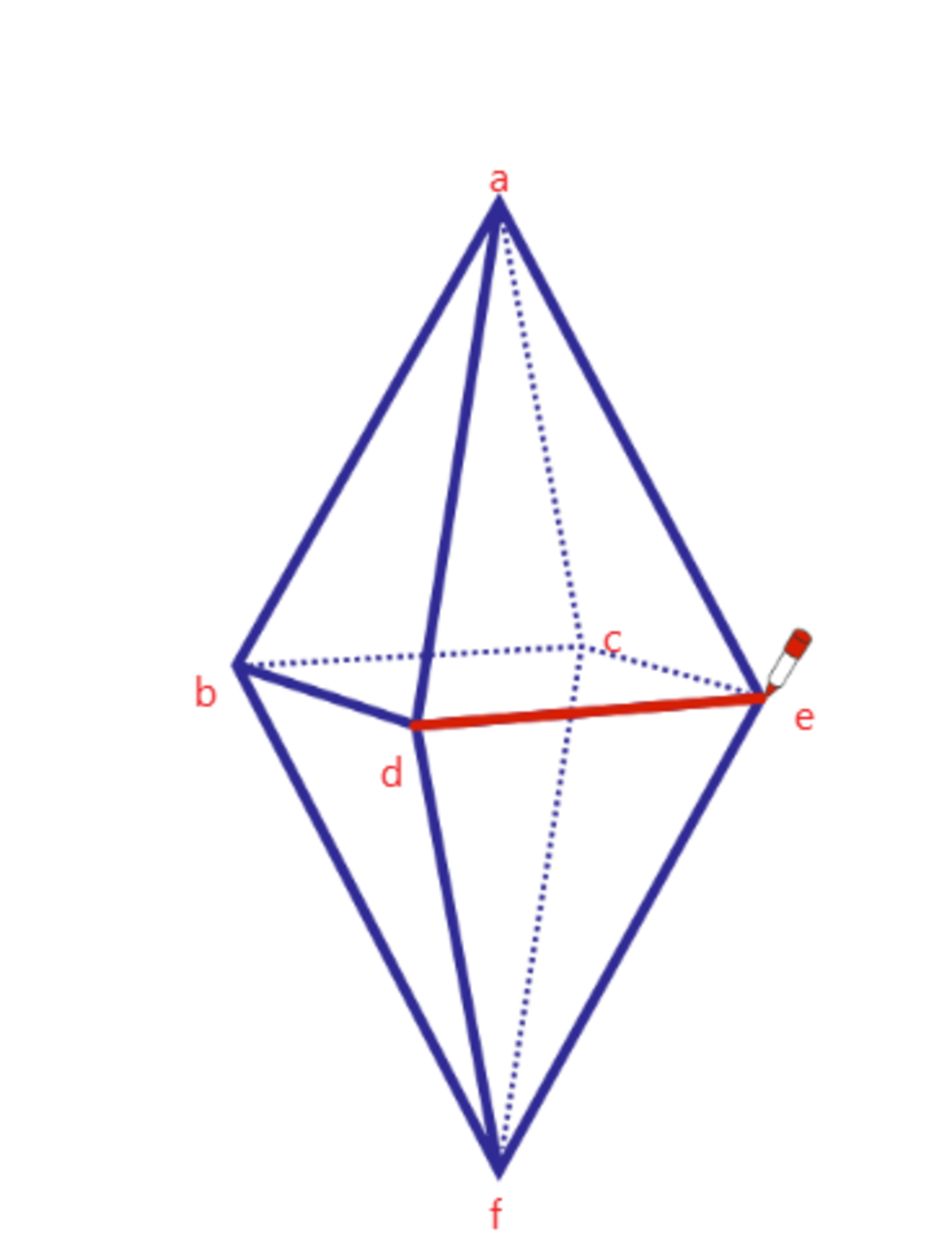 If we mark the vertexes from the given figure then we will see;
Vertex
a
has
4
degrees,
Vertex
b
has
4
degrees,
Vertex
c
has
4
degrees,
Vertex
d
has
4
degrees,
Vertex
e
has
4
degrees,
Vertex
f
has
4
degrees.
If we mark the vertexes from the given figure then we will see;
Vertex
a
has
4
degrees,
Vertex
b
has
4
degrees,
Vertex
c
has
4
degrees,
Vertex
d
has
4
degrees,
Vertex
e
has
4
degrees,
Vertex
f
has
4
degrees.
As all of the vertexes has even no of degrees, then according to Euler's law it has both Eulerian path & circuit. So, we can color the edges of the octahedron above without lifting the pencil nor coloring the same edge more than once
Why is this the only Eulerian proof???
If we plot the vertices of the octahedron as nodes of the graph, we will acquire 6 nodes, each with a degree of 4 , and the Eulerian path can be drawn as shown below:
In theory, if all nodes have even degrees (4 connections to other nodes in this case), the graph will be an Eulerian cycle : the path can be drawn without repeating the edges and returning to the starting point.