Cube Corner Classic
A particle of mass
is placed at one of the corners of cube(
of
uniformly distributed over the volume)of side
. Find the velocity required by that particle to escape from that cube's gravitational field forever.
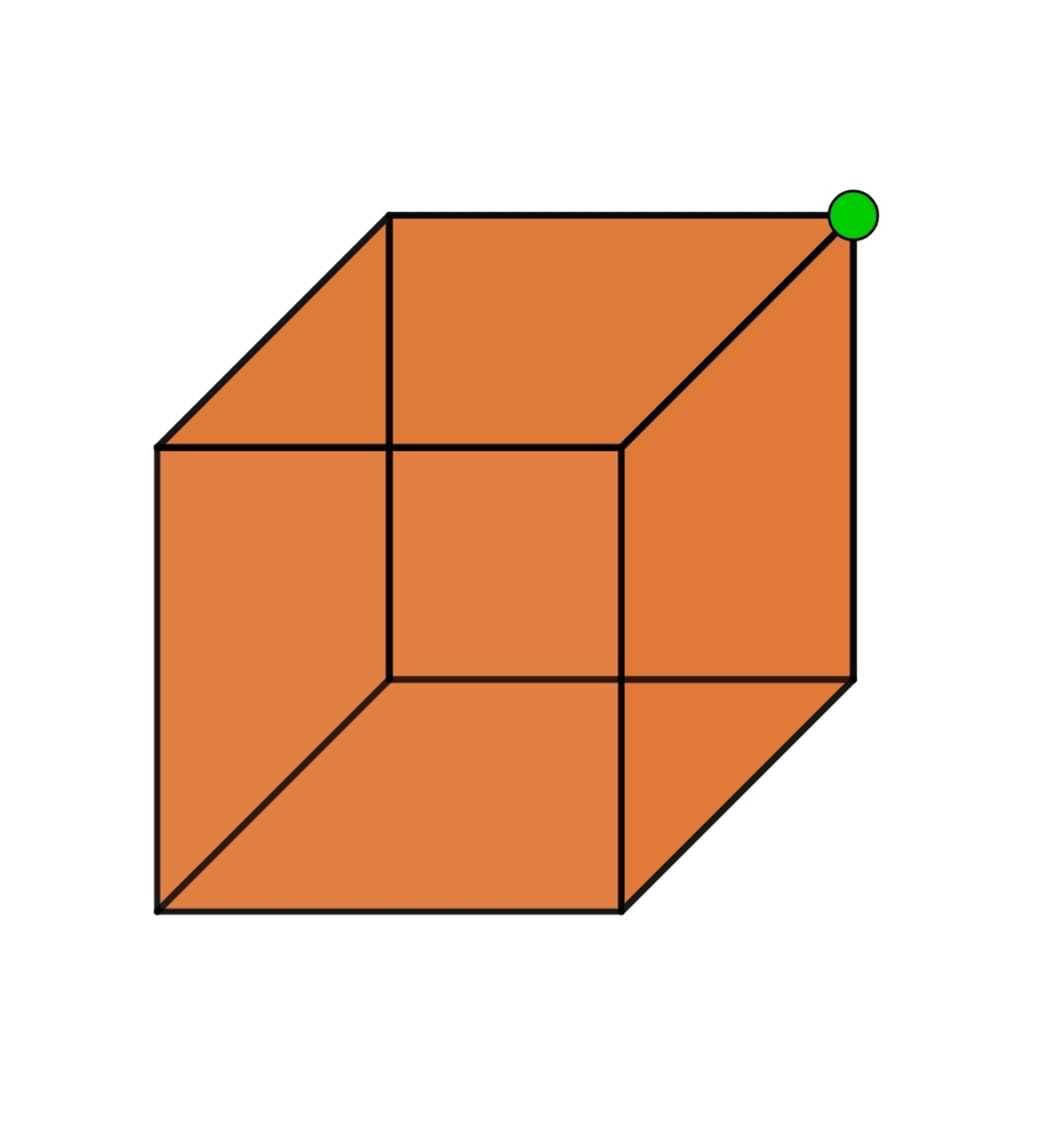Take
(for simplicity)
The answer is 48.786.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Potential energy of the ball and cube is 1000/√((x-1)^2+(y-1)^2+(z-1)^2)dxdydz Integrate from (x=0 to x=1)(y=0 to y=1)(z=0toz=1) On integrating we get ∆U=1190.04 (1/2)v^2=1190.04 V=48.786
But sorry For inconvinience as i dont know how to write math expressions here it will be good if anyone teaches me