Cube Lattice Path Tilings
An NEU path (North, East, and Up path) in 3-D is a sequence of cubes, where each successive cube is either 1 unit north, east, or up. When represented as lattice points in Z 3 , the steps have size ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) or ( 0 , 0 , 1 ) .
The goal is to tile a 2 7 × 2 7 × 2 7 cube using NEU paths which fit entirely within the cube and do not overlap each other. What is the fewest number of NEU paths that are needed?
An NEU path tiling of a
3
×
3
×
3
cube with 7 paths (paths 6 and 7 are hidden from view)
As an explicit example, the minimal tiling of a 3 × 3 × 3 cube with NEU paths requires 7 paths. An example is shown to the right, but 2 paths are hidden from view.
The answer is 547.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This analysis works for a cube with (2n+1) "blocks" on a side. For a 27x27x27 cube, n=13, not 7! I came up with an explicit procedure that reduced an NxNxN cube to a (N-2)x(N-2)x(N-2) cube in 3(n-1) steps. For N = 2n+1, iteration down to n = 0 (a single block that is removed in one step) gives the same expression as above. This proves that this is an upper bound on the number of required steps. The 1st and 3rd parts of the above argument show that the number cannot be less than 3n(n+1)+1.
My "construction". Label the faces x,y,z. Step 1: For each value of z remove blocks with minimum values of y and then maximum values of x. This uses paths and leaves you with a (n-1)x(n-1)xn block (I will label size in x,y,z directions respectively). Now for each (n-1) value of x, remove blocks with minimum y values and then maximum z values. This gives a (n-1)x(n-2)x(n-1) block. Now for each value of y, remove minimum z values and then maximum x values with (n-2) paths. This leaves one with an (n-2)x(n-2)x(n-2) block and took 3(n-1) steps.
Log in to reply
I never used n = 7 . I used n = 3 as an example of how the injection works. I used n = 1 3 in my final calculation.
As I understand it, you use 2 n + 1 EU paths to cover the bottom and right faces, then 2 n UN paths to cover the remainder of the front and top faces, then 2 n − 1 NE paths to cover the remainder of the left and back faces. Thus 6 n NEU paths cover the outer shell of the cube of side 2 n + 1 , leaving the interior cube of side 2 n − 1 to fill. By induction, the whole cube of side 2 n + 1 can be covered by 1 + 6 ∑ j = 1 n j = 3 n 2 + 3 n + 1 paths. Nice! Then we use my fact that we need at least ∣ S n , 0 ∣ paths, and we are done.
Note: It is not sufficient for "It is clear that each vertex in S n , 1 can be reached from a vertex in S n , 0 by a valid move". As an extreme example, if the vertices in S n , 1 were all only connected to 1 particular vertex in S n , 0 , then even though your condition is satisfied, we cannot create the distinct NEU paths.
This is why we need the perfect matching in my argument, to ensure that we can map distinct tiles to distinct tiles.
Log in to reply
For any 1 ≤ j ≤ 3 n , there exists an injection f j from S n , j to S n , j − 1 such that any vertex v can be reached from f j ( v ) by a valid move. That makes the extension of paths possible. I will post details later (after moving house).
Log in to reply
Indeed, the existence of the injection is important.
I'm amazed that you found such a simple description of it :)
Log in to reply
@Calvin Lin – To be honest, so am I. To see what it was operationally was quite straightforward, but describing it algebraically was initially very complex. Then I noticed the cute final expression. :)
I think that answers your point...
Treat the elements of { 1 , 2 , 3 , … , n } 3 as a poset with relation ≤ , defined as follows. ( a , b , c ) ≤ ( x , y , z ) exactly if all of these are true: i) a ≤ x , ii) b ≤ y , and iii) c ≤ z . Note that this means there exists a NEU path from ( a , b , c ) to ( x , y , z ) .
A NEU path is a chain of elements in this poset. We're looking to cover the whole poset with chains. By Dilworth's theorem, the minimum number of chains required is equal to the size of the largest antichain. So we only need to find the size of the largest antichain in this poset.
...unfortunately, I'm not very certain how to do that. I only remember that the largest antichain is a "slice" of a hexagon of the cube; one of the largest antichains is formed by the elements ( x , y , z ) satisfying x + y + z = ⌊ 2 3 n + 3 ⌋ , but I forgot the proof that this is the largest possible. (It's easy to prove that it is indeed an antichain, though. Also, the only other largest antichain is for ( x , y , z ) satisfying ⌈ 2 3 n + 3 ⌉ . For odd n the two are identical, so the largest antichain is unique.)
The number of elements in this antichain can be easily computed, however. Define k = ⌊ 2 3 n + 3 ⌋ . We're looking for the number of integral solutions to x + y + z = k , where 1 ≤ x , y , z ≤ n . One way to do it is to compute the number of solutions to this equation when 1 ≤ x , y , z (not caring about the upper bound), call this A ; and then subtract it with the number of solutions to this equation where some of x , y , z is greater than n , call this B .
A can be computed by standard stars-and-bars technique application, giving ( 2 k − 1 ) solutions. B , fortunately, can be computed easily too: if there are two of x , y , z that are greater than n , then x + y + z ≥ ( n + 1 ) + ( n + 1 ) + 1 = 2 n + 3 > k , so it's impossible to have x + y + z = k . Thus exactly one of x , y , z is greater than n . We may as well assume it's x , and remember to multiply the result by 3 to obtain B . Now, substitute x ′ = x − n , so that x ′ + y + z = k − n with x ′ , y , z ≥ 1 ; this has ( 2 k − n − 1 ) solutions. So B = 3 ( 2 k − n − 1 ) solutions, and finally our desired number, the number of elements in the antichain, is A − B = ( 2 k − 1 ) − 3 ( 2 k − n − 1 ) .
For this problem, we have n = 2 7 , so k = 4 2 . Substituting, we get ( 2 4 1 ) − 3 ( 2 1 4 ) = 5 4 7 elements in the antichain; by Dilworth's theorem, this means we need 547 chains to cover everything.
I also found it hard to prove that was the largest antichain. Instead, what I did was:
1. It is obvious it is an antichain
2. Come up with a construction which uses that many chains. The trick is to define a NEU map from tiles where
x
+
y
+
z
=
n
to
x
+
y
+
z
=
n
+
1
.
Log in to reply
Yeah, I was thinking of something along that line. Since we have a 547-element antichain, we need at least 547 chains; if we can find a configuration with 547 chains, that gives the upper bound. The only problem is that the construction I found was not very clean and so I opted not to include it.
[This is not a complete solution. There are 2 crucial steps whose proof is not yet provided.]
The main idea is that we're looking at max-flow min-cut repeatedly. The relevant concepts used are dilworth's theorem and hall's marriage theorem .
We approach the general problem of a n × n × n cube. We denote the cubes as lattice points ( x , y , z in Z 3 . We will concern ourselves only with cubes that lie in the n × n × n cube, IE 1 ≤ x ≤ n , 1 ≤ y ≤ n , 1 ≤ z ≤ n .
- Define Π k to be the set of cubes where x + y + z = k , 1 ≤ x ≤ n , 1 ≤ y ≤ n , 1 ≤ z ≤ n .
- A step connects a cube in Π k to a cube in Π k + 1 .
- Interpret the cube as directed acyclic graph . The sets of vertices are cubes in each Π k , and the edges link these cubes from Π k to Π k + 1 .
- An NEU path would be a chain in this graph. We want the minimium number of chains that would cover the graph. By dilworth's theorem , this is equal to the size of the largest antichain in the poset.
- Observe that since the cubes in each Π k are not connected to each other by edges, they form a natural guess.
- Claim: ∣ Π k ∣ is maximum when k = ⌊ 2 3 n + 3 ⌋ , ⌈ 2 3 n + 3 ⌉ . This corresponds to the plane that (most closely) slices through the center of the cube.
- Claim: In fact, ∣ Π k ∣ is strictly increasing from k = 1 to k = ⌊ 2 3 n + 3 ⌋ , and strictly decreasing from k = ⌈ 2 3 n + 3 ⌉ to k = 3 n . Again, think about the planes.
- Now, this only gives us a lower bound for the size of the antichain. We do not know if a larger antichain exists. However, what we can do, is to construct a chain that achieves this bound.
- Claim: Fix k < ⌊ 2 3 n + 3 ⌋ . Consider just the bipartite graph consisting of vertices Π k ∪ Π k + 1 , along with their edges. Then, a perfect matching of this bipartite graph exists. This means that we can find a set of ∣ Π k ∣ edges, which connect a cube in Π k to a distinct cube in Π k + 1 . Note: not all cubes in Π k + 1 are used, since ∣ Π k ∣ < ∣ Π k + 1 ∣ . Hint: We use the theorem that for bipartite graphs, a perfect matching occurs if and only if for all subsets C ⊂ Π k , there are at least ∣ C ∣ vertices in Π k + 1 .
- Similarly, a perfect matching occurs for k > ⌈ 2 3 n + 3 ⌉ , from Π k − 1 to Π k .
- In the event that 2 3 n + 3 is not an integer, then we also have a perfect mathcing from k = ⌊ 2 3 n + 3 ⌋ to k = ⌈ 2 3 n + 3 ⌉ .
- Now, select the perfect matching for each k . This gives us the chain that we desire. It is obvious that each cube is connected to some cube which satisfies x + y + z = ⌊ 2 3 n + 3 ⌋ .
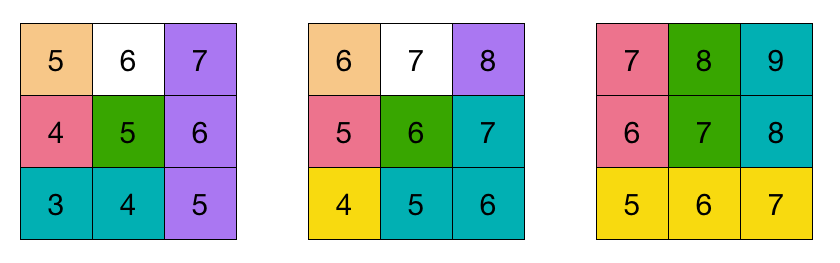
As an example of how this works in n = 3 , here is the layer-by-layer display of the example. The 2 hidden paths are colored in beige and white. The number in each square corresponds to the value of x + y + z . You will see that each colored path has squares in increasing order. The value of ⌊ 2 3 n + 3 ⌋ = 6 , and notice that each square labelled 6 has a different color (meaning they are distinct tiles).
Note: The claims should sound believable/obvious, but they require some work to proof rigorously. The devil is in the details.
For example, the last claim is obvious for
k
<
n
, we we can just "move up". However, it can get tricky when
n
<
k
<
⌊
2
3
n
+
3
⌋
.
The images used in this solution are of a 7 × 7 × 7 cube.
The tiling can be constructed by beginning with a cube partitioned into unit cubes, and by merging the parts together according to some rules.
Observe that a partition T of Z n 3 is a NEU path tiling if and only if both of the following conditions hold for all tiles P ∈ T :
-
No more than one of { p + ( 1 , 0 , 0 ) , p + ( 0 , 1 , 0 ) , p + ( 0 , 0 , 1 ) } is in P for all p ∈ P
-
No more than one of { p + ( − 1 , 0 , 0 ) , p + ( 0 , − 1 , 0 ) , p + ( 0 , 0 , − 1 ) } is in P for all p ∈ P
This is because breaking one of these conditions creates a "splitting" or a "meeting" of paths, and every point in every path has either one or zero points directly "behind", and one or zero points directly "ahead".
Here is an image of all possible mergings between tiles. Notice that the above condition is equivalent to the condition that, according to the coloring of this image,
no two merges of the same color may be adjacent
.

This image more clearly shows the cross-sections of the potential tile mergings.

Now we can find the minimum number of paths by maximizing the number of mergings. The maximum number of mergings is given by the sum of the independence numbers of the graphs constructed by representing potential mergings as vertices, and adjacencies by edges.
It suffices to count the independence numbers of the first half of the graphs, since by symmetry, the last half is isomorphic to the first half (as long as n is odd).
Partitioning each of these graphs into disjoint cliques (pictured as circles in the image) provides an upper bound on the independence number for the graph by way of the pigeonhole principle, and the fact that any two vertices in a clique are always adjacent.
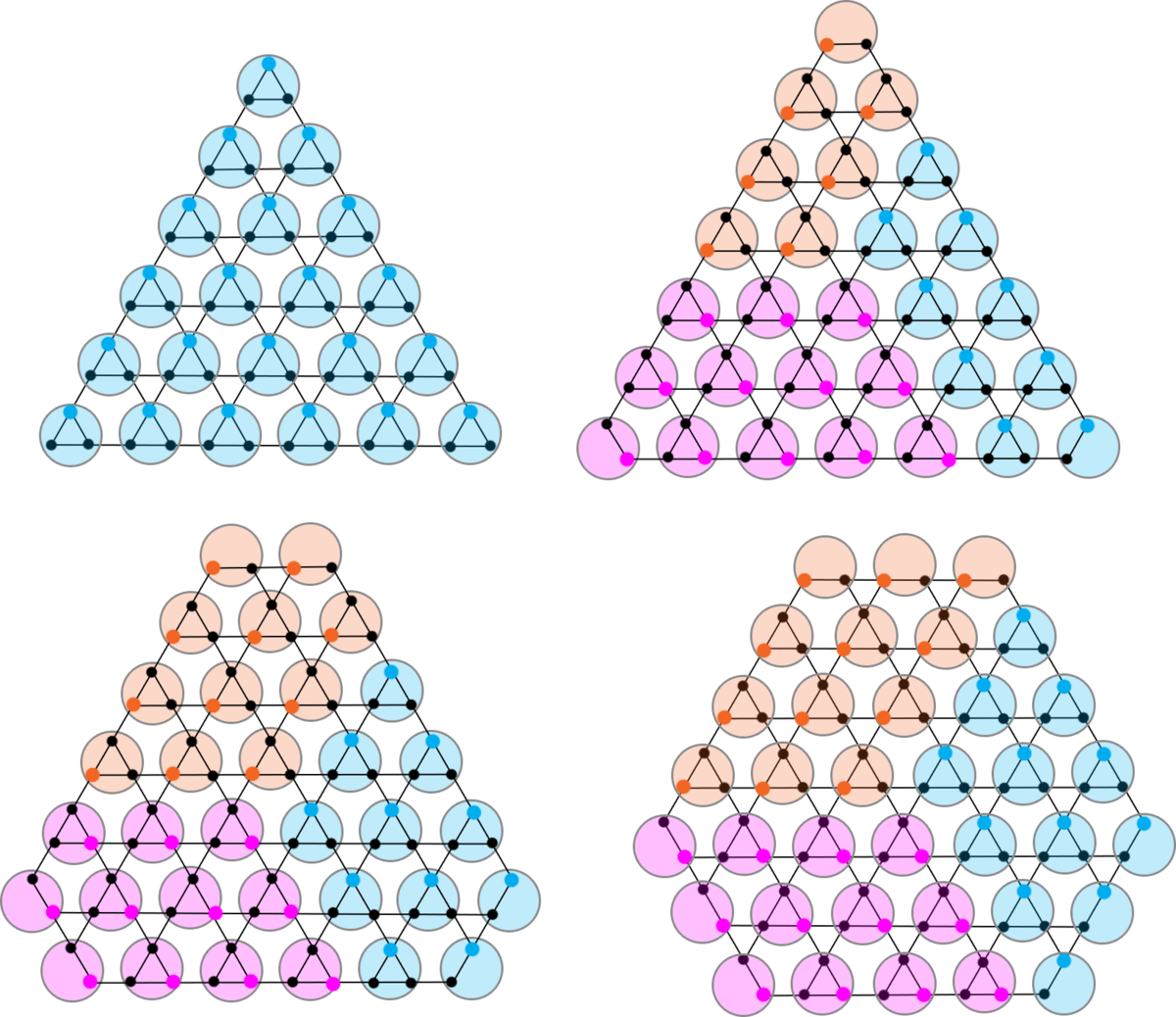
By partitioning the graphs in a manner similar to the image, it is possible to place one vertex in every clique to form an independent set. As such, the independence number is equal to the number of cliques.
For the graphs in a triangular shape, all vertices of the same "type" in each clique form a maximum independent set. For the graphs in a hexagonal shape, the cliques can be divided into three groups, where each group's cliques has a different type of vertex in the maximum independent set. The image shows examples for three different cases.
(Note that this particular partitioning into upward-facing triangles does not work for the other half of the graphs. Instead, they can be partitioned into fewer downward-facing triangles.)
We must now count the number of cliques in each graph. The number of cliques in the triangular graphs are clearly given by the triangular numbers. The number of cliques in the hexagonal graphs can be found by subtracting triangles off of each of the three corners.
Summing it all together:
( 2 2 ) + ( 2 3 ) + ( 2 4 ) + … + ( 2 n ) + ( 2 n + 1 ) …
+ ( ( 2 n + 2 ) − 3 ( 2 2 ) ) + ( ( 2 n + 3 ) − 3 ( 2 3 ) ) + … + ( ( 2 2 3 ( n − 1 ) + 1 ) − 3 ( 2 2 1 ( n − 1 ) ) )
= ⎣ ⎡ i = 0 ∑ 2 3 ( n − 1 ) + 1 ( 2 i ) ⎦ ⎤ − 3 ⎣ ⎡ j = 0 ∑ 2 1 ( n − 1 ) ( 2 j ) ⎦ ⎤
By the hockey-stick identity :
= ( 3 2 3 ( n − 1 ) + 2 ) − 3 ( 3 2 1 ( n − 1 ) + 1 ) = 2 1 n 3 − 8 3 n 2 − 8 1
This is the sum of the independence numbers of half of the graphs.
The number of parts in a NEU path tiling is equal to the total number of tiles minus the number of merges.
Subtracting twice the above expression from n 3 simplifies very nicely:
n 3 − 2 ( 2 1 n 3 − 8 3 n 2 − 8 1 ) = 4 1 ( 3 n 2 + 1 )
This is valid only for odd n . Finally, substituting n = 2 7 grants the final answer.
4 1 ( 3 ∗ 2 7 2 + 1 ) = 5 4 7
I found it hard to understand your question. I think it is better to
- Define a valid NEU tile.
- Define a tiling of the cube with NEU tiles
It is also hard to understand your solution. Adding signposts to indicate what you're achieving would be helpful. E.g.
- Establish a necessary and sufficient condition for a NEU tiling
- Explain what the colors mean (I don't understand this completely)
- Explain what a clique is, and why we're counting that.
Note: Using the ideas that you presented, there is a very simple way to arrive at the bound 547, as the number of integer solutions to x + y + z = 4 2 subject to 1 ≤ x , y , z ≤ 2 7 . It would be great if you can condense the solution to "one-idea". If you're having difficulty, ping me.
You get a lower bound of 547, but for a complete solution, you also need to show that there exists a tiling with 547 tiles. I do not think this is a trivial detail.
Okay this is a really simple solution. (Again.)
I'm not on a computer atm so I need you to visualize this.
I'll give you an example with 5x5x5 grid. There are (1,1,1) through (5,5,5), for comfort.
For your comfort (again), I'll list this so that the ones on a line would be on the same line.
| 1,3,5 | 2,2,5 | 3,1,5 | ||||||
| 1,4,4 | 2,3,4 | 3,2,4 | 4,1,4 | |||||
| 1,5,3 | 2,4,3 | 3,3,3 | 4,2,3 | 5,1,3 | ||||
| 1,4,2 | 2,3,2 | 3,2,2 | 4,1,2 | |||||
| 1,3,1 | 2,2,1 | 3,1,1 |
You see the pattern, right? Then you'll also see that it is not possible for any pairs of given coordinates to be on the same NEU path, thus making the minimum 5+4+3+4+3=19.
You can also see that if you shrink the board to 3x3x3, the minimum gets to 3+2+2=7, satisfying the given condition.
Extend this to 27x27x27, and you see the minimum is 27+(26+25+...+14)×2=547.
See that this is possible by making an L path, (1,k,n) through (28-k,k,n) to (28-k,27,n).
Continue this for k=1~13 and n=1~27. Then there are 13×27=351 paths.
Then there are 14x14x27 grid left. Just fill this with z-axis-parallel lines. 14x14=196 paths.
Therefore, 547=351+196 paths are possible, and so the minimum is 547 .
Question: I was using a similar approach but using 3D paths coming up with an obviously wrong result but would like to know why. Assuming we label the bottom left front corner (1,1,1) and the top right back corner (n,n,n). My paths would go from (1,1,1) to (1,1,n) to (1,n,n) to (n,n,n). The next path would go from (2,1,1) to (2,1,n) to (2,n-1,n) to (n, n-1, n). And so forth. So after n such paths the front side and the right side would be fully covered, leaving a (n-1) x (n-1) x n cube to cover. Rinse and repeat until there is a 2x2xn cube left which is covered with just 4 z-axis paths. This requires n + (n-1) + (n-2) + ... + 4 + 3 paths + the 4 vertical paths. So e.g. For a 5x5x5 cube it would need 5 + 4 + 3 + 4 = 16 which clearly as per above is wrong. Please help me out to see my mistake. Thank you!
Log in to reply
Well, consider this: your pattern applies when the cube is intact, however, when you try to do it with (n-1)x(n-1)xn, you see that it is not possible to make the cube into (n-2)x(n-2)xn using (n-1) paths.
So, the pattern itself is inaccurate, thus leading to a wrong answer.
You can also see that if you shrink the board to 3x3x3, the minimum gets to 3+2+2=7, satisfying the given condition.
Extend this to 27x27x27, and you see the minimum is 27+(26+25+...+14)×2=547.
See that this is possible by making an L path, (1,k,n) through (28-k,k,n) to (28-k,27,n).
Hmmmm, this pattern certainly holds for 3x3x3. But did you literally construct the 27x27x27 thing to work out 547? And how do you know that this is the optimal strategy?
Consider the integer lattice I n = { − n , − n + 1 , . . . , n − 1 , n } 3 . At each stage of a NEU path, the path moves from a vertex ( a , b , c ) to a new vertex ( d , e , f ) where ( d + e + f ) = ( a + b + c ) + 1 .
For any − 3 n ≤ j ≤ 3 n , let S n , j be the number of vertices ( a , b , c ) in I n for which a + b + c = j . No two of the vertices in S n , j can be in the same lattice path, and so any lattice path tiling of S n must contain at least ∣ S n , j ∣ paths.
It is clear that each vertex in S n , 1 can be reached from a vertex in S n , 0 by a valid move, and that every vertex in S n , 2 can be reached from a vertex in S n , 1 by a valid move. Continuing this idea, we can start with the vertices in S n , 0 and develop these into disjoint lattice paths which tile the section of I n for which a + b + c ≥ 0 . We can do the same in the negative direction. Thus we can tile I n with ∣ S n , 0 ∣ disjoint lattice paths. Since we need at least ∣ S n , 0 ∣ lattice paths, the least number of lattice paths that are required to tile I n is ∣ S n , 0 ∣ .
To make this precise, we need to show that, for any 1 ≤ j ≤ 3 n , there is an injection f j from S n , j to S n , j − 1 . This injection is easy to find for n + 1 ≤ j ≤ 3 n , since f j ( a . b . c ) = ( a − 1 , b , c ) ( a , b , c ) ∈ S n , j will do. The case 1 ≤ j ≤ n is more complex, but here is the required injection: f j ( a , b , c ) = ⎩ ⎨ ⎧ ( a − 1 , b , c ) ( a , b , c − 1 ) ( a , b − 1 , c ) b < j , c ≥ j a ≤ − j , c < j o.w. It is perhaps easier to see this injection in action than prove that it is injective. Here is a sequence of diagrams that show the injection f 2 : S 3 , 2 → S 3 , 1 . Each picture shows the array of vertices in I 3 for different values of c . In each level, the vertices belonging to S 3 , 2 are coloured in either green or yellow. Green vertices are ones that will be mapped "horizontally", in that f j will move them to the vertex to which they are attached by a straight line. Yellow vertices are ones that will be mapped "vertically" to the level immediately below (by subtracting 1 from c ). Black vertices are elements of S 3 , 1 which have already been mapped to from an element of S 3 , 2 from a higher level...
Starting at the level c = n and working down to level c = j (inclusive), each element of S n , j is moved one to the left by f j , unless that move is impossible, either because a = − n or because the prospective target vertex has already been filled from the level above. Such vertices are mapped vertically down to the level below. So far, the map is injective.
When this has been completed, there are a total of n + 1 − j vertices in the c = j − 1 level of S n , j − 1 which have already been filled from above. For levels c = j − 1 and on down, the elements of S n , j belonging to these levels lie above the main diagonal of that level.
For the n + 1 − j levels c = j − 1 down to c = 2 j − n − 1 , the elements of S n , j are moved down (in the same level) whenever possible. When such a move is impossible since the prospective target vertex has already been filled from the level above, f j instead maps the vertex vertically down to the level below. The map is still injective.
Below these levels, there will be no vertices of S n , j − 1 which have been filled from above, and so all elements of S n , j can simply be moved down.
If a = 0 , there are 2 n + 1 choices for b for which c exists such that a + b + c = 0 . If a = ± 1 , there are 2 n choices for b for which c exists such that a + b + c = 0 . If a = ± 2 there are 2 n − 1 choices for b for which c exists such that a + b + c = 0 . Carrying on these thoughts, we deduce that ∣ S n , 0 ∣ = ( 2 n + 1 ) + 2 j = 1 ∑ n ( 2 n + 1 − j ) = 3 n 2 + 3 n + 1 As a check with the given data of the problem, ∣ S 1 , 0 ∣ = 7 . We need ∣ S 1 3 , 0 ∣ = 5 4 7 .
I would like to draw attention to @Kevin Lehmann 's comment, in which he demonstrates a simple way to find 3 n 2 + 3 n + 1 NEU lattice paths that tile the cube. This amounts to a considerable simplification.