Cube Path
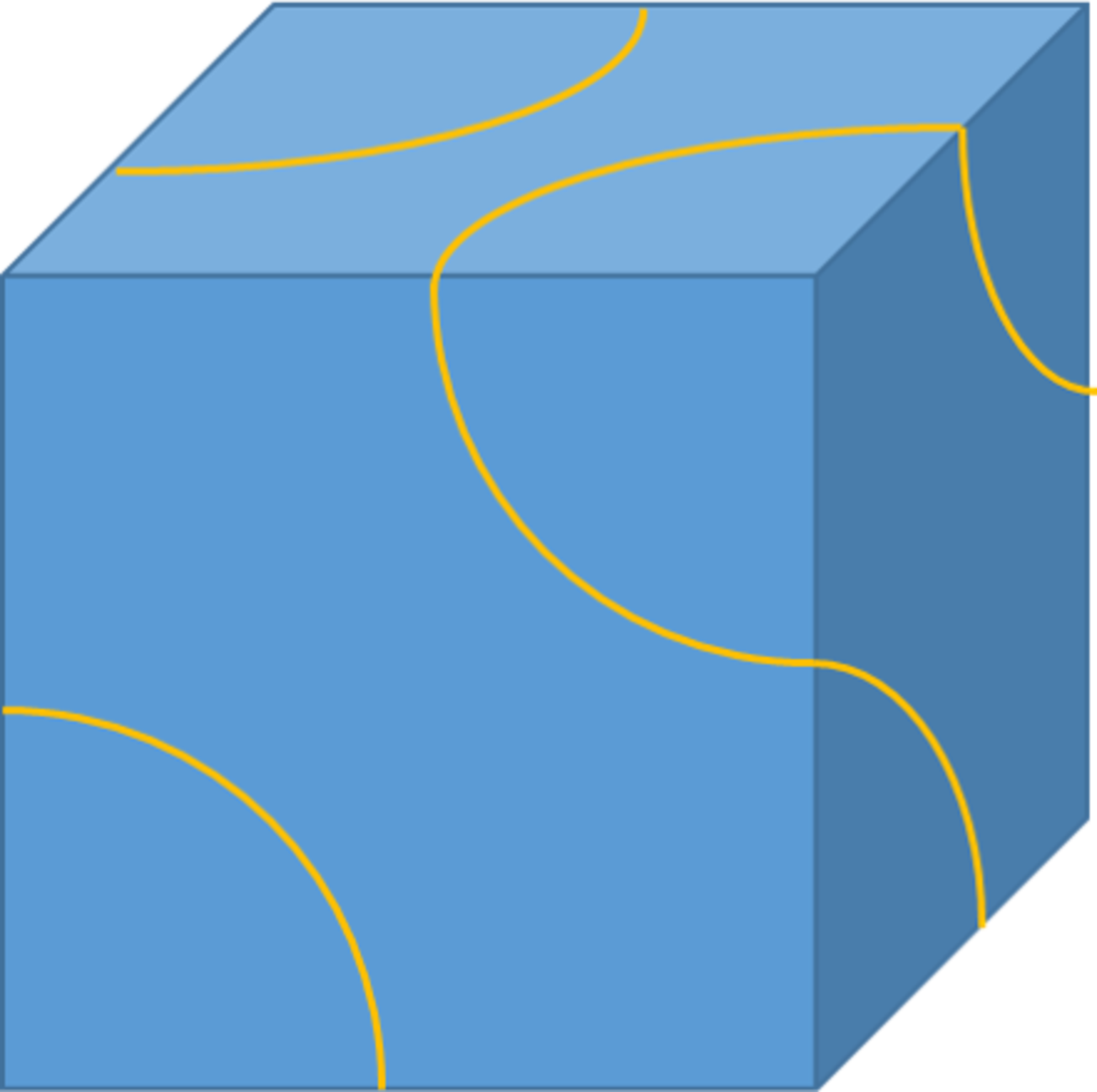
A closed path (one where the start point and end point are connected) is drawn on the surface of a cube so that it crosses each edge exactly once. A path is defined by the order in which it crosses the edges. The path does not cross itself. A partial, potential solution is shown above. A path is unique if the cube cannot be reoriented so that the path is identical to another path.
How many unique paths exist?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is a brute-force method, but it converges quickly.
Since the path cannot cross itself, it must turn left or right on each face. Since it must turn left or right, the path can be defined by a series of left and right turns. We can use a string of 1's and 0's to designate right and left turns, respectively. There are 12 edges, and each time you cross an edge you must turn, so there will be 12 turns to define a path.
Start by generating every possible path. This can be done by representing the numbers 0 through 4095 ((2^12)-1) in binary.
"Rotate" each path to the maximum binary value. Another way to think about this is starting at a different point within the closed loop. In Excel, this can be done with the formula "Left(A1,1) & Right(A1,11)... Left(A1,2)&Right(A1,10)... Left (A1,3)&Right(A1,9)...etc." Where A1 has the 12-digit binary string to be rotated. Then take the maximum value of each rotation. For example, 1 can be represented as 000000000001, or rotated to 100000000000 (equivalent to 2048). 3 can be represented as 000000000011 or rotated to 110000000000 (equivalent to 3072). After rotating each path to its maximum value, 352 unique paths remain.
Any path with three lefts or three rights in a row is a closed path around a cube vertex, and therefore invalid. After this step, 31 paths remain.
Any path containing RLLRLL forms a closed path around 2 vertices. By reflection, RRLRRL is also invalid. After this step, 15 paths remain.
Any path containing LRLRL is invalid because it closes off 4 edges from being able to be crossed. By reflection, any path containing RLRLR is likewise invalid. After this step, 5 paths remain.
These 5 can be evaluated in their entirety to determine that 2 of them are invalid.
Thus, the answer is 3.
Another method is to number the edges and draw a decision tree for every possible next move. Again, since the path cannot cross itself, it must turn left or right after crossing an edge. It cannot go straight across a face. Branches of length 12, that have included every edge are valid.
These are a couple methods I came up with. I am interested to see how others approach the problem.