Cubic Twins
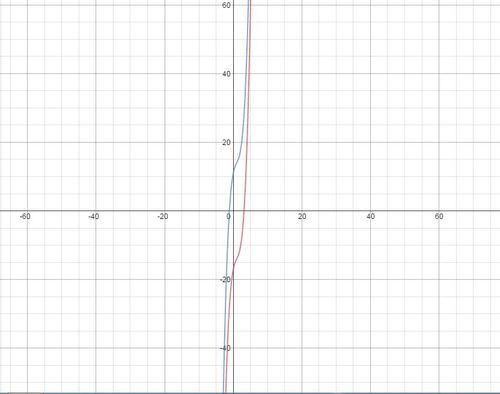 Let
a
and
b
be the only real roots of
f
(
x
)
=
x
3
−
3
x
2
+
5
x
−
1
7
and
g
(
x
)
=
x
3
−
3
x
2
+
5
x
+
1
1
respectively.
Let
a
and
b
be the only real roots of
f
(
x
)
=
x
3
−
3
x
2
+
5
x
−
1
7
and
g
(
x
)
=
x
3
−
3
x
2
+
5
x
+
1
1
respectively.
Evaluate a + b
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
As a side note, you should also state why the second bracket i.e. ( y 2 + z 2 − y x + 2 ) cannot be equal to 0 , otherwise we cannot say that y + z = 0 and a + b = 2 .
Log in to reply
Ishan, thanks for the suggestion. I thought it was unnecessary.
Log in to reply
it should be y^2+z^2>=2yz. its a typo.
Log in to reply
@Chirag Singapore – Thanks a lot. This old man has a lot of typos.
Log in to reply
@Chew-Seong Cheong – could you suggest any theory book for number theory and also one for problems. I have no basic knowledge about it and i dont want to take any coaching for it.
Log in to reply
@Chirag Singapore – Chirag, sorry, I don't know any book. I am also learning. I solved most of the problem cheating with Python programming. I also learn from fellow Brilliant members.
Is there a "wiki" on 'Cardano's method'?If there please give the link.
Log in to reply
There's no wiki as yet. Though you may try to learn from here
I have posted a wiki on Cardano's Formula . Hope it is useful to you.
Log in to reply
Thanks Sir.:)
Sir can you suggest some books for algebra and number theory?
Log in to reply
@Abhi Kumbale – Sorry, I don't read them anymore. So, I can't recommend any.
Hi, there. I greatly enjoyed reading your solution, except I seem to have found a flaw. (Edit: the flaw is minor and easily corrected.) You are assuming y z > − 2 . I tested this in Matlab, and it turns out that y z ≈ − 4 . 5 5 7 7 . By the way, I am working on completing my own solution. I was able to show that 2 is one of the possible values for a + b , but I have not yet proven that it is the sum of the two real roots. You also have a couple of typos where you accidentally put y instead of z . Cheers, James.
Log in to reply
However, the statement y 2 + z 2 − y z + 2 > 0 is still true.
Log in to reply
Just a simple edit using 2 ∣ y z ∣ will do the trick because 2 ∣ y z ∣ − y z > 0 > − 2 .
I didn't realize it before, but it turns out the method I used to get an equation that is satisfied by a + b = 2 very closely resembles yours; except the way you did it was smarter. So, I'm going to try to see if I can do something different for the last part.
Start with: a 3 − 3 a 2 + 5 a − 1 7 = 0 b 3 − 3 b 2 + 5 b + 1 1 = 0 Add the equations above to get: a 3 + b 3 − 3 ( a 2 + b 2 ) + 5 ( a + b ) − 6 = 0 ⇒ a 3 + 3 a b ( a + b ) + b 3 − 3 ( a 2 + 2 a b + b 2 ) + 5 ( a + b ) − 6 − ( 3 a b ( a + b ) + 6 a b ) = 0 ⇒ ( a + b ) 3 − 3 ( a + b ) 2 + 5 ( a + b ) − 6 − 3 a b ( a + b − 2 ) = 0 ⇒ ( a + b − 2 ) ( ( a + b ) 2 − ( a + b ) + 3 − 3 a b ) = 0 But note that ( a + b ) 2 − ( a + b ) + 3 − 3 a b = ( a + b ) 2 − ( a + b ) + 3 − 3 ( ( 2 a + b ) 2 − ( 2 a − b ) 2 ) = 4 1 ( a + b ) 2 − ( a + b ) + 3 + 4 3 ( a − b ) 2 = 4 1 ( a + b − 2 ) 2 + 2 + 4 3 ( a − b ) 2 . If we assume that a and b are real, then this expression is strictly positive. Therefore, if a and b are the real roots of the equation, we must have a + b − 2 = 0 or a + b = 2 . As a bonus, I will show that the complex roots taken in the right pairs also add up to 2 . First of all, we already know by the graph that each cubic has only one real solution. But one can always test by taking the discriminant: b 2 c 2 − 4 a c 3 − 3 b 3 d − 2 7 a 2 d 2 + 1 8 a b c d = − 5 3 2 4 , − 5 3 2 4 . Since it is negative for both cubics, each has exactly one real root. Next, assume x and y are real numbers such that y = 0 , and substitute x + i y into each cubic to set them to zero. I will write them both as one equation for convenience. ( x + i y ) 3 − 3 ( x + i y ) 2 + 5 ( x + i y ) + [ − 1 7 , 1 1 ] = 0 ⇒ x 3 + 3 x 2 i y − 3 x y 2 − y 3 − 3 x 2 − 6 i x y + 3 y 2 + 5 x + 5 i y + [ − 1 7 , 1 1 ] = 0 Both the real and imaginary parts must be zero, so this gives two equations. x 3 − 3 x y 2 − 3 x 2 + 3 y 2 + 5 x + [ − 1 7 , 1 1 ] = 0 y 2 = 3 x 2 − 6 x + 5 Then we can substitute y 2 from the second equation into the first to obtain: 4 x 3 − 1 2 x 2 + 1 4 x + [ 1 , − 1 3 ] = 0 y 2 = 3 x 2 − 6 x + 5 The discriminant of the first equation(s) is equal to -21296 in both cases. So they have only one real root. (Also note that y 2 = 3 x 2 − 6 x + 5 > 0 for any real x . This ensures that the root in question exists as an imaginary root.) The next step is to, similar to the beginning of this solution, consider the pair of equations: 4 u 3 − 1 2 u 2 + 1 4 u + 1 = 0 4 v 3 − 1 2 v 2 + 1 4 v − 1 3 = 0 Add them and then do some manipulations similar to before. 4 ( u 3 + v 3 ) − 1 2 ( u 2 + v 2 ) + 1 4 ( u + v ) − 1 2 = 0 ⇒ 2 ( u 3 + v 3 ) − 6 ( u 2 + v 2 ) + 7 ( u + v ) − 6 = 0 ⇒ 2 ( u + v ) 3 − 6 u v ( u + v ) − 6 ( u + v ) 2 + 1 2 u v + 7 ( u + v ) − 6 = 0 ⇒ 2 ( u + v ) 3 − 6 ( u + v ) 2 + 7 ( u + v ) − 6 − 6 u v ( u + v − 2 ) = 0 ⇒ ( u + v − 2 ) ( 2 ( u + v ) 2 − 2 ( u + v ) + 3 − 6 u v ) = 0 Since 2 ( u + v ) 2 − 2 ( u + v ) + 3 − 6 u v = 2 ( u + v ) 2 − 2 ( u + v ) + 3 − 6 ( ( 2 u + v ) 2 − ( 2 u − v ) 2 ) = 2 1 ( u + v ) 2 − 2 ( u + v ) + 3 + 2 3 ( u − v ) 2 = 2 1 ( u + v − 2 ) 2 + 1 + 2 3 ( u − v ) 2 > 0 , we must have u + v = 2 . This shows that the real parts of the imaginary roots of the two equations add to 2 . Now I will show that the imaginary parts are equal in magnitude. First note that all the roots (and, in particular, the real roots) of the pair of equations 4 u 3 − 1 2 u 2 + 1 4 u + 1 = 0 , 4 v 3 − 1 2 v 2 + 1 4 v − 1 3 = 0 are distinct (this can be seen by substituting a root of one equation into the other and getting a contradiction). In other words u − v = 0 . Therefore, u + v = 2 ⇔ 3 ( u + v ) − 6 = 0 ⇔ 3 ( u + v ) ( u − v ) − 6 ( u − v ) = 0 ⇔ 3 u 2 − 3 v 2 − 6 u + 6 v = 0 ⇔ 3 u 2 − 6 u + 5 = 3 v 2 − 6 v + 5 . Each side of the equation is precisely the square of the imaginary part for each solution. Therefore, they are equal in magnitude. To sum up, the roots can be written in the form { a , u + i y , u − i y } and { b , v + i y , v − i y }, where a + b = 2 and u + v = 2 .
What a great problem!
You don't need Cardano's method. See below.
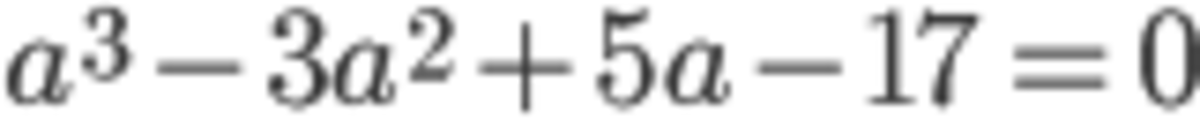
b 3 − 3 b 2 + 5 b + 1 1 = 0
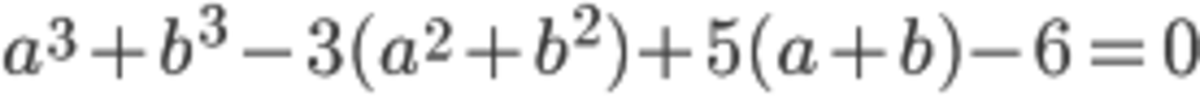
From the above equations we can conclude that a,b are the roots of ,
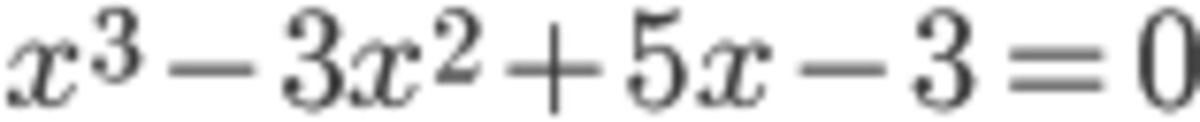
An easy check confirms that 1 is also the root. Hence
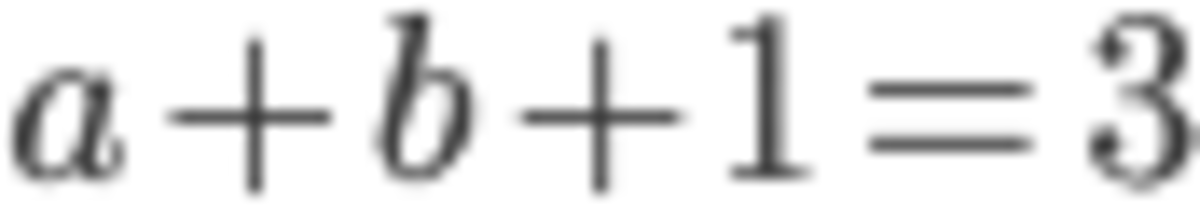
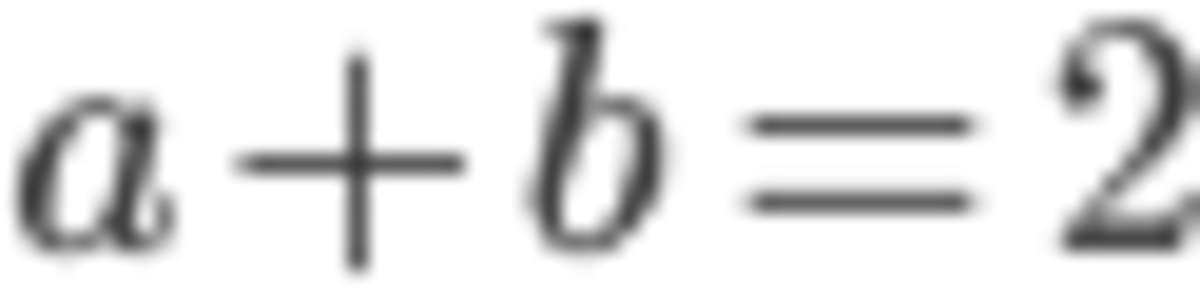
a and b are not the roots of x 3 − 3 x 2 + 5 x − 3 = 0 because, e.g., a 3 − 3 a 2 + 5 a = 1 7 ⇒ a 3 − 3 a 2 + 5 a − 3 = 1 4 = 0 .
Log in to reply
It appears you made the false assumption that a = b .
Using Cardano's method for cubic equation, we substitute:
{ x = y + 1 x = z + 1 ⇒ { f ( y ) = y 3 + 2 y − 1 4 g ( z ) = z 3 + 2 y + 1 4
Since a and b are real roots of f ( x ) and g ( x ) respectively, when:
{ a = y + 1 b = z + 1 ⇒ { y 3 + 2 y = 1 4 z 3 + 2 y = − 1 4
Adding the last two equations together:
y 3 + z 3 + 2 ( y + z ) = 0 ⇒ ( y + z ) ( y 2 + z 2 − y z + 2 ) = 0
We note that y 2 + z 2 is always positive and by AM-GM equality, we know that y 2 + z 2 ≥ 2 y z ⇒ y 2 + z 2 − y z + 2 > 0 .
This means that y + z = 0 ⇒ a − 1 + b − 1 = 0 ⇒ a + b = 2