Block Rolling
A block has edge lengths of 3 cm, 4 cm, and 5 cm (as shown), where opposite faces have the same color. If the block is rolled, which color is most likely to come up on top?
Assume the block's mass is evenly distributed.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
wonderful explanation
Log in to reply
Wonderfully explained! In the example given do you think that there's a way of getting either an approximation or an accurate answer for the probability of each of the 3 colours being on top? Regards, David
Log in to reply
Hi David, finding the probabilities of each side of a cuboid is a tough problem because there are many factors such as how the dice are thrown, the surface on which the dice are thrown, etc. Check this paper for a detailed analysis.
Nicely explained
This helped me review also understand more about energy. Thanks Danielle.
I looked at this from a probability point of view. This makes me wonder if there could be a uniform 3d shape where the closeness of each face to the center of mass is not proportional to its surface area.
I don't agree with the answer. Each color is equally likely.
Log in to reply
Could you explain what part of the solution you don't agree with? or explain why you think each color is equally likely?
Log in to reply
In this problem, we need to do a lot of experiments. This is a probability problem actually not classical mechanics. And the results of these experiments are not exact or accurate. So I think the problem is flawed.
Log in to reply
@A Former Brilliant Member – Yes, this is a probability problem that involves classical mechanics. Finding the exact probabilities of each side is a tough problem, but using logical arguments based on the height of center of mass of the cuboid, one can find out the order of probabilities of each side.
i don't agree with the answer in relation to what was asked and considered. If the question states that the object is not constant technically on its measurement then i would agree to your answer. 1 cm is insignificant on the die size, it is too little to consider, infact if you roll a die with that exact measurement chances are distributed equally and will not give you constant results.
Log in to reply
The green side has almost double the surface area compared to the blue side. This is not insignificant. The measurement chances are definitely not equal.
Log in to reply
it is insignificant, a cm is very small that when it is represented by an actual die can't even noticed the difference. i would agree if it says 4meters x 3meters x 5meters, this is more logical compared to a centimeter. plus there are factors including wind, surface area and the container where the die rolls. :-)
Log in to reply
@Renemar Sultones – What are your thoughts about a die that is 1 mm vs 1 mm vs 1 cm? Here the difference is 0.9 cm.
Very good explanation
Does it not depend on the axis of rotation? If a block is rolled along the axis going through the centre of the smallest rectangle on one side and out the other it's never going to land on a side with the largest area even if that's potentially the most stable.
Log in to reply
Absolutely - The answer to the question is that there is insufficient information on how the block is 'rolled' to give a simple reply.
The word 'rolled' would normally be interpreted (by me anyway!) as being rotated along a single chosen axis of rotation but it might mean something different to the question setter than it does to me!
Log in to reply
Here 'rolled' is used as in 'rolling a die for a board game'. It is thrown randomly on a flat surface.
when you are rolling a die, you are lightly tossing it...so yeah there's rotation along all three axes. The outcome however is pretty random bcoz of the Intermediate axis theorem.
For some reason I thought of a pancake being flipped.
Can we comment on the probabilities of getting different faces?
Log in to reply
Finding the exact probabilities of each side of a cuboid is a tough problem because there are many factors such as how the dice are thrown, the surface on which the dice are thrown, etc. Check this paper for a detailed analysis.
check my answer. Plugged in some numbers.
Imagine it in water - then imagine the block floats. Of course it would never float edge up - only green up is possible. Take away the water and the same hods true
JR
Another problem. A coin lands on either heads or tails. But it could land on "edge". Given the faces as unit circles, what must be the thickness of a coin so that it has equal probability of landing on 1) heads 2) tails 3) edge.
Log in to reply
Nice problem. Finding the exact probability is a hard problem, as one needs to know how the coin is tossed, what surface it is lands, etc. My guess is that if the thickness is of the order of magnitude of the diameter of the circular face, then the probabilities would be roughly the same.
What do you think?
To the original poser: The "block is tossed" would make sense. You cannot "roll" that block as you would a die.
Relevant wiki: Understanding potential energy vs. work
Suppose we have a die with three different side lengths. We know that nature likes to settle into the lowest potential energy state. Having the longest side facing down / up will tend to minimize the gravitational potential energy of the die when sitting on a flat surface. Therefore, we expect the die to settle into that configuration most often, given many trials (throws).
Rotate at 180 degree in any desired direction you'll get requested color.
Log in to reply
Thanks, I got a good chuckle out of that.
Alex, I would advice you to be respectful of other people on Brilliant.
I still do not know what it means to say "roll" a cube. What is really the physical process that is happening?
Log in to reply
I think we're throwing it like we would a die in a board game (like Dungeons and Dragons)
Log in to reply
But isn't Newtonian Mechanics deterministic. What does it mean when we apply probability theory to a deterministic system?
For example, isn't the face that comes up when the die was rolled completely determined by the way it was rolled? Where is the randomness exactly? While resting on the green is the least potential energy state, whether it is a more probable state is dependent on how the rolling happened.
Note that this is different from rolling an usual die, which is a metaphor in probability pedagogy for choosing an element uniformly at random out of 6 elements.
Log in to reply
@Agnishom Chattopadhyay – Yes, it is totally deterministic in principle, on each throw. But we as human beings are not sufficiently aware of our body mechanics to throw the object the same way each time. There is actually a really funny scene in Star Trek - The Next Generation where Data essentially defeats these kinds of table-top games in a casino because he is able to throw the dice to land exactly the way he wants them to each time.
Log in to reply
@Steven Chase – This is interesting. A bayesian philosopher might want to phrase the question in this way, "A die with the given shape is thrown. You do not know any other detail about the throw. What would be the most rational position that you'd believe the die landed in?
Log in to reply
@Agnishom Chattopadhyay – It might also be best to ask for the average behavior over many trials.
@Agnishom Chattopadhyay – Here's the clip
https://www.youtube.com/watch?v=zbkizy-Y3qw
There is an element of randomness to it
Google this: Intermediate axis theorem
This was my first though too. Less mass higher up in the gravitational potential is the most stable state and it would take work to roll away from that state. So, once there, if the rotational energy of the roll is sufficiently dissipated by then it will not leave that state.
Relevant wiki: Understanding potential energy vs. work
Since center of gravity of the block is closer to the green face or its opposed face rather than to other faces. The potential energy will be least resting either on green face or its opposite face. It is a law of physics that systems tend to evolve to minimun potential energy condition.
It doesn't say which way to 'roll' the cube....the answer should be green or blue.
Log in to reply
Think in the other way around, it will take you to same conclusion, the bigger the area of the face the most probability to rest on it. Of course we are assuming the block has uniform density.
By roll, it means throw, not flip over once.
It can be thought of as reasonable that the face with the greatest area and lowest altitude is most likely to settle when rolled. Therefore, the green face.
Unless you specifiy the way of rolling it is possible to turn in anyway and any colour can come
It's true that the center of gravity is lowest if the face with the largest surface area is parallel to the floor (or the axis perpendicular to it is parallel to gravity), but this doesn't help me understand the probabilities. Specifically, note that if the cube is resting on any face, it is a stable configuration, even if it is not in the lowest energy condition. Why would it be more likely to fall into the lowest energy position, vs. one of the local minima represented by the other faces? One reason is as Rafael Barreto suggests, the rate of the dissipation of the energy of the bock, which includes both linear and angular momentum. If that dissipates slowly enough, the block will tend to get stuck in more "global" minima. But if you imagine dropping the block onto a material that absorbed all of its momentum, then it would (in almost all cases) be standing on its corner. To see how this might work, imagine inscribing the block into a sphere. Draw geodesics between the corners. These will partition the sphere into six areas (one corresponding to each side). Imagine dropping the sphere - one of the points on the sphere would touch the ground first. The side of the block corresponding to the area of the (imaginary) sphere would be the side it would end up resting upon, because the center of the sphere/block, which is the center of gravity, will be over that base. The relative areas of the six areas (or 3 pairs of areas) inscribed on the sphere determine the relative probability of falling onto each side. Intuitively the largest side will have the largest area projected onto the sphere.
Logically, Most of the surface area of the cube is green, so green is the correct answer.
Hi, I used probability to figure out the answer.
While the block is spinning is the same thing as if the block was flattened out into a board for throwing darts. And the block falling to the ground is the same thing as a dart hitting the dartboard. The probability of the dart hitting the green space is the largest. Thus the answer is green.
When the question states "the block's mass is evenly distributed", it means that "randomness applies". The probability is then linked to the surface of each face. Blue area is (3x4=12). Red area is (3x5=15). Green area is (4x5=20). So P(Green) > P(Red) > P(Blue).
As the mass is evenly distributed the is no need of loaded die concept, assuming it as a fair die, all the side have an equal chance of coming on top. But as the dimension are different the outcomes when the die is rolled are affected, as the green side is the largest the die is most stable there and the chance of the side opposite to it which is also green are much higher
Yes, a formal way to see that the green side is more stable is to see that when balanced on this side, the center of gravity is at it's lowest point.
But, it doesn't say how many times do we have to roll the block and in which direction (I sure am wrong, just want to know where is my mistake).
It was green because it has a bigger space than blue and red. Therefore, the answer is green.
Let's say probability is proportional to the area.
Now P(green)~(4x5)=20
P(blue)~(3x4)=12
P(red)~(3x5)=15
add them up: 20+12+15=47
So P(green)=20/47 | P(blue)=12/47 | P(red)=15/47
Probability of landing a color is 1/3
So the final probability becomes:(multiply 1/3 with the previously found fractions)
So P(green)=20/141 | P(blue)=12/141 | P(red)=15/141
........therefore landing a green face up is the most likely event!
Why did i choose area? you'll see that greater is the area, the lower is the Center Of Mass of the body. Since having the green face down means the COM will be at the lowest possible point(lowest potential energy), it is most likely to end up in that state if you try to try to put it in an unstable state by tossing it.
There is more surface area on the green side, so the opposite side is also green.
Simply, green face have largest surface area, so it is most likely to come on top
Both the left and right sides have the colour green so wherher it is turned clockwise or counterclockwise you have the colour green ontop and since it is the heavier side it comes up
The problem is flawed
At first I thought "this problem is flawed.... It does not specify that the block's energy dissipates". But then I realized "if the block's kinetic energy does not dissipate, it will never stop rolling", which is a premise.
So, since the block's energy dissipates, it means the entropy of the universe is increasing (we know this is an irreversible phenomena), and this is the only reason that the "principle" of minimum energy applies to the block's mechanical energy.
Note that the universe's total energy is always constant.
By the way, it is a common misconception thinking on this minimum energy "principle" detached from entropy and temperature (especially the second law). This is the reason why so much people has issues to understand the meaning of the thermodynamic potentials (the "free" energies).
On the other side, one must note that if the kinectic energy dissipates fast enough, it will stop at the first face that touches the floor (in a local minimum of the potential energy). And, since the problem does not specify the energy rate dissipation, this problem is flawed.
Joking.... We physicists do not care for so much for the details, and this is the reason I miss the majority of the mathematical problems of this platform.
I did not really get your point.
This is easier to understand if we think of a more extreme example. Suppose that we have a block that is 2 cm by 5 cm by 10 cm: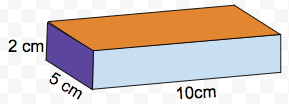
Any of the three colored sides can come up on top:
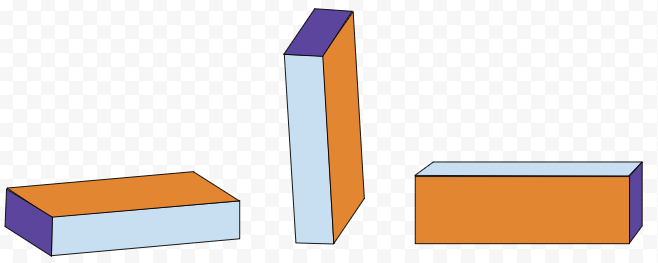However, we would expect the first case, when orange side is on top, to occur most often. The simple explanation is that this is the 'most stable' configuration. But why? Since the block is uniform in mass, the center of mass is closest to the ground when the side with the greatest surface area is on the bottom. When the center of mass is closer to the ground, the block is in a lower potential energy state. Therefore, when an orange side is facing up the block will be at the lowest potential energy.
When the block hits the ground, it will be spinning. As this energy dissipates, the rolling slows until the block is about to settle. If the block is currently on a side where the center of mass is high, then it won’t take a lot of torque to tumble the block over (onto a different side). If the center of mass is low, it will require a very large torque to tumble. The orange side, with the lowest center of mass will be able to capture the most “blocks about to settle down.”
This holds true for the original block. When the green side is facing up, its matching side on the bottom has the greatest surface area. Therefore, the center of mass will be closest to the ground in this case.