Curious Chess Composition

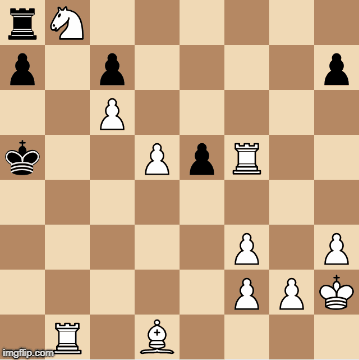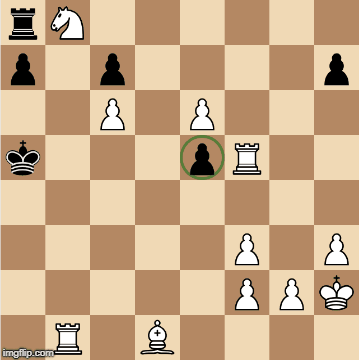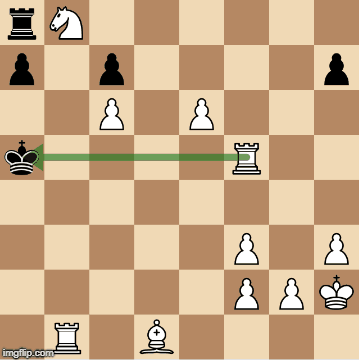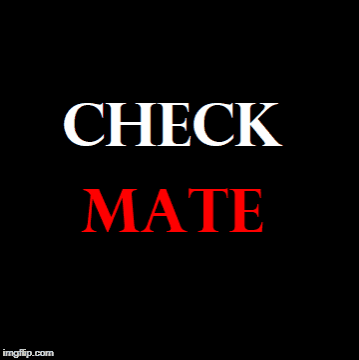
Move the pawn from d5 to e6 (en passent), an instant checkmate. This is because the only possible previous move for black is pawn e7 to e5 (as pointed out by the author, since the computer plays optimally, the pawn would have not been on e6 or else it would take the white rook on f5 instead), thus making the en passent move possible.

"On your last move, you captured the black queen with your king on h2, to complete a trade of queens.":

This line is important as it shows that the last move that you, as white, made didn't put black in check . However, since black must have moved a piece between white's last move and the current state of the board (as it is currently white's turn), we can work out what black's move was.

• Black can't have moved one of the pawns on the 7th rank, as that is the starting position of pawns
• Black can't have moved its rook since it can't have moved from anywhere to square a8
• Black can't have moved its king since all the squares surrounding it are protected by white. Also, the king can't have moved to a5, out of check, since we know that white didn't deliver check on the last move

This means that on black's last move, the pawn on the e-file was moved.

---

Black's last move involved the pawn on the e-file:

Now the pawn on e5 could have come from one of two squares, either e6 or e7. If the pawn was on e6, the optimal move for black would have been to capture the rook on f5, rather than playing e5 as this would delay the checkmate. Note that the checkmate would still occur, since white (being careful to avoid stalemates) could promote a pawn while black's king and rook are helpless. Since the white rook is clearly still on the board, the black pawn didn't come from e6.

This means that black's last move came from e7.

---

Black's last move was moving the pawn from e7 to e5:

Finally, since the black pawn moved two spaces, the white pawn on d5 can capture via "en passant", delivering checkmate in 1 move, as shown below in the animation. Since 1 move is possible, and wouldn't be possible without the white rook, this is why, earlier on, black would've captured it if given the chance to.

---

As an aside:

If en passant wasn't to be used, the best route to checkmate for white would be for the rook to capture the pawn on e5. Black would attempt to extend the game by capturing on b7 with the rook, to which white would recapture on b7 with the white rook from b1. Then, none of blacks moves would make any matter, as the other white rook could manoeuvre from e5 to e3 to a3 to deliver checkmate in 4 moves.