Current Sink
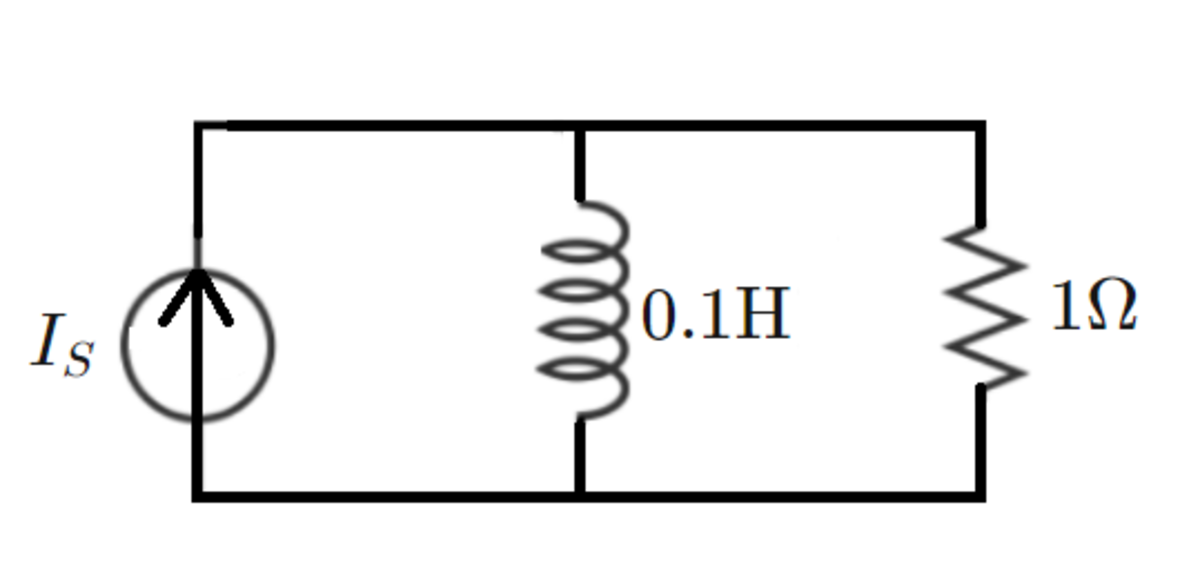
A current source injects into an R L network as shown. The injected current is defined as follows (it is a half-wave rectified sine):
y ( t ) = 5 sin ( ω t ) I S = y ( t ) if y ( t ) ≥ 0 I S = 0 if y ( t ) < 0 ω = 1 2 0 π
At time t = 0 , the inductor has no current flowing through it. Let I R be the current through the resistor.
What is the magnitude of the I R current peak which occurs between t = 0 . 1 5 and t = 0 . 1 6 ?
The answer is 3.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I initially attempted an analytical solution but realised soon that solving the definite integral involving a piecewise continuous function is an uphill task. Also, the final answer I obtained is slightly different than yours.
Log in to reply
Everything looks the same as what I have, except for the interval in which you are checking for the peak. Given your interval, it will naturally be a smaller peak than the one between 0.15 and 0.16.
Log in to reply
Oh, I misread the question. Coded the interval wrong. I got lucky!
Fixed the solution.
I think it is interesting that we see this kind of behavior, even without magnetic saturation of an iron core.
Log in to reply
Well, I see that the inductor builds up energy, as expected. I am unable to latch on to the interesting behaviour at the moment. You could tell me what you see.
Log in to reply
@Karan Chatrath – This is actually the equivalent circuit for a current transformer. Current transformers are typically used to create a proportional replica of the current flowing through some primary apparatus. The current I S is this replica current. The current flowing through the resistor is called the "burden" current, and it is accessible to a measurement device. Ordinarily, the magnetizing reactance (modeled by the inductor) is quite large relative to the burden resistance, so the burden current closely follows the replica current. But if the magnetic core saturates, a considerable amount of the replica current shunts into the magnetizing branch, distorting the measurement. Here, we see a sort of distortion even though no iron effects are modeled.
Log in to reply
@Steven Chase – Thanks for the explanation. I can appreciate what is said, however, I do not fully understand the concept behind the current distortion. I will read a bit more and share thoughts if I have any.
Log in to reply
@Karan Chatrath – By the way, how would you solve this analytically? It seems Alak tried it that way
Log in to reply
@Steven Chase – I have posted my attempt and verified my result using a computer.
Log in to reply
@Karan Chatrath – That's pretty impressive, thanks. I assume this yields the same answer as the numerical approach.
Log in to reply
@Steven Chase – Yes, I get an answer of 3.7339. Samilar as numerical. Like I said in the first comment, solving definite integrals involving piecewise continuous functions is cumbersome. That's why I went the numerical route initially.
Solving the problem analytically, I get the peak current as 4.968, much higher than the answer.
Oh, I thought the peak which is sought after is the one which occurs at semiperiod, not the maximum in the given period..
That aside, I must point out that your semi-analytical approach neglects the current dynamics during the period when the source injects zero current. During this period, differential equation governing the circuit becomes homogeneous and the magnitude of the currents through both, inductor and resistor, decrease exponentially (which can be seen on your plot). However, at higher frequencies, or generally when ω L / R → ∞ , this exponential decrease is very slow and thus almost negligible and that's why your analytical approach maybe led to pretty accurate result. At lower frequencies, decrease is be much more rapid and thus has to be accounted. When the source starts again injecting, a sharp peak will occur in the resistor current. That's the peak I thought I should look for.
Log in to reply
Yes, you have made a good observation. I have not considered the homogenous equation itself. When I can, I will revisit (possibly re-attempt) my working and comment further.
Semi-analytical solution:
Consider the differential equation governing the current flow through the inductor:
d t d I = 1 0 ( I S − I )
This implies:
d t d I + 1 0 I = 1 0 I S
d t d ( e 1 0 t I ) = 1 0 e 1 0 t I S
d ( e 1 0 t I ) = 1 0 e 1 0 t I S d t
When t = 0 then I = 0 . Then:
e 1 0 t I = ∫ 0 t 1 0 e 1 0 t I S d t
Solving this monster on the right-hand side is very tedious. Here is my attempt.
It so happens that: t = 0 . 1 5 = ω 1 8 π
Let p = ω π
The integral on the right-hand side can be written as:
e 1 0 t I = ∫ 0 p f ( s ) d s + ∫ 2 p 3 p f ( s ) d s + + ∫ 4 p 5 p f ( s ) d s + + ∫ 6 p 7 p f ( s ) d s + ⋯ + ∫ 1 6 p 1 7 p f ( s ) d s + ∫ 1 8 p t f ( s ) d s
Where f ( s ) = 5 0 e 1 0 s sin ( ω s ) . In the integral above, t > = 0 . 1 5 .
Let:
S = ∫ 0 p f ( s ) d s + ∫ 2 p 3 p f ( s ) d s + + ∫ 4 p 5 p f ( s ) d s + + ∫ 6 p 7 p f ( s ) d s + ⋯ + ∫ 1 6 p 1 7 p f ( s ) d s
Then:
e 1 0 t I = S + ∫ 1 8 p t f ( s ) d s
The current through the inductor is:
I = e − 1 0 t ( S + ∫ 1 8 p t f ( s ) d s )
Solving for S was done using a Wolfram Alpha like tool. The integrals are very doable but too cumbersome.
Finally:
I R = I S − e − 1 0 t ( S + ∫ 1 8 p t f ( s ) d s )
I R is a function of t such that t ≥ 0 . 1 5 .
From here, one can take a more analytical approach of finding local maxima by differentiating with respect to t , equating it to zero, and searching for the solution that lies between t = 0 . 1 5 and t = 0 . 1 6 . I have not done this. Instead, I have just plotted this time function within the specified interval and extracted the maxima.
So its not entirely analytical. I have made use of a computational tool at the end.
Numerical Approach:
Governing equations of the circuit are:
d t d I L = 1 0 ( I S − I L ) I S = I R + I L I L ( 0 ) = 0
The following plot illustrates the current response of the circuit:
Simulation code is as follows: