Cushion Shot in Billiards
Suppose we aim the cue ball at the cushion with some angle of incidence θ i = 9 0 ∘ . How will θ i compare to θ r , the angle of reflection?
Naively it may seem that we can apply the law of reflection (that the angle of incidence is equal to the angle of reflection), but in practice we can't since some energy is lost upon colliding with the wall.
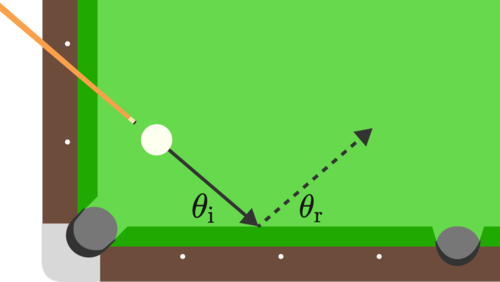
Details and Assumptions:
- For simplicity, take the cue ball to be a point particle that has no sliding friction with the wall.
- The ball doesn't curve or jump on its way to the wall.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Is this all actually true in reality? From experience on pool tables I know that if you bounce the ball hard back and forth across the table, the angle of incidence increases (ie: it tends towards 90 degrees). This has been known to cause grief when attempting to get out of particularly awkward snookers. Since this is something that actually happens, it would appear the theory above is incorrect in actual practice, at least in some circumstances.
Log in to reply
I do not agree with the statement that there is no force in the x direction, since the friction will also contribute to the reaction force, and the relation between the angles will depend on the relation between these effects.
Log in to reply
Totally agree. I thought the same.
I'd add that, even though the ball is hit centrally, it will receive angular momentum by hitting the wall. This, I believe, leads to an opposite effect, i.e. the ball will run towards the perpendicular.
Log in to reply
@Phil Rodeo – My initial intuition said the spin the ball gets would intensify the effect, so the resulting angle would be even smaller. I'm not really good at pool, but as far as I remember, the angle starts to increase only at the second reflection (and that FEELS OK for me, considering the direction of the spin). It would be interesting to see an explanation for this, I tried but I'm not sure about it. Anyone, please? :)
Log in to reply
@Laszlo Kocsis – Yeah, I think this is one of those cases where the answer depends on the level of detail. I think the most reasonable answer is that the angle will remain the same (more or less) but the velocity will be lower.
In reality, I also agree that the angle of reflection increases, which I believe is to do with the way the cushion compresses and expands during the collision. In this case, while this answer may be fine in theory, it doesn't match up to reality.
I would argue that this effect of the cushion absorbing some energy from the y component, while accurate, is not the most significant factor in determining the path of the ball leaving the cushion.
Log in to reply
I agree that in reality the angle of reflection increases especially as the force behind the cue ball increases. I'm not sure why but I think it has to do with the the shape of cushion deformation (absorbing energy) of the cushion rubber and speed of cushion recoil (releasing energy).
Log in to reply
@Jeff Hunt – billiard pool problems cannot assume no friction, as friction is almost the most important thing that makes into the play. The friction is controlled with the tissue material that covers the whole pool and this makes the player to not to have to wait until the energy loss stops the play. The other things, the rubber quality (to make the hits the most elastic), the pool mass (to absorb all the linear momentum from the balls and return it completely) are made to make the play the most ballistic possible.
Indeed, the cushion compresses being inelastic, makes the ball to lose Vy and decrease the angle. In an extreme inelastic case (suppose the rail made of some viscose gel) the result is the ball rolling along the rail, with no rebound. The real increase of angle comes from the rotation energy that transforms in angular momentum, that comes from the friction between the cushion and the ball surface, that induces an amount of angular moment to the ball and makes it emerge rotating along the vertical axis (but the problem assumed no friction at all, as if the cushion were made of ice). As the friction is static (no slip) no energy loss is produced by this. If the ball slips somewhat on the wall (this is controlled by the nature of the tissue that covers the whole billiard pool) only part of the rotation (anti-rotation or no rotation at all) is traduced to angular momentum and makes the Vx to reduce more or less. Also, the rubber quality of the rail makes the Vy to decrease some amount (also some energy is passed to the pool and makes the Vy to be smaller, but this energy loss is almost null, the better the rubber, the more elastic hits are observed)
I agree. This is why I gave the 'incorrect' (first) answer.
Log in to reply
I gave a "it is inconclusive" response. The problem says no friction, but playing billiard with no friction is like playing to break subatomic particles... what is the energy sink in case no friction is considered.
I think in reality, the angle can get bigger or smaller. If you hit the wall close to normal, most of the effect is obviously on the normal velocity. If you hit the cushion at a shallow angle, there's less deformation of the cushion (keeping its response more linear) but you can get more significant effects with sliding friction (giving it a spin etc).
Log in to reply
Indeed, you are able to control it with the side effect you give to the ball. The limit comes with the friction limit that makes the ball to slip once passed the static friction limit.
Yes, but you introduce a new problem.... when you do the first hit, the ball has no angular momentum on the Z axis, and the angle makes it gain some momentum on the Z (or -Z) direction. When it hits to the opposite rail, it has a counter effect due to the first hit, that makes the loss of momentum more significative (this is not in the original problem) so the gain of reflection angle (towared 90<) is greater than in the original problem. This continues to work and make the reboundings to oscillate between to points. That is the same effect as if you let a ball to rebind against the floor with some backwards effect, it will be rebounding between two points, as the ball momentum compensates between each two rebounds in the floor.
David's answer is correct. The given answer to the question is just flat wrong. The question was obviously posed and answered by a non-player. The angle of reflection is often greater (closer to 90°) and becomes significantly greater as more force is applied. It has to do with the rebounding cushion wanting to throw the ball directly across the table. This effect is well know by pool players and is routinely used to alter the reflected path of the ball to a desired direction. The harder the ball is hit the more you "shorten" the angle. Any decent player knows this and uses it routinely.
What about decrease in horizontal component of velocity because of friction force acting between table and ball .
In the friction free case, yes, the only force is in the y direction and that simply changes the direction of motion to -y. However, when friction is involved, the ball starts to rotate around the z axis due to the frictional force exerted in x direction. The energy of the spin reduces the x velocity component. However the acceleration in the y direction is significantly larger than any effect in the x direction for most angles, and hence will likely experience significant degradation if the material on the pool table absorbs the energy as the incoming ball collides. So my guess is that the y component will be more dramatically affected and hence the angle of reflection will be less than the angle of incidence.
Log in to reply
two things... why do you speak of acceleration in the y direction... in the case of a perfect (or quasy perfect) elastic hit, the velocity on the Y axis will be -Y prior to the hit (to conserve linear momentum law) so we have Vx' < Vx and Vy' = -Vy, and finally we have larger reflection angle. On the other side... you have some energy loss due to the inelastic of the rail, you get |Vy'| < |Vy|, so this makes the reflection angle to be less than the incidence...
Your answer is not strictly true. The ball can lose energy in the x direction due to friction between the ball and the cushion.
Log in to reply
I agree, but I would argue that the magnitude of the wasted energy in the x direction is small compared to the y direction, so the angle is still less after the collision
That's why we state the assumption that there is no sliding friction.
right answer but incomplete/incorrect explanation. the rail is not a perfectly rigid object. hence there is deformation. that deformation allows for the x-component to change
Log in to reply
a ball with null effect will gain some angular momentum due to the friction with the rail, this makes the reflection angle to be greater. Billiard tables are made so the rails try to make minimum energy loss in hits, and friction is somewhat controlled by the nature of the tissue that covers all.
The answer is incorrect because the question makes an untrue assumption that there is no sliding friction. In other words there is no Y force component only an X component and therefore the ball would bounce at 90* off the rail.
Log in to reply
Hey Ed, I agree that the full reality of a cueball colliding with the cushion is more complicated than this problem is. I've updated the wording to make the assumptions more clear.
Log in to reply
You make the incorrect assumption that the ball has no friction in the parallel direction to the side.... but you assume also that the ball is losing energy in the billiard play. What is the origin of such an energy loss? Which assumption should be valid? With such an amount of false premises, what should we conclude? You have included a response (not concluyent) and mark it as false response.... what can be deducted as true when the premises are false? The origin of the difference between the incident/reflected angle comes mainly from the rotation of the ball along the vertical axis, and this makes it possible (I've done that) to make the reflection angle to be larger or smaller than the incidence angle. And this comes from the friction along the parallel axis. Should the ball being radius R hit the wall, the only way that the friction to the wall doesn't influence in the X direction component is that it is rolling at \omega = Vx / R. This is one reason that if you don't give effect makes the ball to get a greater angle when rebounding to the edge. If you assume there's some energy loss in the hit to the wall, the reflection angle (as shown in the graph) should be less, because of the loss of linear momentum with the hit. So we have two assumptions going in opposite directions, both are due to the friction to the wall, this is the main fact.
Log in to reply
You make the incorrect assumption that the ball has no friction in the parallel direction to the side.... but you assume also that the ball is losing energy in the billiard play. What is the origin of such an energy loss? Which assumption should be valid?
I don't agree that the two assumptions (no sliding friction, and inelastic collision) are at odds. If the collision is inelastic when the ball hits the wall, then the wall dissipates some energy in compression. Without sliding friction, the movement along the wall maintains its momentum.
Keep in mind, I'm just talking about the simple problem outlined by the assumptions (where μ k is zero).
According to Newton's second law at the very moment of the collision with the wall the reaction force Y component is exactly the same but opposite. Therefore the initial angle of reflexion will be exactly equal to the incidence angle. Right after that distance the rolling friction could affect the direction of the ball. If you are going to consider real situations you have to include ALL posible physical effects on the ball and not only part of them.
What does Oi and Or mean it never explained that
Log in to reply
They are the angles that the path of the ball make with the wall, as shown in the diagram.
It might be interesting to add that in practice, the angle often INCREASES after hitting more then one wall. I would say that this is because of the sideways spin the ball takes on after hitting a wall (there IS friction after all...).
In practice, with no english applied to the ball, its angle of reflection increases with each reflection. Ask any billiard player. I have long wondered about this, but as yet, have never received an explanation.
Log in to reply
It would seem to be because of the spin on the ball. Even when you aren't applying english, the ball of course has a lot of top spin. The spin of the ball then has to change directions after hitting the wall. Perhaps for a mathematical explanation you can look at angular momentum.
Log in to reply
Even if you don't left/right spin the ball, you can change the angle that the object ball comes off the rail by modulating the speed of the ball. The harder the object ball hits the rail the more you increase theta r . If you hit it hard enough, you can even make theta r >90 (the ball seemingly magically comes right back at you... even if there's no left/right spin). This has to do with rail deformation (compression).
When the cue ball hits the cushion, the cushion "grabs" the ball for a short instance of time it releases it with some spin This creates angular momenta perpendicular to the table. This spin must be created by slowing the ball in the direction of travel parallel to the cushion - and therefore increases the angle of reflection.
It seems to me that none of those who have commented on the answer to the problem have played either snooker,, billiards or pool! To all intents and purposes the angles are definitely more or less equal !! Effects of spin, friction, energy loss are negligible otherwise playing the game would become exceedingly complicated. Too much theory and not enough practicality methinks.
Log in to reply
If you put sufficient spin on to the cue ball, you can make the angle greater or smaller
Log in to reply
and also, if you shot your ball (without effect) against the rail (normal 90º shot) you'll see the ball jumping on the air because the rolling effect of the ball that induces a vertical force that makes it jump over the table.
Being an avid pool player, I can assure you that the angle actually increases. The more force placed on the ball from the cue, the more the angle increases. The reason for this has to do with what happens the moment the ball's direction is reversed by the cushion. At that moment, the compression of the cushion is not uniform. It is more compressed in front of the cue ball and less compressed behind the cue ball. As the cushion decompresses, some forward velocity is lost, causing the angle to increase. Has nothing to do with friction, which the problem was careful to set at 0 in the assumptions. In reality, the friction from the cushion imparts a slight outside spin on the cue ball while also increasing the angle.
Log in to reply
Nope, if you give some amount of side effect to make the ball some spin in the vertical direction (to make is roll as fast as it moves aside the rail) it should make a rebound with the same angle as the incidence. But if you give it no side effect, the ball with hit laterally against the wall and receive some momentum, that makes the velocity along the rail direction to get larger (or dismiss, if you give some forward effect) if you throw the ball to make rebounds along the three 90º sides (a tie shot) you'll see that the routes are parallel at each two rebounds.... this is because after the first rebound, the ball has a positive angular momentum that conserves the angle as in a ballistic problem (punctual particles instead of balls)
This question was confusing to me. As a player, I've seen the ball tend to increase in angle. I think this question would have been better if it were air hockey pucks and soft cushions, not billiard balls. The problem is there is spin on the ball as it rolls. Somehow this spin and the friction with the wall causes the angle to increase, not decrease.
I can't tell you exactly the formula for this. But, if you consider forward momentum moving from left to right, in the diagram, and if you understand that this is the over-riding force, in play, and if you understand, that the ball will rebound with decreased energy, as a result of the cushioning, of the felt, it is easy to see the ball balancing the energy bleed, to the narrower rebound angle as the rebounding force was not equal to the impacting force, and therefore, the resultant angle is the result of the force of forward momentum affected by the decreased rebound energy.
Every snooker player knows this. It is called the coefficient of restitution. The ball comes off at a lesser angle. UNLESS you put spin on the ball. Counter clockwise it will rebound at at a greater angle, clockwise, a lesser angle.
This is more a comment than solution. First, as a pool player I cringe when I see the cushion referred to as a "wall". That's just plain wrong! "Wall" implies a static surface with no effect on the outcome while in fact the cushion is an active part of the physical equation. Trying to eliminate all of the variables in the action would reduce it to being the same as reflecting light and the angle of reflection would equal the angle of incidence. Practically speaking there are so many forces at play here it would difficult to address them all in solving the question. There is the friction factor of each surface, the ball, the tablecloth, the cushion. There is the speed/force of the cue ball hitting the rail which changes the recoil of the ball from the cushion and the gripping (friction) of the cloth on the cushion. There is the "liveliness" of the cushion rubber itself. Somehow a competent pool player can absorb all these factors and more and adjust accordingly for the desired result.
Right on, Jeff. The best pool players ('the pros') have an intuitive sense of the way the cue ball (and the balls being struck) will react upon hitting the rail, which leaves all the 'rigorous' analyses in its wake. Let the mathematicians take up the sport in earnest and see how soon they will abandon their formulas and develop their intuitive 'feel' (married to their visual responses) to master this exciting pastime.
I also cringed a little at the term 'wall'. There are also no assumptions made about the rails. This means that all answers are correct based on how the compression of the rail, which is in turn dependent on the current environmental conditions (heat, humidity, pollutants in the air i.e. smoke, etc.), affects the angle. As it compresses it cradles the cue ball and changes the angle of the surface it is ultimately being released from.
This is why kicking off of two or more rails is always easier than just one. All of these factors are reversed on the next rail due to the acquisition of spin. That said kicking is still an art, or magic trick if your first name is Efren.
I wrote about bouncing ball physics years ago, to explain how I made a bouncing ball program in Javascript (http://marcobrandizi.info/static/balls/balls.html).
I think the easiest way to answer this problem is to break it down to something we understand better...Light!
As stated in the problem the ball would obviously lose some kinetic energy. Now imagine if this was light traveling. Let's assume that the light is arriving from a point that is found by extending the path of reflection (as shown in the image) backward.
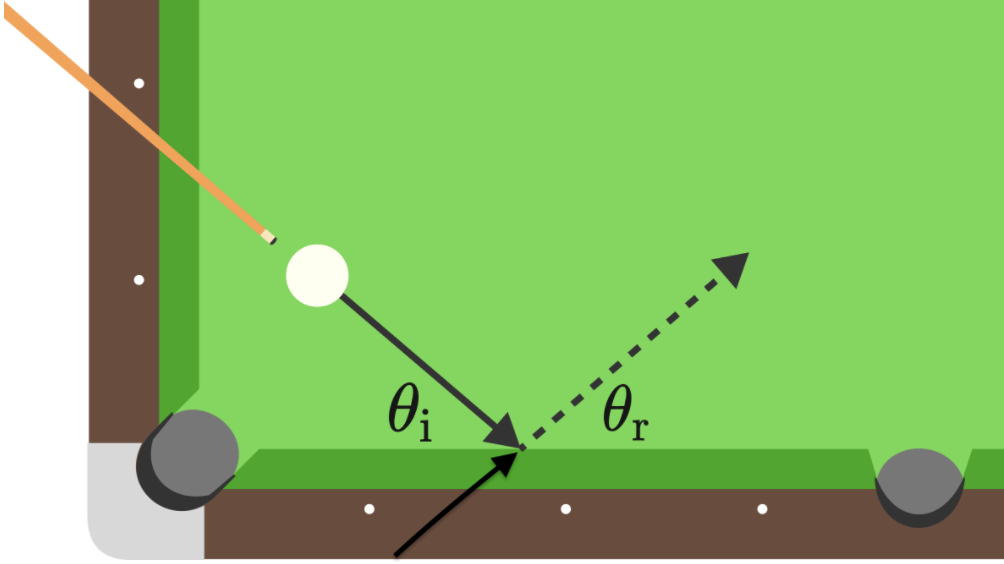
Now if one were to imagine that the light is changing to a medium in which it travels slower, one could reason that the angle of incidence is always greater than the angle of refraction.
Since the spin could be in either direction the average response is nullified and i don't think it even matters with a point mass. No sliding friction, odd phrase, but that means the ball is stationary at the point of impact.
The only factor (thing) I could imagine affecting the angle of reflection was the reaction force from the cushion, which is softer than the cue ball. The cue ball loses energy initially, we could say it is transferred to the cushion, and then back to the cue ball. Increased amount of energy away from (/perpendicular to) the wall, consistent energy parallel with the wall.
In my eyes this means the angle increases after collision.
The angle of reflection is lesser in value to the angle of angle of incidence because as per the question some energy is definitely lost when the ball collides with the wall and hence cannot rotate along the same value as the intuitive angle(i.e,the angle of incidence) so due to lack of required energy the reflected ray traverses a shorter angle
In fact tan(r)=e*tan(i)
e=coefficient of restitution
0<e<1 hence tan(r)<tan(i), so r<i
The question states no friction on the way to the wall. But, because the ball is hitting the ball at an angle, then it has forward momentum at impact. At this point, you take into consideration the verbiage about losing energy. You can equate this to an introduction of a spin on the ball after impact. The spin reduces the ball's speed away from the wall therefore generating a lesser angle than the incident.
As internal energy becomes less, it tends less to move forward which makes the emergent angle lesser.
energy lost in the collision decreases the speed of the ball which is like light refraction so the angle of incidence is greater than angle of reflection (refraction in this case)
Would it be more useful to think of angle of incidence and angle of reflection as subtended between the normal to the wall and the path of the ball?
but light doesn't lose energy when its reflected from the mirror does it ?? so if we Suppose that the ball will not lose energy or speed when its collide . so the angle of reflection must equal to the angle of incidence . so why this unsure is Incorrect ?? .
For this analogy, wouldn't the angles have to be measured from a normal line?
Log in to reply
I agree...doesn't the explanation imply the the theta(r) in the diagram would get smaller, and the "real" angle of reflection gets greater?
Log in to reply
I was thinking that when I answered and therefore answered wrong.
Break the speed of the ball down into two components: one going horizontally and parallel to the wall, x , and one going vertically and perpendicular to the wall, y . Kinetic energy, and thus the speed, will be conserved on x component, but y will lose some speed. This is because the wall can only apply a force in the y direction, so the ball can only waste energy in that direction.
Imagine a right triangle, with x as the base and y as the height. After the collision, x will stay the same, however y will decrease, therefore the angle after the collision also decreases.