Cut and Flow
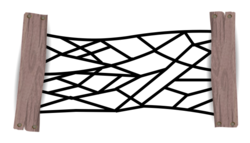 What is the least number of cuts that must be made in order to completely cut through this rope fence?
What is the least number of cuts that must be made in order to completely cut through this rope fence?
Note: The knots where multiple ropes meet are too thick to cut through. There is a beautiful way to solve this that is much more elegant than randomly attacking the fence with scissors.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
I got that with 3 cuts
Prove your answer.
can be done in 4 cuts -.-
I found a way to do it in 3 if intersections are used.
4 cuts to me. First 3 cuts are as drawn and the fourth cut located in the intersection of the 4th and 5th line
2,3 & 4,5 form knots. so only 3 cuts are sufficient......
Read the whole problem, You can not cut any knot
I got it completely cut in just 3 cuts, but had no such option in list of answers.
I did it in 4.
Can you post a picture of the cuts you used?
My guess is that you interpreted the problem in such a way that your 4 cuts don't separate the two sides of the fence fully. The diagram of 5-streams of flow is a proof that 5 cuts are necessary to do that. Since the 5 paths are independent (use completely different edges), and each path must be cut at least once in order to have fully broken the fence, at least 5 cuts are necessary to completely separate the two sides.
@Zandra Vinegar – Hi, sorry, I didn't read the part about the knots being too thick to cut through. I Think Alexander might have something to say about this ;-)
Can you post a picture of the cuts you used?
My guess is that you interpreted the problem in such a way that your 3 cuts don't separate the two sides of the fence fully. The 5-streams of flow is a proof that 5 are necessary to do that. Since the 5 paths are independent (use completely different edges), and each path must be cut at least once in order to have fully broken the fence, at least 5 cuts are necessary to completely separate the two sides.
I think they cut by 3 and jump over the rope :P
I am unable to find any option for posting a picture in the comments section here. In case you know how we can do it then will you please guide me regarding the same so that I can share a picture of my solution here.
@Nikhil Dhawale – Also I read the problem again closely and I realised that I had been cutting at the knots which is not permitted. So well yes 5 is the right answer.
I just looked at the spot with the fewest ropes crossing.
Simply the best, The cut must pass 2 times for first area, and another 1 time for each next area. So The number of cuts are number of area that cut pass plus 1, for example cut pass 4 area must use 4+1 cut = 5 cuts. That's all.
So I don't know anything about Graph Theory, but I'd like to share my thinking on how I solved this.
Firstly, I recognized that you'd have to cut at least one string from both top and bottom. Then, looking at the middle, what I can observe immediately without counting all possible cuts is that you'd need more than 1 cut to cut across from top to bottom; therefore, the minimum cuts you'd need based on these minimal observations is 4. Next, I looked at the clustering of strings. On the left, you can safely infer you'd be making way more than 4 cuts. On the right, however, there's less clustering. This way I've localized where to look. The next step for me then is to check if I can make 4 cuts, which as I found out, you can't. Then, I checked for a way to make 5 cuts. I only needed to confirm there is one. A tip is that the long rectangles allows you to traverse from top to bottom farther, cover more distance across than other paths. Lastly, I double checked to see if 4 cuts was valid, then, voila!
For each closed loop, one cut in + one cut out = 2 cuts through. For two adjacent loops, at the common side : one cut out = one cut in. Then a cut through = numbers of loopsx2 - numbers of common side : 2x2 -1 = 3. So we have to find a path that crosses the minimum adjacent loops from the upper side to the lower one. Then we have numbers of cuts = numbers of loopsx2 - (numbers of loops-1). Here we have 4 adjacents loops so numbers of cuts = 4x2 - (4-1) = 5.
This problem and solution is a small example of a beautiful duality in graph theory and linear programming: Max-Flow/Min-Cut.
Instead of guessing rope-segments to cut, on this graph it's much easier to draw in horizontal paths that connect the two posts: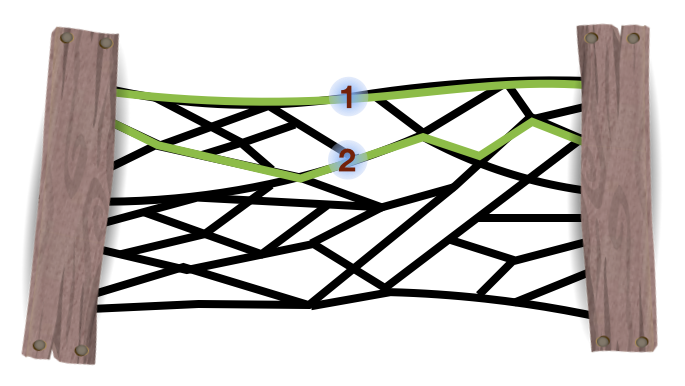
Try to draw as many horizontal lines as possible without ever reusing a length of rope. Wiggle around and refine your lines as needed to fit in as many as possible. This is called the "Max-flow" perspective, and that terminology hints at a different interpretation of the situation: If each of these ropes were instead a hose with a flow capacity of 1cm of water/second, how much water-per-second could be pumped from the left of the system to the right? Turns out this question has the same answer as our Min-Cut challenge: 5 paths = 5 cuts! And it's much easier to find the solution for this particular graph from the max-flow perspective.
Here are 5 example paths: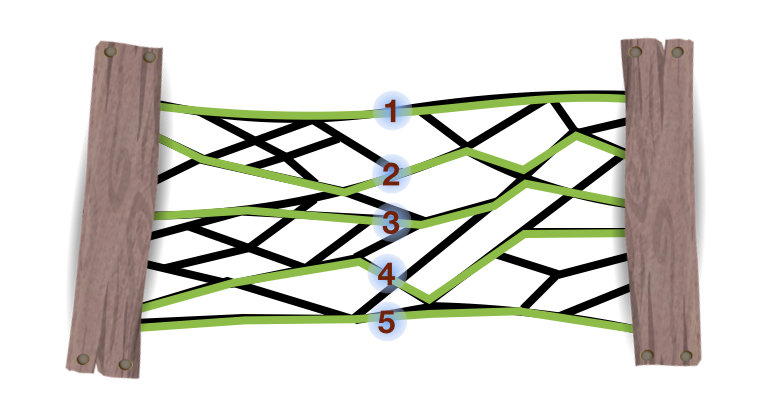
Finding these 5 paths means that at least 5 cuts will be necessary, since we have to cut across each somewhere in order to separate the fence. So, this 'max-flow' diagram of horizontal lines serves as a proof that "at least 5" is as good as we can do in terms of cuts. And drawing and refining the horizontal lines is also a great method for finding a minimal set of edges to cut. Just look for segments on each horizontal path that are on a region also bordered by the path above and the path below:
These 5 cuts work! At least 5 cuts are necessary. QED!