Cut it!
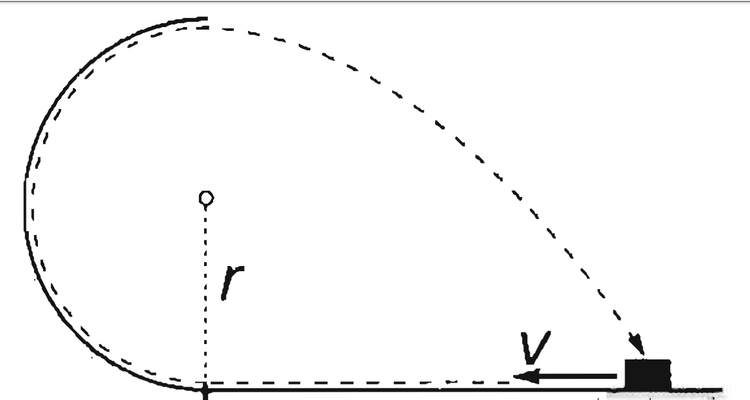 A frictionless track consists of a
horizontal part of unknown length, which connects
to a vertical semicircle of radius r . An
object, which is given an initial velocity v , is
to move along the track in such a way that after
leaving the semicircle at the top it is to fall back to
its initial position. What should the minimum length
of the horizontal part be '?
A frictionless track consists of a
horizontal part of unknown length, which connects
to a vertical semicircle of radius r . An
object, which is given an initial velocity v , is
to move along the track in such a way that after
leaving the semicircle at the top it is to fall back to
its initial position. What should the minimum length
of the horizontal part be '?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If you apply the condition for complete vertical circular motion , i.e v = 5 g r , won't the particle complete a Circular motion and not the loop like motion that's asked in the question ?
Log in to reply
After it had reached the top there would be nothing to provide centripetal acceleration for circular motion.
Log in to reply
So, what do you wanna say ?
Log in to reply
@Arpit Agarwal – See, if we give the particle a velocity of 5 g r , it will just be able to make it to the topmost position. At the topmost position, the outward force, i.e. the centripetal force( r m v 2 ) will be just equal to it's weight. Now, had there been a complete circle, the particle would have gone forward because of it's inertia of motion. Since, in this case, there is no path left, it follows inertia, and escapes the circle.
After escaping, now, it is only under the action of GRAVITY, and so it follows a parabolic trajectory.
Log in to reply
@A Former Brilliant Member – Now I understand , thanks :)
Log in to reply
@Arpit Agarwal – No problems!!:):)
Log in to reply
@A Former Brilliant Member – Actually , one more thing , in case of a small object tied with a string to a pt. and it undergoes vertical circular motion , what happens ? Is it because of the velocity of 5 g r does it complete the circular motion or inertia . It doesn't stop at the topmost point, does it ?
Log in to reply
@Arpit Agarwal – See, for any object to complete a circular motion, it just needs to reach the top with enough velocity, after which the gravity will do it's work. When we give this velocity, we provide the particle enough kinetic energy to reach the top with still some of the velocity left. Due to this energy, it tries to go forward, and the string becomes taut again, hence providing tension, which then acts as the necessary centripetal force, and the body completes the circle...
Log in to reply
@A Former Brilliant Member – I'll remember that . Thanks :)
Log in to reply
@Arpit Agarwal – Again...No probzz!!:):)
Log in to reply
@A Former Brilliant Member – And thanks for following me!!:):) @Arpit Agarwal
I did it the same way
Centripetal force = r m v 2 and the weight acting downwards is equal to m g . These forces must be equal at the top of the loop so r m v 2 = m g ⇒ r v 2 = g ⇒ v = g r . Now using distance = speed × time: v 2 = t 2 d 2 = t 2 ( 2 r ) 2 ⇒ 4 r 2 = g h t 2 ⇒ t = g r 2 r Finally vertical displacement... = v t = g r × g r 2 r = 2 r
This is the method I used
Alright listen up you Asian nimwhits. Prepare to get your minds blown and get taken on a ball wrenching trip to the land of intellectual bliss. I'm an American so you better listen up.
Firstly the change in x after coming out of this daggum circle is equal to its velocity tangent to the circle as it's initial x velocity and then its just a simple free fall problem.....Like the free fall India took when Britain made y'all their slaves.
so basically Velocity is 2 pi R over T and then when you multiply that by T your times cancel making it two.
Merica.
Hahaah hahaah, you need medical support buddy. You are suffering from superiority syndrome.
Minimum condition will be satisfied, when the minimum condition for loop-a-loop will be satisfied. And as we know, this is possible only when the velocity at the bottom will be equal to the minimum velocity for loop-a-loop, i.e. 5 g r , where g is the acceleration due to gravity, and r is the radius of the circle.
Now, by using energy conservation:
Energy at the bottom = Energy at the top
Using, ground as reference frame, Energy at bottom = 2 1 m ( 5 g r ) 2
Energy at the top = m g ( 2 r ) + 2 1 m v 2 , where 2 r is the body's height from the reference, and v is it's velocity.
Since there are equal, solving the equation, v comes out to be g r .
Now, after this point, the body will continue to go, and will follow the path of a horizontal projectile, whose height from the ground is 2 r , initial velocity = g r , and whose Range is what we need to find.
Since in a horizontal projectile,
R a n g e ( R ) = u g 2 h ⇒ R = g r g 2 ( 2 r ) ⇒ R = 2 r r ⇒ R = 2 r