Cut Through the Circle

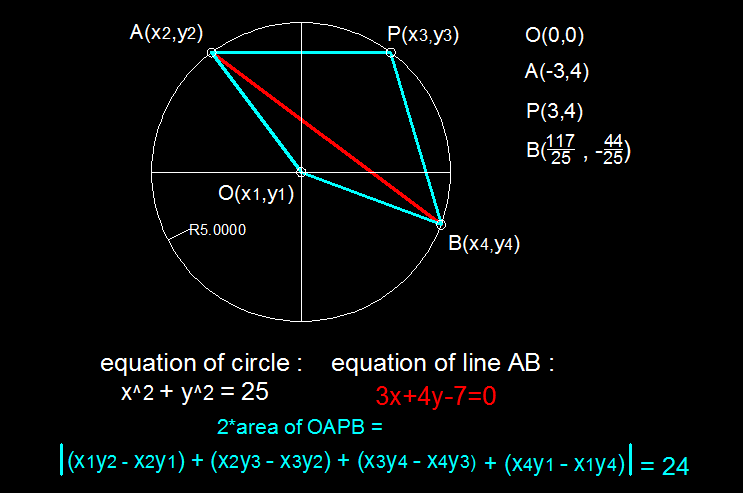
The circle $O$ has its radius = $\sqrt{3^2 + 4^2} = 5$ as $P$ is on the graph itself.

Now, from the image above, if we draw another diagonal (yellow) $OP$ , the slope of this line will equal to: $\dfrac{4 - 0}{3 - 0} = \dfrac{4}{3}$ .

On the other hand, we can rewrite the red line $l$ as: $3x + 4y - 7 = 0; y = (\dfrac{-3}{4})x + \dfrac{7}{4}$ .

The slope of $l$ = $\dfrac{-3}{4}$ .

Therefore, the product of the slopes of both lines = $-1$ . That means these diagonals are perpendicular to each other at intersection point $C$ .

Then since $AO$ and $BO$ are radii of the circle, $AO = BO$ , and the $\triangle AOB$ is an isosceles triangle. Furthermore, the line that is perpendicular to the isosceles' base ( $AB$ in this case) will be the bisector of the base also: $AC = CB$ .

Hence, $PC$ is also a bisector of the $\triangle APB$ because $AC = CB$ and $PC \perp AB$ . That is, the $\triangle APB$ is also an isosceles triangle.

Thus, $AOBP$ is a kite.

Therefore, the area of the kite $AOBP$ = $\dfrac{1}{2}\times AB\times OP$ .

Then by using Pythagorean theorem, $AO^2 = AC^2 + CO^2$ .

By using the line-point distance formula, we can evaluate $CO$ : $\dfrac{|3\times 0 + 4\times 0 - 7|}{\sqrt{3^2 + 4^2}} = \dfrac{7}{5}$ .

Thus, $AC^2 = AO^2 - CO^2 = 5^2 - (\dfrac{7}{5})^2 = (\dfrac{24}{5})^2$ ; $AC = \dfrac{24}{5}$ .

Finally, the area of the kite $AOBP$ = $\dfrac{1}{2}\times (2\times \dfrac{24}{5})\times 5 = \boxed{24}$ .