Cute Little Shuriken
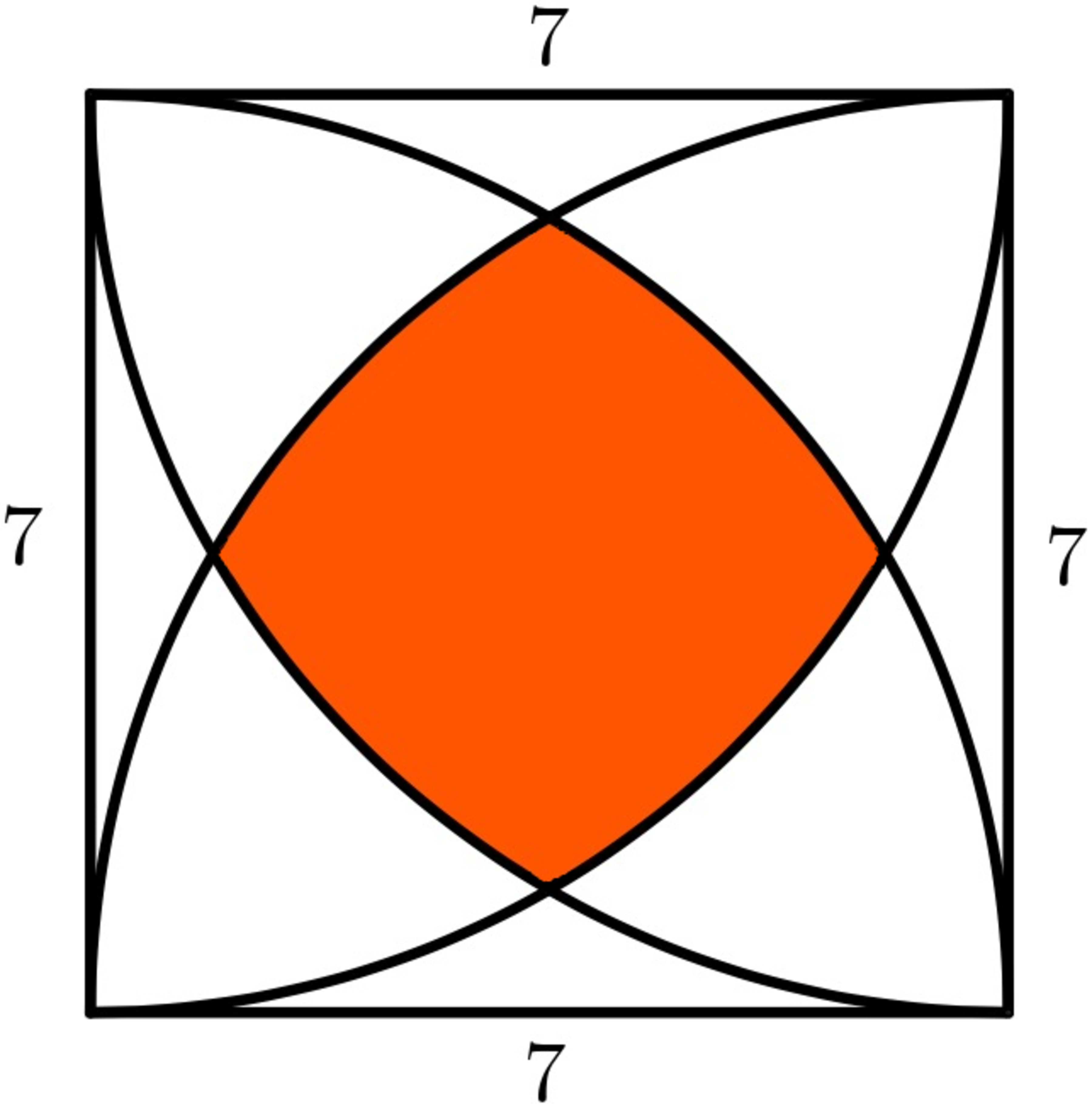
Find the area of the region colored in orange.
For your final step, use the approximation π = 7 2 2 .
Give your answer to 1 decimal place.
The answer is 15.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Exactly the same as this question , I just took my answer from here and substituted the side of the square to get my answer
Log in to reply
Log in to reply
Popped up in my problems of the day
Log in to reply
@Hung Woei Neoh – LOL, that's just coincidence
Log in to reply
@Jason Chrysoprase – Exactly. Anyway, I solved it the same way as you XD
Log in to reply
@Hung Woei Neoh – Which one solution is easier to you, mine or the others ?
Log in to reply
@Jason Chrysoprase – I dunno. It depends on how you see the shapes and what theorems or formulas you know
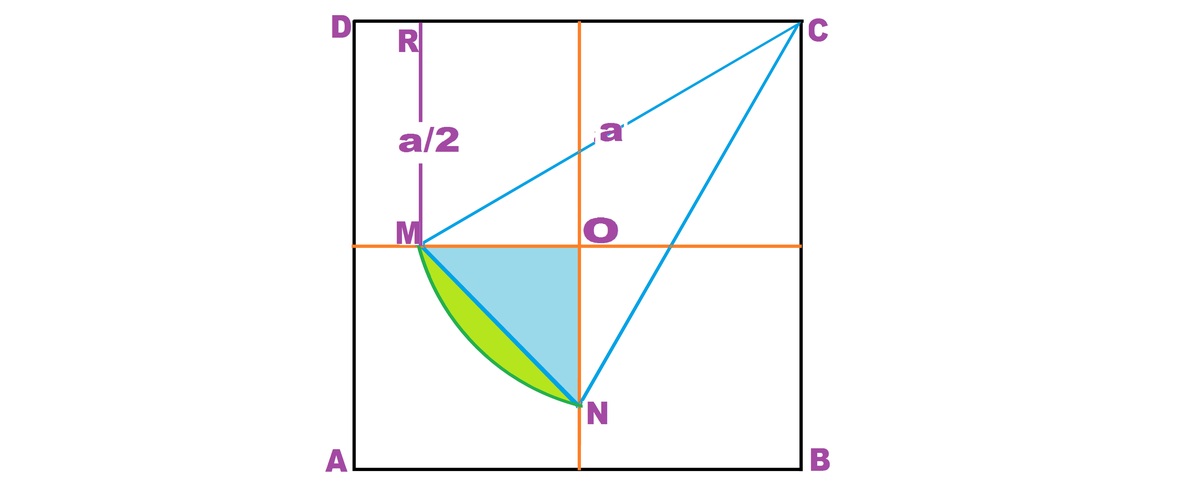 ABCD is a square with sides a. O is the center. It is divided ito 4 equal squares.
A quarter of the flower is shown as area OMN.
L
e
t
M
R
⊥
C
D
.
I
n
r
t
.
Δ
M
C
R
,
2
R
M
=
H
y
p
.
M
C
.
⟹
∠
M
C
R
=
3
0
o
∵
o
f
s
y
m
m
e
t
r
y
,
∠
B
C
N
=
3
0
o
.
C
l
e
a
r
l
y
∠
N
C
M
=
3
0
o
.
∴
Δ
M
N
C
i
s
a
−
3
0
o
−
a
.
C
R
=
2
3
a
,
∴
M
O
=
2
3
a
−
2
1
a
.
R
e
q
u
i
r
e
d
a
r
e
a
=
4
∗
{
a
r
e
a
C
M
N
}
=
4
∗
{
a
r
e
a
o
f
s
e
c
t
o
r
N
C
M
−
(
a
r
e
a
s
o
f
Δ
s
M
O
C
a
n
d
N
O
C
)
}
=
4
∗
{
π
∗
a
2
∗
3
6
0
o
3
0
o
−
2
∗
2
1
∗
M
O
∗
2
a
=
3
a
2
(
π
+
3
−
3
3
.
)
a
=
7
a
n
d
π
=
2
2
/
7
,
s
u
b
s
t
i
t
u
t
i
n
g
w
e
g
e
t
a
r
e
a
=
1
5
.
4
6
2
8
.
This is the copy of my solution of the problem 4 months ago.
ABCD is a square with sides a. O is the center. It is divided ito 4 equal squares.
A quarter of the flower is shown as area OMN.
L
e
t
M
R
⊥
C
D
.
I
n
r
t
.
Δ
M
C
R
,
2
R
M
=
H
y
p
.
M
C
.
⟹
∠
M
C
R
=
3
0
o
∵
o
f
s
y
m
m
e
t
r
y
,
∠
B
C
N
=
3
0
o
.
C
l
e
a
r
l
y
∠
N
C
M
=
3
0
o
.
∴
Δ
M
N
C
i
s
a
−
3
0
o
−
a
.
C
R
=
2
3
a
,
∴
M
O
=
2
3
a
−
2
1
a
.
R
e
q
u
i
r
e
d
a
r
e
a
=
4
∗
{
a
r
e
a
C
M
N
}
=
4
∗
{
a
r
e
a
o
f
s
e
c
t
o
r
N
C
M
−
(
a
r
e
a
s
o
f
Δ
s
M
O
C
a
n
d
N
O
C
)
}
=
4
∗
{
π
∗
a
2
∗
3
6
0
o
3
0
o
−
2
∗
2
1
∗
M
O
∗
2
a
=
3
a
2
(
π
+
3
−
3
3
.
)
a
=
7
a
n
d
π
=
2
2
/
7
,
s
u
b
s
t
i
t
u
t
i
n
g
w
e
g
e
t
a
r
e
a
=
1
5
.
4
6
2
8
.
This is the copy of my solution of the problem 4 months ago.
The area of the shaded region is: 3 a 2 ∗ ( 2 2 / 7 + 3 − 3 3 ), where a = 7 . We can draw a square inside the orange area whose side is equal to a 2 − 3 by using Pythagoras's theorem. Hence, the area of the square is a 2 ( 2 − 3 ) . Also, the area between our square and the orange area is: 4 ( t h e a r e a o f t h e f o u r c i r c u l a r s e c t o r s = 4 ( 1 2 a 2 ) ( 7 2 2 -3)).
Thus, total area of the orange part: 7 2 ( 2 − 3 ) + 4 ( 1 2 7 2 ) ( 7 2 2 - 3) = 3 7 2 ( 2 2 / 7 + 3 − 3 3 )= 15.5
x + y = Sector Area − Segment Area
= ( x + y + n ) − n = 3 6 0 3 0 × π × 7 2 − ( 3 6 0 6 0 × π × 7 2 − 4 3 × 7 2 ) = 1 2 4 9 × 7 2 2 − ( 6 4 9 × 7 2 2 − 4 4 9 × 3 ) = 6 7 7 − 3 7 7 + 4 4 9 3