Halving your cake and eating it too
 What is the maximum number of pieces it is possible to cut a rectangular prism shaped cake into with 3 cuts without moving (or rearranging) the pieces or stacking them up?
What is the maximum number of pieces it is possible to cut a rectangular prism shaped cake into with 3 cuts without moving (or rearranging) the pieces or stacking them up?
Clarification: All cuts must be straight.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
The problem i have with this question is that i assumed essentially the entire problem. Didnt like it at all. I see why its eight and had it as an answer but chose seven because i thought we could only cut on the top surface assuming that it was a circle you could make cuts to make a smaller triangle such that the cuts overlap each other making a small arc shaped slice and two more pieces on each end of it giving you 7 slices of non equal size. Problems need constraints.
Log in to reply
I agree. The question specifically says the pieces cannot be stacked. By virtue of the proposed 3rd cut parallel to the top, pieces become stacked. That breaks the "no stacking" contraint
Log in to reply
Stacking the cake would involve picking up a piece and placing it on top of the cake, cutting the cake lengthwise is not stacking.
Agreed ...it is 7
But you did not do the stacking, so it doesn't count. But yeah, that latter part is redundant and confusing.
huh Write a comment or ask a question...
but in question they specify "without moving the pieces or stacking them up" than how ?
Nice question. This is known as the Cake number . Imagining the cake as a cube, using n planes the cake can be cut into 6 n 3 + 5 n + 6 pieces.
Log in to reply
Sir, how to use this generalization ? and how to get it ?
Here's my thing... I got 8, but I answered 7. I figured 8 counted as stacking the pieces. I understand that cutting the pieces so that they end up stacked and stacking the pieces before cutting them are two different things.
However, if you were to physically stack the pieces, that would also be moving the pieces, making the "or stacking them up" redundant.
Therefore, I assumed by saying "stacking them up," the author meant cutting them in a way such that they end up in a stacked position.
This was the conscious thought process; it's not like I didn't realize what I was assuming and thus got it wrong.
I think "or stacking them up" should be removed.
It wasn't explicitly stated that cuts can be on any surface.
If we're allowing curved cuts then I can get 10 slices. Simply cut three horseshoe shaped cuts into the cake with each cut being 120 degrees away from the last.
Log in to reply
If we are allowed to make irregular cuts you can get an infinity of pieces.
Log in to reply
I came to the same conclusion, but stopped when i read the amendment of "all cuts are straight lines".
by making wavy lines it would approach infinity limited only by the consistency of the cake and thickens of the knife
can you please explain with a pic
Yes, though the question is wrongly written. If it hard merely said "without moving the pieces" this would have been fine, as it would mean you couldn't cut the cake in half, put one halve on top and cut again etc.
By adding th word stacking, it implies that the cut does not allow a stack to be created. It is no use being clever in the answer if the English usage in the question is ambiguous to say the least.
This is the third time recently I have clicked on a featured question to find poor quality thinking. A complete waste of time and irritating.
Cutting along the side without stacking? My cake is just an inch tall and I cant cut it that way. I should stick to 7 because the solution of 8 made cake stacked already.
Log in to reply
It also does not specify "straight" cuts or shape of the cake. Take a round cake and cut it into quarters then cut a circle in the top. You can end up with icing on all of the slices and 8 almost equally sized portions.
Log in to reply
I just need 2 wavy cuts. One across another will create more than 10 irregular slices. If we are not talking about straight cuts, the given situation then is rubbish.
At the end of the question it said all lines must be straight
Stacking is the act of making a stack, no matter how you do it. If cutting the cake along the side results in stacks, then, by definition, it is stacking.
This is worded very poorly. End of discussion.
Honestly, has anyone here seen a cake cut with perfect straight lines? Lol. The posted solution is incorrect given that the end result has stacked cake pieces. But you making that third cut, you are creating a stack. I'm tired of all the horrible questions on this site. This one takes the cake, and I'm done here.
It also does not specify "straight" cuts or shape of the cake. Take a round cake and cut it into quarters then cut a circle in the top. You can end up with icing on all of the slices and 8 almost equally sized portions.
I SEE WHERE THEY GET THE 8 PIECES TOTALALY DECIEVING
Question specifically says the pieces cannot be stacked. Than the answer should be 6
I agree that this is stupid. If we're going to get non-conventional cutting into the center of the cake then it can be taken further.
Suppose you cut the cake diagonally from top left to lower right, then again from top right to lower left (the side facing you will now look like an x).
Then for the 3rd cut, I go horizontally from below the "x" but above the bottom on the frontside, cutting diagonally back to above the "x" but below the top on the backside.
Such straight cuts would result in 10 pieces, you can see this by drawing a box with an x, a horizontal line below and above the intersection, which is the side view.
This just goes to show that if you're taking 3rd dimension into account that it's actually more than 8.
my answer is 8 as there is 8 octants
Log in to reply
You are right with 8. The same way I'm thinking ... if we are cutting cheese, But cake has icing which leads me to look at it as a 2-D object, and the max number of pieces is 7. Unless four of the guests have to eat the bottom of the cake. The authors did not make a good quality problem. Sorry!
Cut the cake into 4 parts from top view using 2 cuts. Make the 3rd cut from the side view/front view thus giving you 8 pieces of cake.
But then four people don't get frosting :(
This breaks one of the questions constraints. By virtue of the 3rd cut, pieces are stacked. That is not allowed.
Log in to reply
Make the 3rd cut first then. Simple.
Log in to reply
It is still a stack the moment you make the horizontal cut. There is one piece stacked on a second piece (or there are 4 pieces stacked on 4 other pieces.) The order of the cuts doesn't change the stacking effect.
Log in to reply
@Jim Schowalter – True, but you didn't stack the pieces. The wording says "without stacking". You create stacked pieces but you don't stack the pieces. That's the lawyer side of me talking :) (Not really a lawyer, I just like to think I am!)
Log in to reply
@Bill Glidden – If you killed someone by accident, you are still accountable for manslaughter. If you cut the cake resulting to stacked pieces, it is still stacking. (I'm not a lawyer)
First cut is horizontally across the middle of the cake as if to make two cakes, one on top of the other. The remaining two cuts are vertically, at any angle to one another, but at 90 degrees to one another if you want equal sized pieces, down through both upper and lower halves of the cake. This gives 4 pieces in the upper layer and a further 4 in the lower layer, making 8 pieces in total. You are not stacking the pieces by moving them, which is what is meant by the constraint. I was always taught to answer the question I was asked, not the one I would like to have been asked.
You are right with 8. The same way I'm thinking ... if we are cutting cheese, But cake has icing which leads me to look at it as a 2-D object, and the max number of pieces is 7. Unless four of the guests have to eat the bottom of the cake. The authors did not make a good quality problem. Sorry!
If the cuts have to be straight lines, you can make 8 pieces by quartering the base along the "sagittal" and "coronal" planes, and then halving along the "transverse" plane.
If you cut the base in half and then slice a sine wave (in one stroke since it's a continuous curve) through it as shown below, you can have many more pieces when you split along the transverse.
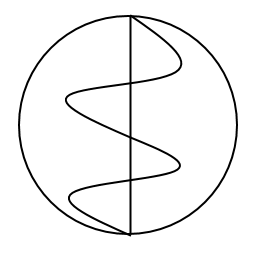
Just like a 2x2x2 rubik's cube.
You are right with 8. The same way I'm thinking ... if we are cutting cheese, But cake has icing which leads me to look at it as a 2-D object, and the max number of pieces is 7. Unless four of the guests have to eat the bottom of the cake. The authors did not make a good quality problem. Sorry!
So easy furst cut twice fron up and then from middle
This breaks the constraint where pieces cannot be stacked.
Log in to reply
The problem never stated that they cannot be stacked; it just said that you can't stack them up. Cutting a block along the side into two smaller pieces is not considered stacking pieces up.
Log in to reply
It also didn't state that a cut had to be a straight line. How many pieces do you think you could make without the straight line constraint.
Log in to reply
@Andy Jones – Let me say it a different way. If the only stacking restricted by the question is the stacking produced by moving a piece, then the constraint is redundant. Since the assumption is that the constraint is not redundant, then the no stacking implies that a stack cannot exist in the solution.
Log in to reply
@Jim Schowalter – The constraint was intended to be redundant; that was the key to the problem.
@Andy Jones – It should be implied that knives are straight and unbendable.
Log in to reply
@Alex Li – Get a cake and a knife and see how easy it is to make a cut that is not straight. Then get a piece of wood and a saw and see how easy it is to make a cut that is not straight. Then realize that nothing is implied.
Log in to reply
@Andy Jones – Maybe if you had a calmer attitude and didn't try to be so nit-picky you would have more than 2 followers.
Log in to reply
@Alex Li – I am calm. And I am not interested in having followers. You'll understand that is not important when you are older.
The problem says without moving them or stacking them up. I originally thought as you did that the problem did not say that cutting the cake into stacks was against the rules. But if that is the case, it would seem that not moving them would eliminate the need to discuss stacking as that would be redundant. So I am listening to others and now agree with them about the stacking issue, therefore, the correct answer is 7.
By the way, you are defending this problem as if you wrote it. Did you?
Log in to reply
@Andy Jones – Do you really think I didn't write it? See for yourself.
Log in to reply
@Alex Li – that explains why you are so defensive about this. Enough beating this dead horse.
Log in to reply
@Andy Jones – Agreed. Don't beat the dead horse. It makes them smell worse.
I respectfully disagree. There is nothing about what stacks, just no stacking. If a stack exists at the end, then stacking was done (perhaps by the knife, but this still breaks the constraint)
Log in to reply
@Jim Schowalter – The problem never stated that a stack cannot exist at the end. It just states that you cannot stack them up. If you cut the cake into 4, move the 4 pieces into a pile, and cut through them to get 8, that is considered stacking them up. I am sorry if you misunderstood the problem, but I don't want the 500+ people who solved it legitimately to lose credit.
Log in to reply
@Alex Li – Again, it does not state YOU cannot stack. It says "no stacking" Having a piece on top of another is stacking. By virtue of the cut, stacking is performed.
Log in to reply
@Jim Schowalter – "without moving the pieces or stacking them up" This is in no way equivalent to "the pieces cannot be stacked". When you make the 3rd cut, you are creating new pieces that are already stacked, not stacking the pieces up.
Log in to reply
@Alex Li – I gotta agree with Alex Li. The resultant pieces are "stacked". But the cutter didn't "stack" them. So that adheres to the spirit of the question, if not 100% to the letter of the question.
Log in to reply
@Bill Glidden – Agreed. By simply cutting the cake so that the pieces are not displaced from their original position, no deliberate "stacking" has been done by the cake-cutter. The more mathematically precise wording of the question would be: "What is the maximum number of regions into which a cake, in the shape of a cube, can be partitioned by exactly 3 planes?", the planes being the equivalent of straight cuts through the cake.
@Jim Schowalter – One could also say that cutting into the cake will most likely move the pieces a very small distance. But obviously, the question doesn't prohibit any cuts. So, one must examine the difference in the words "stacking" and "stacked". It's such a minor little difference but it's enough to make it allowable to do the horizontal cut. When you cut the cake that way, you aren't "stacking" the pieces. But the resultant pieces are "stacked". At least that's how I interpret it.
Log in to reply
@Bill Glidden – I get the distinction. The way I do a problem like this is ask myself before each action "Will this break a constraint?" So ignoring all the other cuts... On the horizontal cut... I ask "is a piece moving?" I can safely answer (noting your comment on this) "No." Then I ask "is stacking taking place?" Here I cannot safely answer "No."
To me, the act of cutting is creating a stack thus the act of cutting is stacking pieces. Each constraint is separate and each does not result in the same answer.
Log in to reply
@Jim Schowalter – I must, in the interest of fairness, concede that you have made an excellent point. With that said, I offer the following retort: "Yeah? Well who asked ya??" :)
@Bill Glidden – It also does not specify straight cuts. Cut it into quarters then cut a circle in the top. You can end up with icing on all of the slices and 8 almost equally sized portions
a cake is a 3 dimensional object therefore it must be treated like one. stacking is a verb and therefore cuts across the horizontal plane of the cake are allowed. two cuts in the vertical plane and one in the horizontal result in 8 pieces of cake. Questions like these are as much about the wording as they are about the math.
If someone asks me to take a single 3 dimensional object, cut it into two pieces and stack the pieces, is my only option to make a vertical cut and then to move one piece onto the other? I believe not. I believe, I can make a horizontal cut and have satisfied both requirements. With this, I would say that the act of cutting is also an act of stacking.
 I answered 8, but no matter what on Earth I try, I can only get 7. Now, if the cake had some sort of HOLE in the center, that's a completely different story.
I answered 8, but no matter what on Earth I try, I can only get 7. Now, if the cake had some sort of HOLE in the center, that's a completely different story.
The only solution I can think of here is that when the author says "moving the pieces" or "stacking" them, it means to deliberately move them (for example, cutting a cake in half, stacking them, halving the stack, and so forth). If the cake is not moved, cut into quarters, then cut down the center height-wise, 8 pieces will be made which RESULT in two layers, but the cake was not EXPLICITLY "stacked".
I just used math. I think if you don't cut the cake across the middle then you max out at 7 pieces. In the traditional sense of a 2d plane. If you cheat and cut into equal 25% pieces then cut through the centers you get 8. I used 2 cubed to get the answer since each time you make a cut you should be halving the pieces available, so 2-4-8.
Log in to reply
You are right with 8. The same way I'm thinking ... if we are cutting cheese, But cake has icing which leads me to look at it as a 2-D object, and the max number of pieces is 7. Unless four of the guests have to eat the bottom of the cake. The authors did not make a good quality problem. Sorry!
I used your method. I really don't care what the math says if there is no way to display the result than the math is incorrect. Of course if you cut it into quarters and then drop one of the pieces into a wormhole and send it to the gamma quadrant then make your third cut you get 3.1415926535 and then you can have some pi.
Make a criss cross cut on the z-axis (2 cuts, 4 pieces) then cut the cake in half on the x and y-axis (1 cut 4 more slices).
Cut an X then a straigth line through the middle. Its not a hard question.
Cut into quarters then cut diagonally from one corner to the opposite corner.
Cut the cake into quarters, then cut along the side.