Cyclic powers of 2! IMO 2015 problem#2
Find all positive unordered multi-sets of integers ( a , b , c ) such that a b − c , b c − a , c a − b are powers of 2.
If these sets can be represented as ( a 1 , b 1 , c 1 ) , ( a 2 , b 2 , c 2 ) , … , ( a n , b n , c n ) . Evaluate ⎝ ⎛ i = 1 ∑ n a i + b i + c i ⎠ ⎞ + n .
This is from IMO 2015-Problem #2.
The answer is 51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions

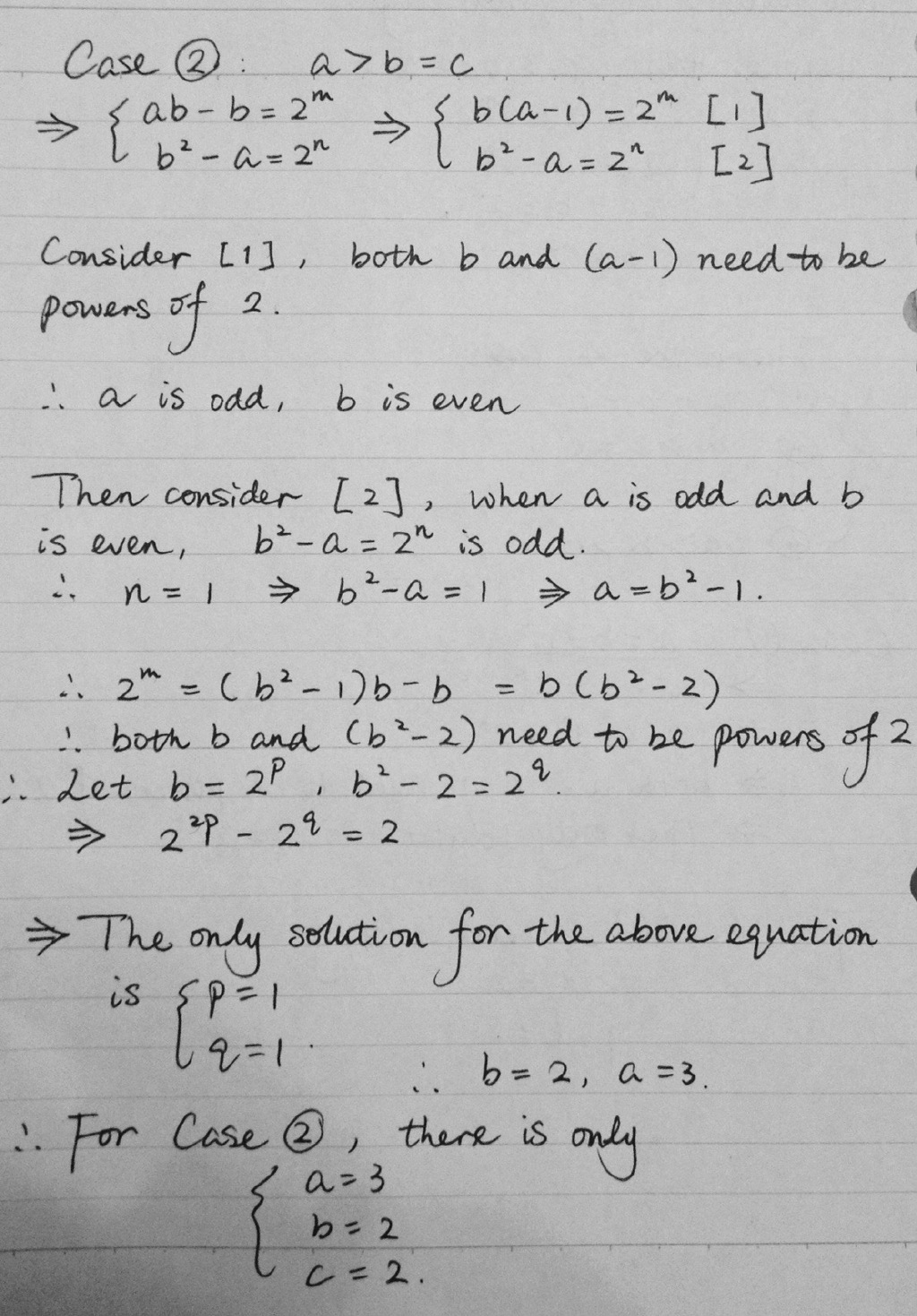

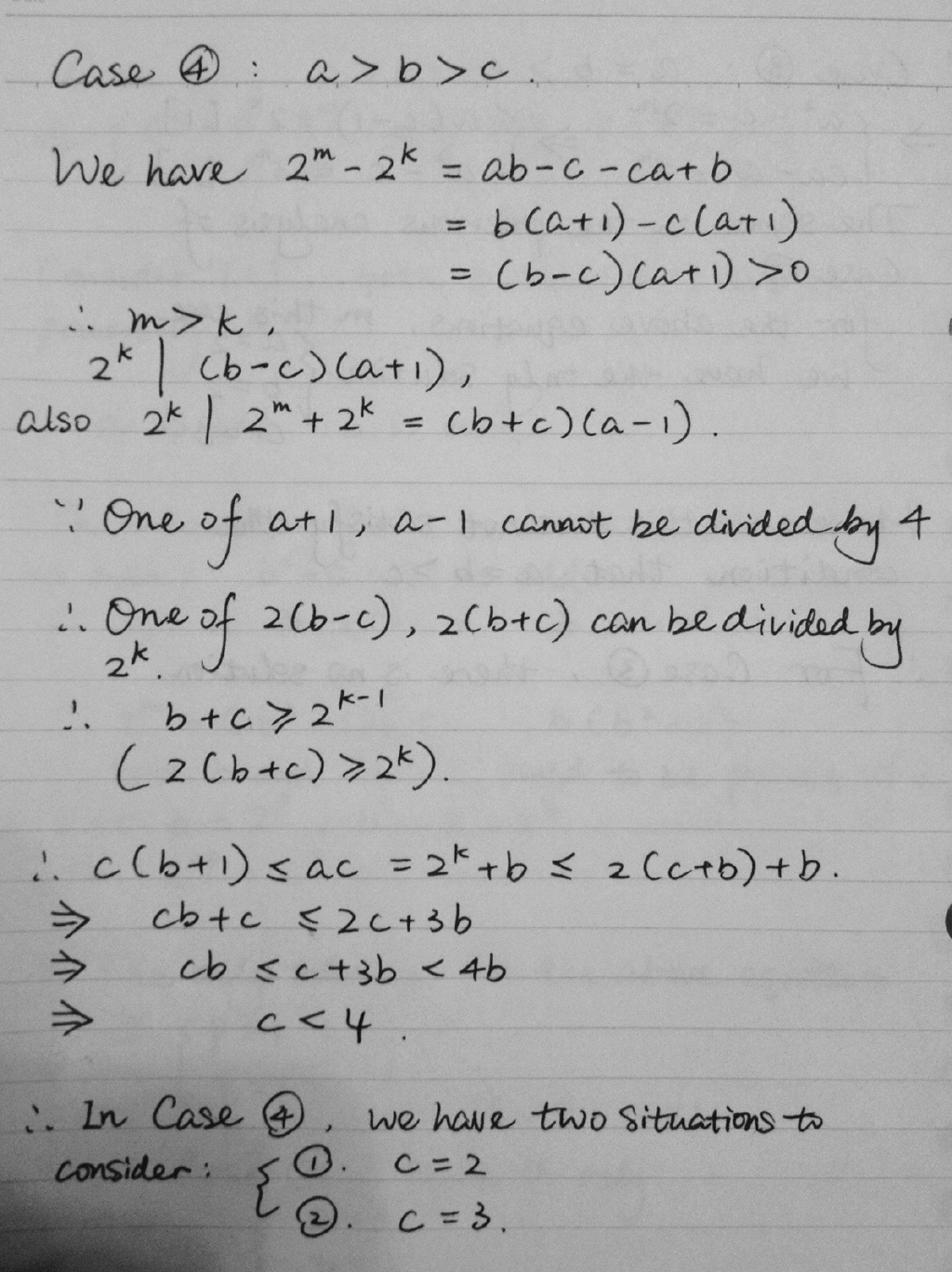
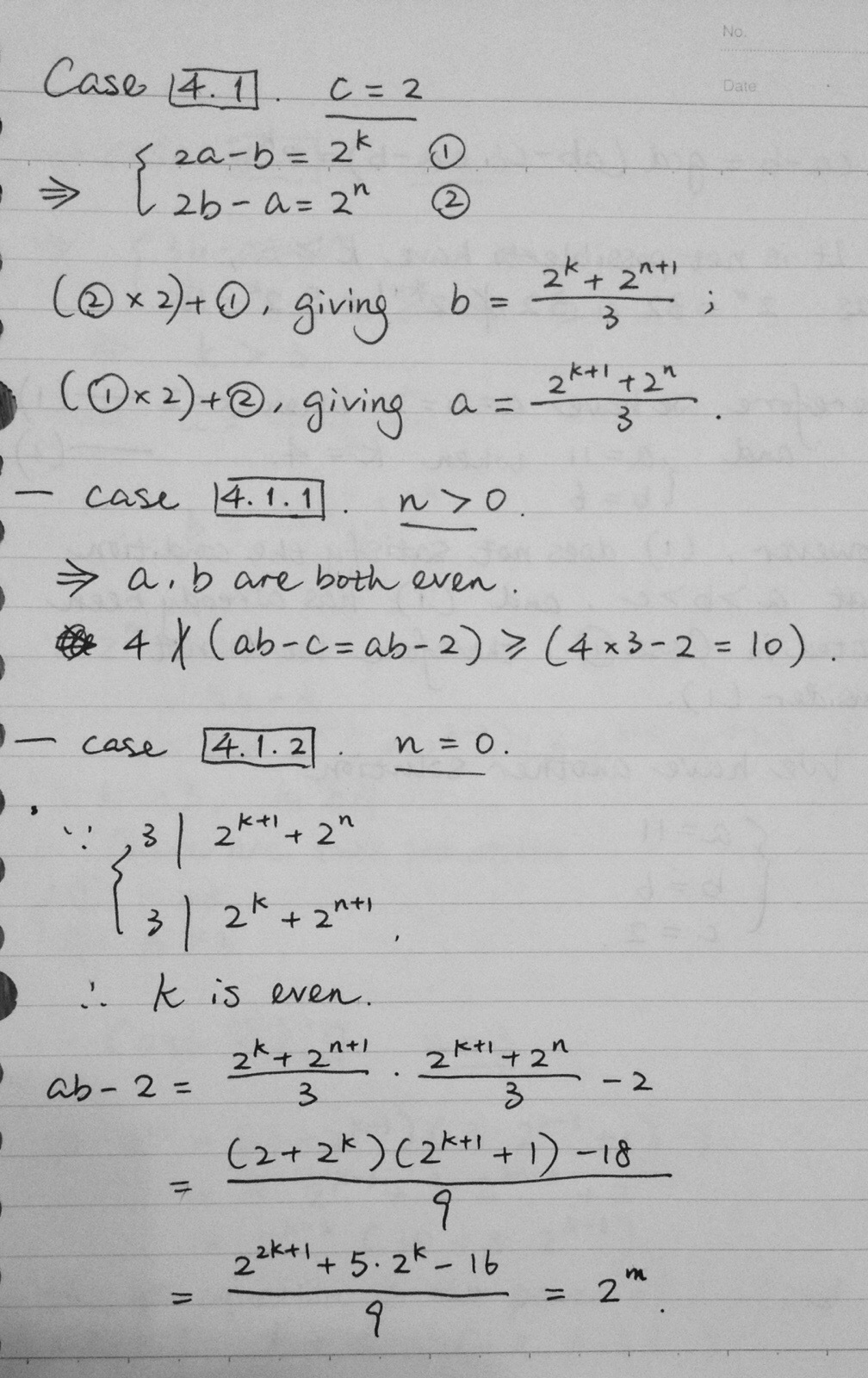

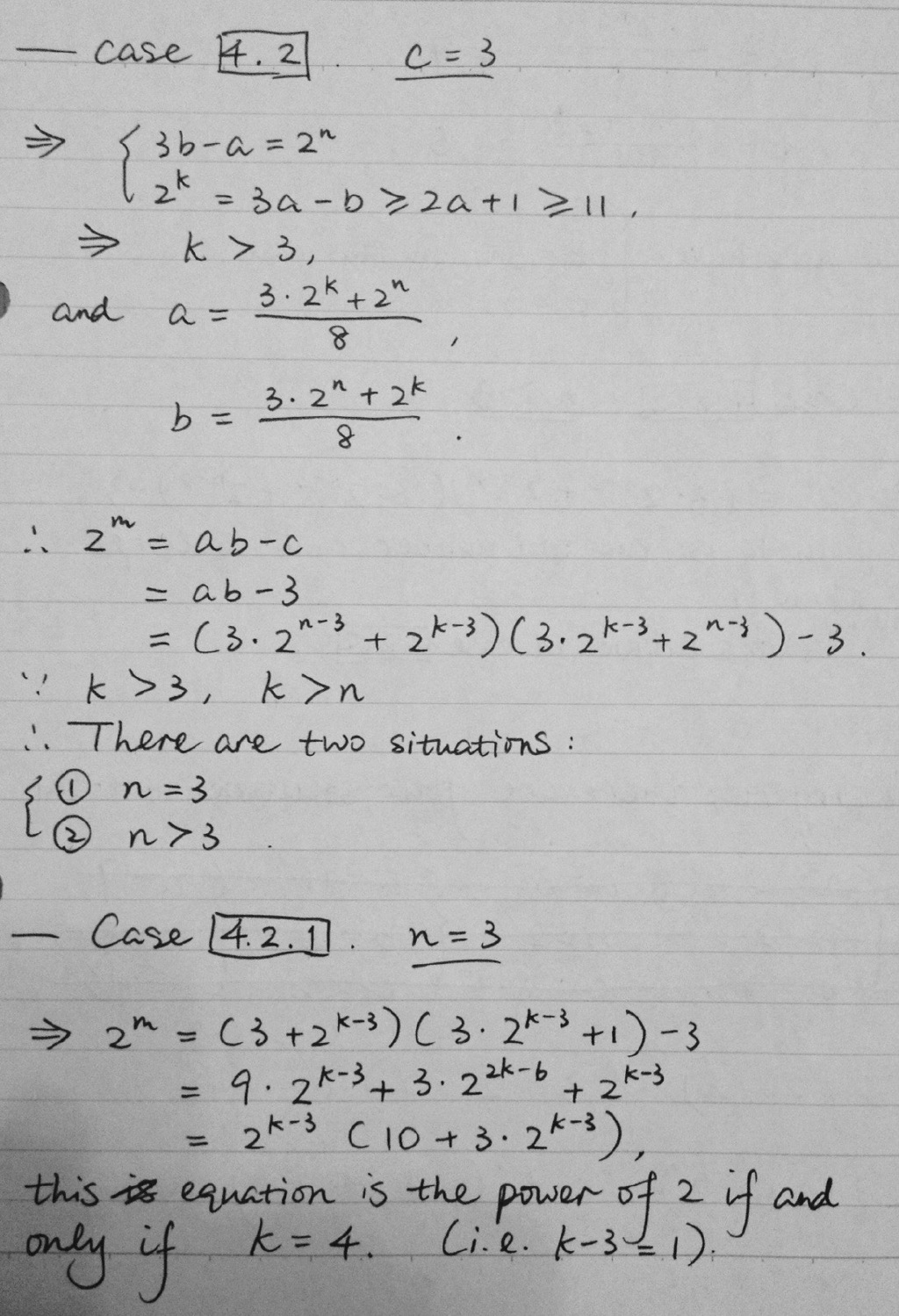
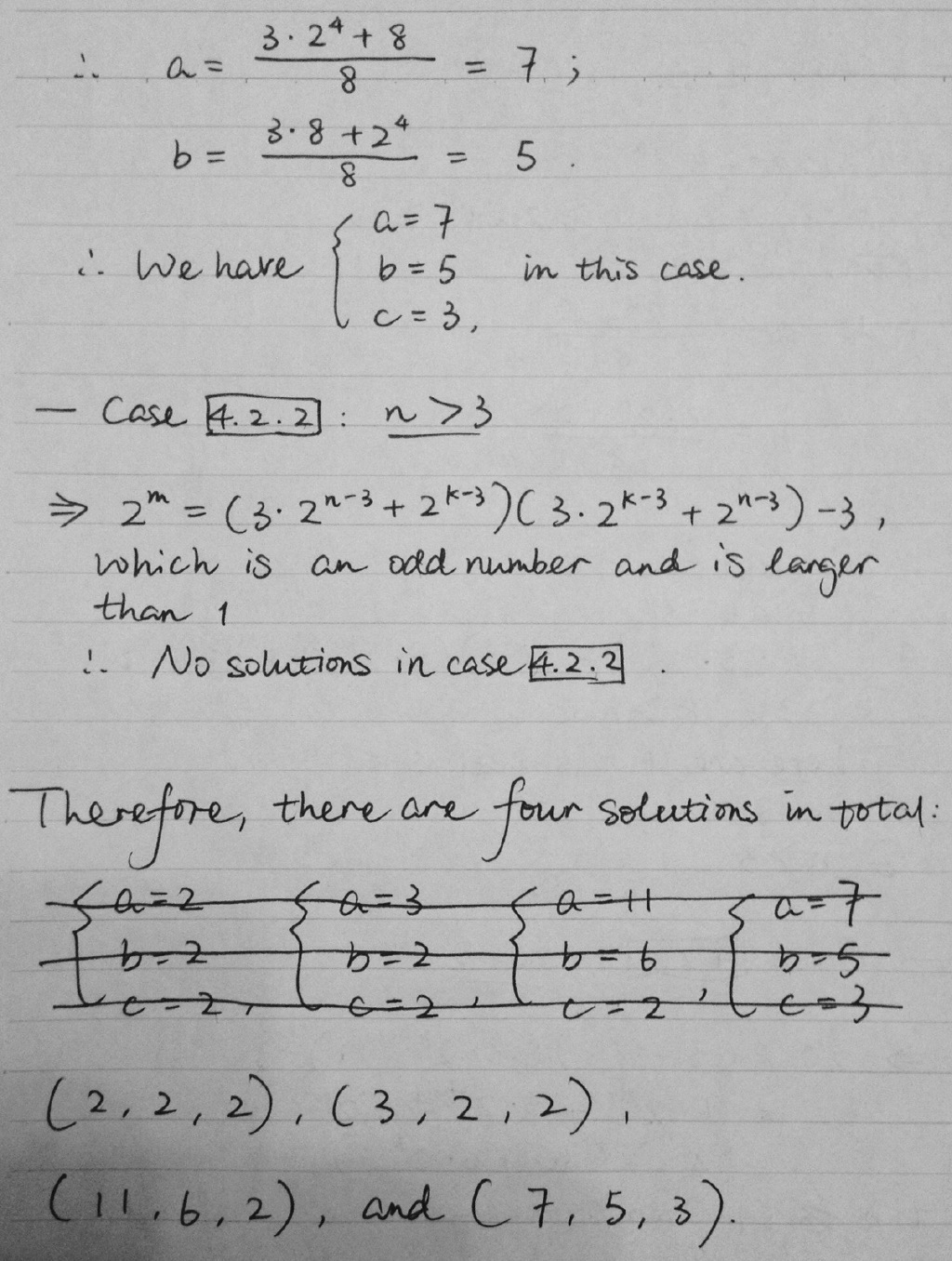
Great solution and good in covering case 4! which is the hardest case! The main thing however was to identify c < 4
If a = 1 ,then c − b and b − c both are powers of 2.It is impossible.
So a ≥ 2
Similarly b ≥ 2 , c ≥ 2
Here are two cases discussed.
Case 1 There are two equal numbers at least in them.
Might as well assume a = b
We have a c − b = a ( c − 1 ) is powers of 2.
∴ a , ( c − 1 ) both are powers of 2.
Let a = 2 p , c = 1 + 2 q ( p ≥ 1 , q ≥ 0 ) ,then a b − c = 2 2 p − 2 q − 1 is power of 2.
If q > 0 , 2 2 p − 2 q − 1 is odd,
∴ 2 2 p − 2 q − 1 = 1
∴ 2 q ≡ 2 ( m o d 4 )
∴ q = 1 , p = 1 , a = 2 , b = 2 , c = 3 .
If q = 0 , 2 2 p − 2 is power of 2,only p = 1 satisfied this case.
So, a = 2 , b = 2 , c = 2 .
We are easy to verify ( 2 , 2 , 2 ) , ( 2 , 2 , 3 ) both are satisfied.
Case 2 a,b,c are different from each other
Might as well assume 2 ≤ a < b < c
and b c − a = 2 α , a c − b = 2 β , a b − c = 2 γ , ( α > β > γ ≥ 0 )
1° a = 2
We prove γ = 0 at first.
If γ > 0 ,from a b − c = 2 γ ,we have that c is even.From a c − b = 2 β ,we have that b also is even.
Therefore, b c − a ≡ 2 ( m o d 4 ) ,but 2 α ≡ 0 ( m o d 4 ) .Paradoxical!
∴ γ = 0
∴ c = 2 b − 1
Since a c − b = 3 b − 2 = 2 β ≡ 1 ( m o d 3 ) , β is even.
If β = 2 ,then b = 2 = a .False.
If β = 4 ,then b = 6 , c = 1 1 .
We are easy to verify ( 2 , 6 , 1 1 ) is satisfied.
If β ≥ 6 ,then b = 3 1 ( 2 β + 2 ) .Substituted it in b c − a and we have
9 × 2 α = 9 ( b c − a ) = 9 b ( 2 b − 1 ) − 1 8 = ( 3 b − 2 ) ( 6 b − 1 ) − 1 6 = 2 β ( 2 β + 1 + 5 ) − 1 6 ①
∵ α > β ≥ 6
∴ 2 7 ∣ 9 × 2 α ,but Eq.① only divisible by 2 4 and not divisible by 2 5 ,Paradoxical!
2° a ≥ 3
We have ( a + b ) ( c − 1 ) = 2 α + 2 β , ( b − a ) ( c + 1 ) = 2 α − 2 β .
∵one of c + 1 and c − 1 is not a multiple of 4
∴ 2 β − 1 ∣ ( a + b ) or 2 β − 1 ∣ ( b − a )
∵ 2 β = a c − b ≥ 3 c − b > 2 c
∴ b < c < 2 β − 1
∴ 0 < b − a < 2 β − 1
∴ 2 β − 1 ∣ ( b − a ) is false.
∴ 2 β ∣ ( a + b )
And a + b < 2 b < 2 β ,so a + b = 2 β − 1 .
∴ a c − b = 2 β = 2 ( a + b )
∴ a ( c − 2 ) = 3 b
If a ≥ 4 ,then b ≥ 5
∴ a ( c − 2 ) ≥ 4 ( c − 2 ) ≥ 4 ( b − 1 ) > 3 b .Paradoxical!
∴ a = 3 , c − 2 = b
∴ b = 2 β − 3 , c = 2 β − 1
∴ 2 γ = a b − c = 3 ( 2 β − 3 ) − ( 2 β − 1 ) = 2 β − 8
∴ β = 4 , b = 5 , c = 7
We are easy to verify ( 3 , 5 , 7 ) is satisfied.
In summary,there are 4 three-number sets satisfied.They are ( 2 , 2 , 2 ) , ( 2 , 2 , 3 ) , ( 2 , 6 , 1 1 ) , ( 3 , 5 , 7 )
I don't know whether IMO would encourage this or not, but i sat down and tried to find out all solutions. It turned out to be only 4. (2,2,2) (2,3,2) (3,5,7) (2,6,11).
Proof of (2,2,2). Let a=b=c
Therefore, a(a-1)=0(mod 2)
There's only 1 solution possible for this argument Hence one solution is (2,2,2)
I'll surely post solution for the rest three when I get them!
Please do post a proper solution.
Infact the IMO marking scheme does not allow for random solutions without the method used to solve the problem!( and the proof that these are the only solutions!)
Log in to reply
I don't know exactly how to do it. But I'll try.
Log in to reply
On the IMO, that solution would be scored as 0/7.
One thing you can do is to look at the solutions you have found, and try to find a "defining characteristic", which might suggest an approach. E.g. All of these numbers are small, is there a reason why we can bound all of these by say 20?
Log in to reply
@Calvin Lin – As a matter of fact you can prove that c is bound by 4.
@Calvin Lin – Sorry sir. Please could you suggest a good method??
@Calvin Lin – i think there are much better number theory problems then this , for instance , senior year baccalaureate exam 2015- maths sciences- in Morocco . If u'd like to see it i can send it to u to review it.
I think this problem's answer is incorrect--n should be 16 instead of 4.Because a&b&c is equivalent:)
For example (3,5,7) is satisfied,(7,5,3) also is satisfied.
@Shourya Pandey U were this year's Indian participant. Please help us out.
I think there is a problem in the commenting section here... @Calvin Lin -- the same comments are repeated in both "solutions" :-/
Log in to reply
Thanks. We are aware of it and will be fixing it.
How much time is allotted at IMO for such questions?
In my opinion not a very good problem, it was a routine bash. I'm not very good at number theory though, so I couldn't crack it without looking at the solution.
Log in to reply
Well the problem required too much bashing! But this was an interesting problem overall! If you start solving it you see so many ways to proceed yet all end in dead ends!