Cyclic Quadrilateral
The circle above has its center at point O , and arc D C is half the length of arc B C .
What is the measure of angle ϕ ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Posted to avoid the notifications. Hoping that it helps.
How can you say that DOB is the diameter? Its not said anywhere that DOB is a straight line??
Log in to reply
Please see the solution clearly, I have proved that angle DOB = 180 degrees. A question: Are you an RMO (IMO) aspirant?
Log in to reply
Oh I see , actually I didn't notice that!! Yes and who doesn't want to be but at the moment I am in class 12 so I am into board preparations!!
Log in to reply
@Nashita Rahman – Hmmm, nice. And you do not have any more chance left. Ok. I am in 9th. BOL for your 12th boards.
Log in to reply
@Vishwash Kumar Γξω – Thanks and All The Best to you for IMO !
Relevant wiki: Cyclic Quadrilaterals
Include the central point O of the circle. Since arc D C is half the length of arc B C , this shows that ∠ D O C = θ and ∠ C O B = 2 θ . Because point O lies on diagonal D B , we can see that ∠ D O C + ∠ C O B = 1 8 0 ∘ , where ∠ D O C = 6 0 ∘ . The reason why this must holds follows that ∠ C A B = 2 ∠ C O B . Then, ∠ C O B = 1 2 0 ∘ .
Being the central point of the circle, point O forms two isosceles triangles Δ D O C and Δ C O B . In that case,
- ∠ O C B = ∠ O B C = 3 0 ∘
- ∠ O D C = ∠ O C D = 6 0 ∘ , which implies Δ D O C is an equilateral triangle
Thus, since ∠ A C O = ∠ A C B − ∠ O C B = 1 5 ∘ the answer is ∠ A C D = ∠ D O C − ∠ A C O = 4 5 ∘
which follows Thale's theorem . We can see that the sum of each pair of opposite angles of the cyclic quadrilateral is 1 8 0 ∘ .
Note: Another way to approach this problem is to note that since B D is the diameter of the circle, one can note that two arc formed by B D have the same length. In that case, ∠ D C B = ∠ D A B = 9 0 ∘ . Thus, ∠ D C A = 4 5 ∘ .
Note: It is also possible to solve directly, using the fact that the quadrilateral is cyclic. Then, you are to solve ∠ D A C + ∠ C A D ∠ D A C + 6 0 = 7 5 = ∠ C A D + 4 5 So ∠ D A C = 3 0 ∘ and ∠ D C A = 4 5 ∘ .
How do you know O lies on DB?
Log in to reply
By "forces point O to be the center of the circle", are you constructing another point O' and proving that O=O'? It doesn't seem intuitive to me that DOB are collinear solely from BC=2DC.
Once you find out that angle DOC = 60degrees. Then you should directly write Angle DAC = 1/2 * ANGLE DOC = 1/2*60 = 30. And then the property that sum of any two opp. angles of a cyclic quadrilateral = 180. Straightaway, no need of some unnecessary constructions.
Log in to reply
Yes, that is true. Just showing the construction for fun. :)
Log in to reply
hahahah , When we know the answer to a particular angle hunt question, we can find many techniques to approach to the Solution, many constructions come in our mind. But when we don't know the answer neither one comes.
this is a good solution, but there is a better solution than this ,, in a cyclic quadrilateral , the sum of opposite angles equals 180 degrees . . .
isn't there a theorem that states "The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the circle" -by using this we can directly get angle COB as we know angle CAB
Log in to reply
Yes, it is, and you are right about the thought and idea. :)
As O lies on BD, BD is the diameter of the circle. And as C lies on the periphery of the circle, the triangle BCD is a right triangle, therefor the angle at C is 90° (Thale's theorem) and the searched angle is 90°-45°= 45°
How do we know O lies on BD?
Log in to reply
you do not need to know that O lies on BD, this is a cyclic quadrilateral ..angle A + angle C = 180 .. so to attack this problem, you must be familiar with the "intercepted arc and inscribed angle" ..
Log in to reply
This proof starts with the line, as O lies on BD. So for this proof we need the fact O lies on BD, I don't know why we can assume that. It doesn't matter if there is another way to prove it.
the question here is, how did you know that BCD is a right triangle?
Keep in mind: The measurement of an inscribed (vertex on the circle) is always 1/2 the measurement of the intercepted arc. So...
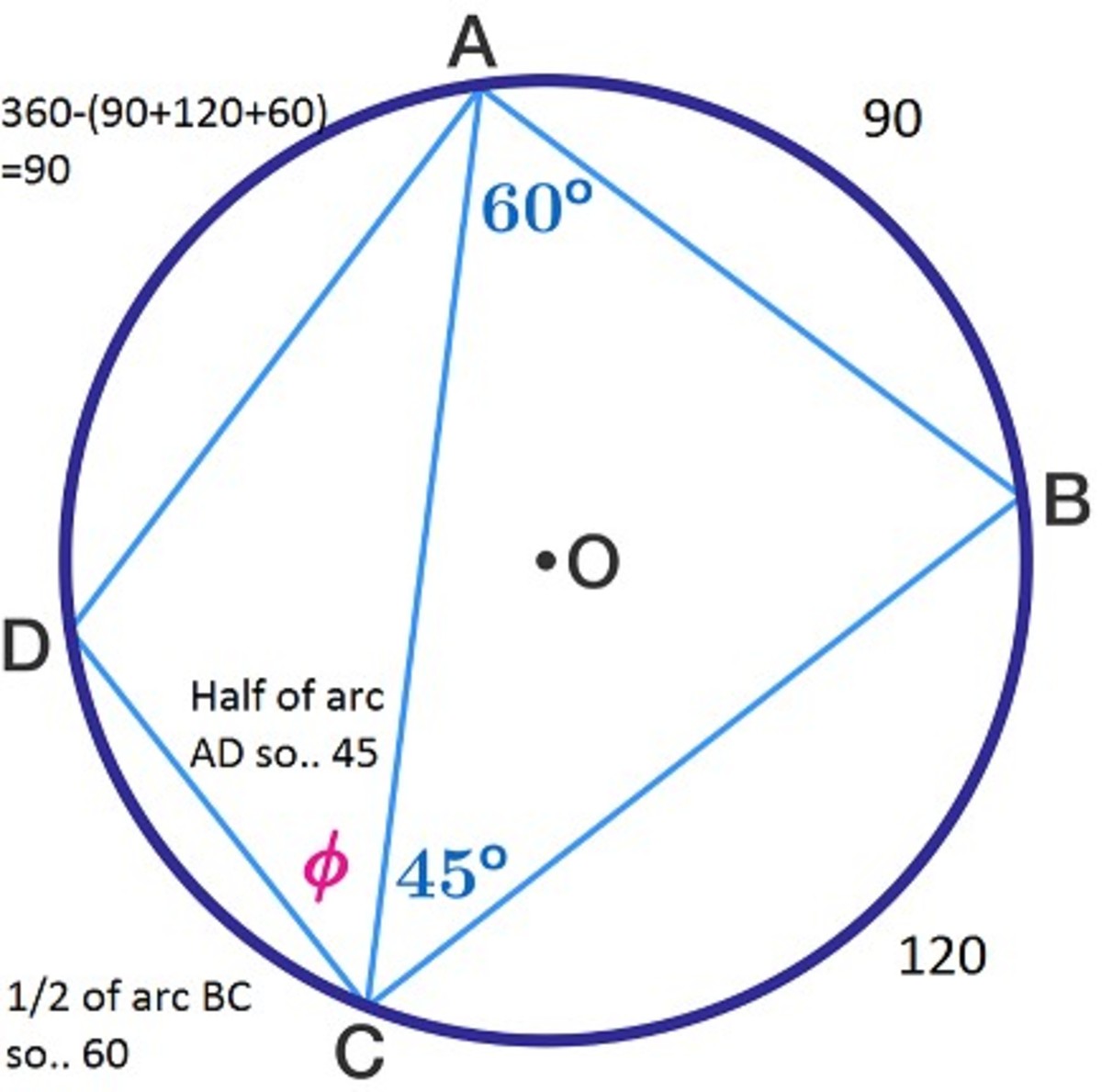
Best solution I did the same!
because < A C B = < A C D (Properties of a quadrilateral )so 45 degree