Cylinders don't jump and slip!
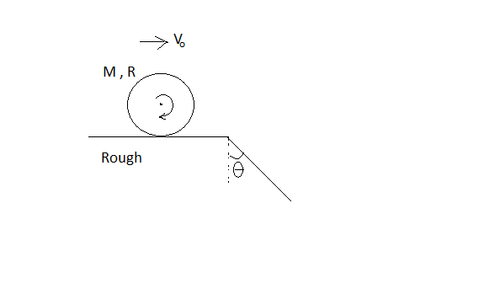An uniform solid cylinder of mass
M
and radius
R
rolls without slipping on horizontal passing into an inclined plane which makes an angle
θ
with the vertical as shown in figure.
Find the maximum value of the velocity v o which still permits the cylinder to roll onto the inclined plane section without a jump.
If it's maximum value can be expressed as
v o max = a g R ( b sin θ − c ) ,
then find the value of a + b + c .
Details and Assumptions
∙ There is sufficient friction on the entire surface (with coefficient of friction μ ).
∙ Here a , b , c are positive integers such that gcd ( a , b , c ) = 1 .
Source : I solved This question somewhere else ! And Liked it So I share this !
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I understood the problem ONLY after reading your solution. Congratulations. I think there is still a correction. It should be 3/4 not 2/4 ..(1) ??.
This is just an explanation of your steps.
The problem is to connect two concepts for the two position of the cylinder. In both the positions, the cylinder is at the EDGE.
Position A when the horizontal path is tangent to the cylinder, and B when the sloping path is tangent. When the cylinder moves from A to B, two things happen.
[1] Its PE reduces and its KE increases. [2] It turns round the corner from A to B where its CoG turns in a circular path with radius R. Thus the component of its weight, normal to the slope must at least be equal to the centrifugal force to avoid a jump.
[
1
]
C
o
G
f
a
l
l
b
y
R
(
1
−
C
o
s
α
)
.
F
o
r
C
o
G
v
e
l
o
c
i
t
y
v
a
n
d
r
o
l
l
i
n
g
w
i
t
h
o
u
t
s
l
i
p
p
i
n
g
ω
K
E
=
2
1
m
v
2
+
2
1
I
ω
2
.
B
u
t
I
=
2
1
m
R
2
.
∴
K
E
=
4
3
m
ω
2
.
∴
C
h
a
n
g
e
i
n
P
E
=
K
E
B
−
K
E
A
∴
m
g
∗
R
(
1
−
C
o
s
α
)
=
4
3
m
ω
B
2
−
4
3
m
ω
A
2
…
.
(
1
)
[
2
]
C
o
m
p
o
n
e
n
t
o
f
w
e
i
g
h
t
⊥
t
o
t
h
e
s
l
o
p
e
=
c
e
n
t
r
i
p
e
t
a
l
f
o
r
c
e
.
m
g
C
o
s
α
=
m
ω
A
2
∗
R
…
.
(
2
)
S
u
b
s
t
i
t
u
t
i
n
g
m
ω
A
2
∗
R
i
n
(
1
)
a
n
d
v
o
=
v
A
=
ω
A
∗
R
,
α
=
9
0
−
θ
,
w
e
g
e
t
t
h
e
g
i
v
e
n
v
a
l
u
e
.
.
Log in to reply
Since Rod has angular velocity so there is centripetal acceleration that will be provided by normal and 'mg' component !
And by Normal, I mean instant at which normal force is acted in direction making an angle α or you can say \90 - \(\theta ) .
Why can't we apply angular momentum conservation about ICR frame. I am getting different answer if I am trying to apply it.
Since the cylinder is rolling at the beginning, it has rolling kinetic energy. Shouldn't we subtract 2 1 I ω o 2 from equation (1)? Where ω o is inital angular velocity.
Log in to reply
You are right. Though Deepanshu Gupta has written o n l y − 2 1 m v o , h e i s u s i n g i n h i s c a l c u l a t i o n s − 2 1 m v o 2 − 2 1 I ω o 2 . S i n c e I = 2 1 m R 2 a n d v o = ω o ∗ R . . . . 2 1 m v o 2 + 2 1 I ω o 2 = 4 3 m v o 2 .
Sorry It was Typing Mistake in My solution ! But ok I edited That Accordingly!
@Aniket Sanghi @Prakhar Bindal
Why can't we conserve angular momentum abt the point abt which cylinder will perform pure rotation?
There is not impulsive torque abt that point.
Log in to reply
There is no impulse in the question!
Mg will apply torque! There is nothing like impulse in the question , mg gets sufficient time to give it's effect. So you can't apply angular momentum conservation .
Log in to reply
So we can't ignore torque due to mg since time period is sufficiently long.Thanks, got a new concept to learn that impulse due to finite forces can not always be ignored.
Thanks a lot!
yes of course mg will apply torque !
Let Cylinder is making an angle α with the vertical at any instant of time t=t .
Since there is no slipping so by Using conservation of energy ,In ICR frame ( Bottom most point )
m g R ( 1 − cos α ) = 2 1 I b o t t o m ω 2 − 2 1 I b o t t o m ω o 2 ( ∵ ω o R = v o ) m g R ( 1 − cos α ) = 4 3 m R 2 ω 2 − 4 3 m v o 2 . . . . . ( 1 ) .
Now writing equation of motion about normal line :
m g cos α − N = m ω 2 R . . . . . ( 2 ) .
Now Condition for Cylinder for Not Bouncing at any instant and rolls Purely is:
N ≥ 0 & α = 9 0 − θ . . . . . ( 3 ) .
Using all equation eliminate N , ω . we get :
v o ≤ 3 g R ( 7 sin θ − 4 ) v o , m a x = 3 g R ( 7 sin θ − 4 ) .