dancing HEXAGON
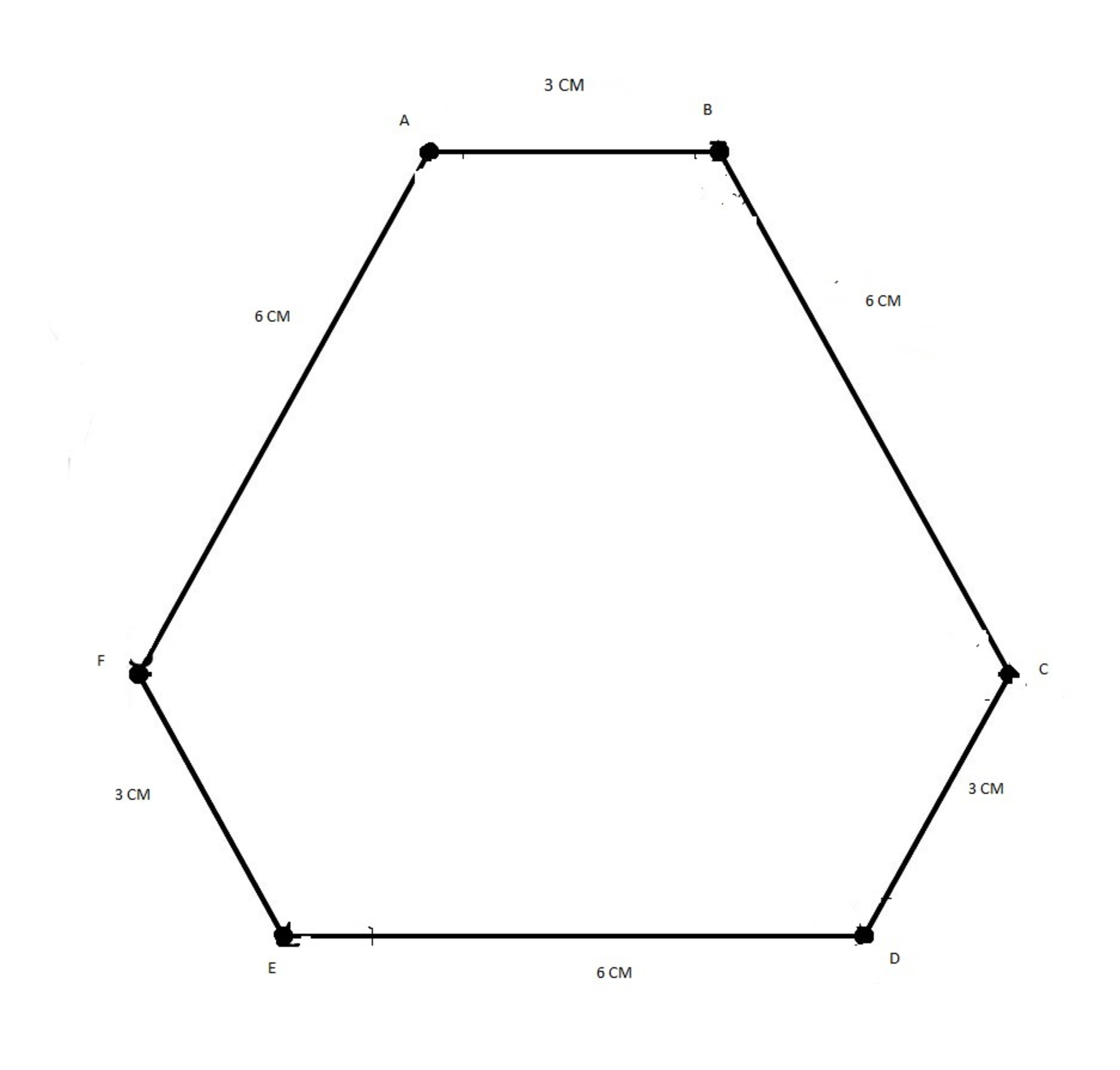
In a hexagon ABCDEF . Angle[AFE]=[FED]=[EDC]=[EDC]=[DCB]=[CBA]=[BAF]=120°. AB=CD=EF=3 and AF=ED=CB=6 find the area of this HEXAGON.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
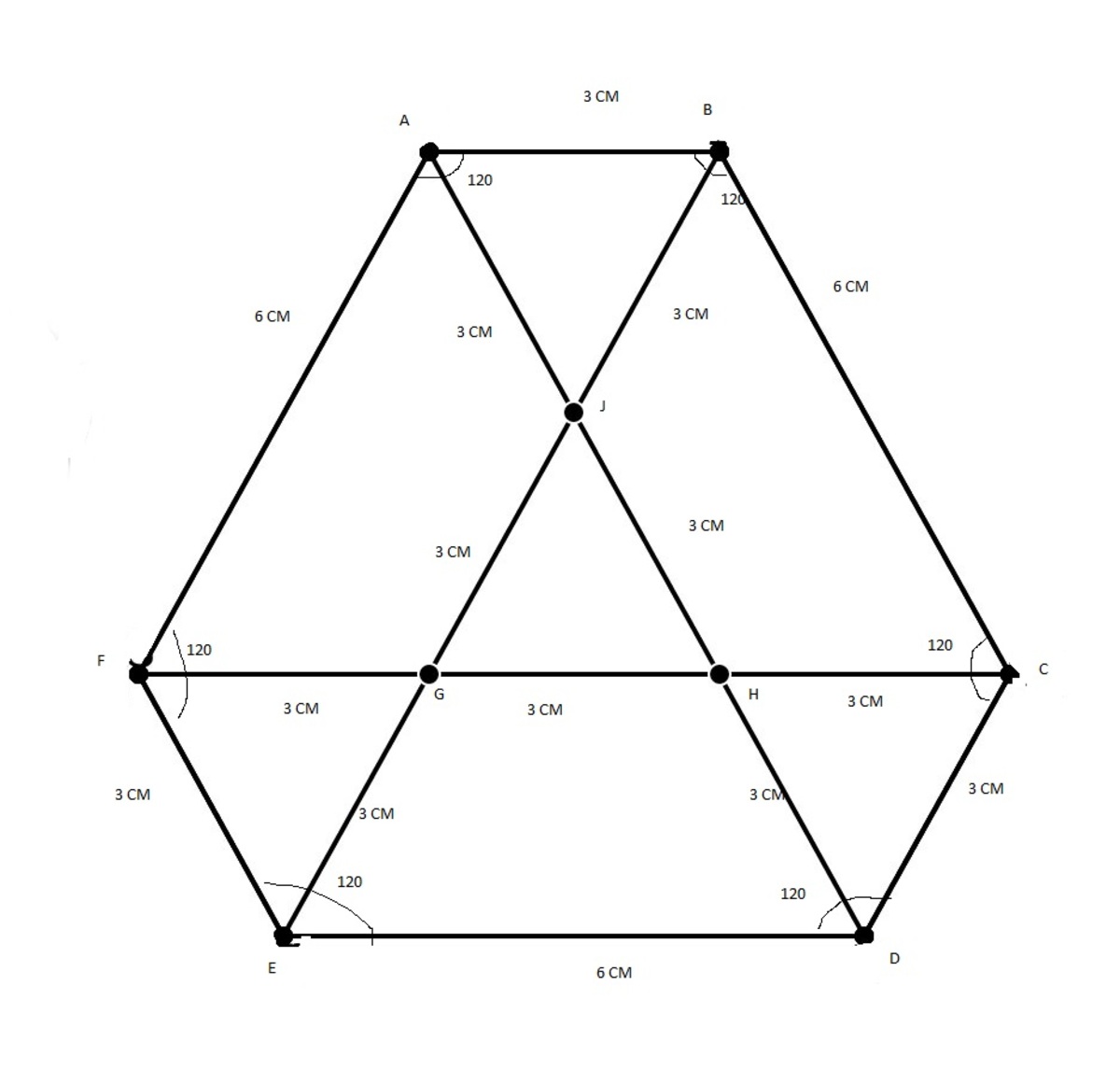
angle [ABC]=[BCD]=120 degree and AB=CD so angle [BAD]=[CDA]=60 degree so BC||AD in same way FC||ED so quadrilateral ABCH is a Parrallelogram so CH=AB=CD=HD=3 CM and angle [HCD]=[HDC]=[DHC]=60 degree. so triangle (ABJ) congurrent to (CHD)and(FGE) and all are equilateral triangle. (√3*(3)^2)/4=(1/2)(3)(Height) height =(3√3)/2
so area of trapezium ABCD= 1/2(6+9) (3√3)2 (45 √3)/4=11.25√3 ----------------1
AREA OF parallelogram AJEF=6*(3√3)/2 =(18√3)/2---------------------2
TRIANGLE JED is a equilateral triangle of each side of 6 CM
area of Triangle(JED)= (√3(36))/4= --------3
SUM OF 1,2AND3=AREA OF HEXAGON = 50.66
Watch out! In the picture in the problem description, you have side B C = 3 , but the solution uses B C = 6 .
Log in to reply
I am sorry Mr. Caleb Townsend I will correct my mistake!!!! :-)
Log in to reply
when yaar???? next year???
that's absolutely right... in question figure B C = 3 and in answer figure Lalit Jena has used B C = 6 but some how he has arrived at the correct solution!!!... silly jena...
Log in to reply
I am sorry Sarthak rath!! I will correct it in some years!!!
why don't you type this in latex as i did in mine?
Log in to reply
What is latex?
Log in to reply
look at the difference between my problems solution and yours... LaTeX is a high-quality typesetting system; it includes features designed for the production of technical and scientific documentation.
First, join F C to form trapezoids A B C F and C D E F . The area of a trapezoid is A = h × w , where h is the height and w is the length of the median, that is w = 2 1 ( b 1 + b 2 ) . Also, we aren't given the heights immediately, but we are given the angles in the trapezoids and slant lengths. So substitute h = l × sin θ , where l is the slant length.
The area of A B C F is A 1 = 6 sin ( 6 0 ∘ ) 2 3 + 9 = 1 8 3 The area of C D E F is A 2 = 3 sin ( 6 0 ∘ ) 2 6 + 9 = 4 5 4 3
So the area of hexagon A B C D E F is A = A 1 + A 2 = 1 1 7 4 3 ≈ 5 0 . 6 6