Dancing On a Parabola
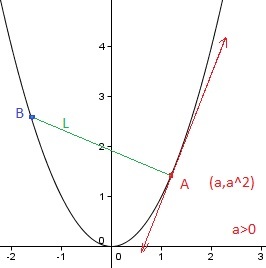
Suppose that two people, A and B, walk along the parabola y = x 2 in such a way that the line segment L between them is always perpendicular to the line tangent to the parabola at A's position ( a , a 2 ) with a > 0 . If B's position is ( b , b 2 ) , what value of b minimizes L ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You're absolutely right, Chew-Seong Cheong! Oops, I can't believe that I typed a 7 as the last digit! Forgive me, that was a typo! I can hardly believe that I typed it though, because I knew the square root of 2 was 1.4142135623731... I have memorized many surd roots (from sqrt(2) to sqrt(33) ), so I am embarrassed to have made the mistake, but glad you caught my error.
Log in to reply
Yes, earlier, there was someone commented the answer should be 2.0+. So I told him the answer was 2 . Since then he had deleted his comment. I was not complaining about your mistake.
For exam purpose, I memorized them too, when I was much younger. 2 = 1 . 4 1 4 , 3 = 1 . 7 3 2 , lo g 2 = 3 . 0 1 0 , lo g 3 = 4 . 7 7 1 . Now I have forgotten most of them.
Log in to reply
Cool! I memorize logs to 3 decimal places. I have memorized in increments of .1 from log(.1) to log(5). I am still trying to expand what I know in most areas such as cubes, square roots, logarithms, and fraction to decimal conversions, and multiplication facts, but I have the squares 1^2 to 100^2 memorized and can square 3 digit numbers and some 4 digit ones too. (always in 15 seconds or less mentally).
Log in to reply
@Jared Jones – What happens if the person who posts the problem is wrong? How quickly is the problem resolved?
Log in to reply
@Jared Jones – It gets fixed within 2-3 days after it's been reported. It's much faster if the problem creator helps us to fix the problem, or let us know what is wrong about it.
I've updated the answer to -1.414.
log(2) = .301, log(3)=.4771 (just the decimal point in the wrong place)
link - I use WolframAlpha
would you like to explain how do you get a = 1/sqrt(2), because I get this .
Log in to reply
Sorry, there are typos with d a d L 2 = . . . . . I have amended it.
@Chew-Seong: in the dL^2/da line there is the square missing on the first (4a^2+1) term.
The answer is − 2 = − 1 . 4 1 4 2 1 4 .
The gradient of the parabola at point A is: m P = d x d y = 2 x = 2 a
Therefore, the gradient of line segment L which is perpendicular to the parabola at point A is: m L = − m P 1 = − 2 a 1
⇒ a − b a 2 − b 2 = a + b = − 2 a 1 ⇒ b = − a − 2 a 1
⇒ L 2 = ( a 2 − b 2 ) 2 + ( a − b ) 2 = ( − 2 a a − b ) 2 + ( a − b ) 2 = ( a − b ) 2 ( 4 a 2 1 + 1 ) = ( 2 a + 2 a 1 ) 2 ( 4 a 2 1 + 1 ) = 1 6 a 4 ( 4 a 2 + 1 ) 3
To find the minimum L ,
d a d L 2 = 1 6 a 5 3 ( 4 a 2 + 1 ) 2 ( 8 a 2 ) − 4 ( 4 a 2 + 1 ) 3
When L is minimum, 2 4 a 2 − 1 6 a 2 − 4 = 0 ⇒ a 2 = 2 1 ⇒ a = 2 1
When b = − 2 1 − 2 2 = − 2 1 − 2 1 = − 2