Day 11: Escape the Field
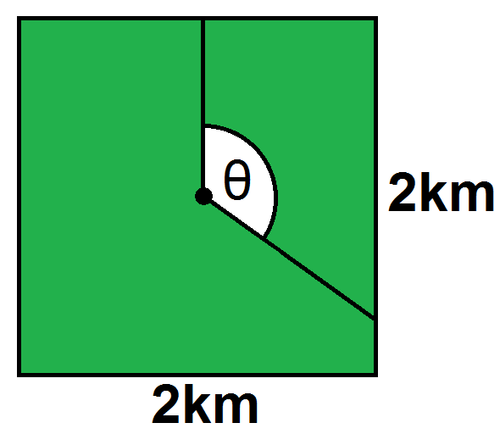 I am stuck in the centre of a square field of side-length 2km. I randomly pick a bearing on my compass then walk in that direction until I reach the edge of the field.
I am stuck in the centre of a square field of side-length 2km. I randomly pick a bearing on my compass then walk in that direction until I reach the edge of the field.
In metres, find the expected distance that I travel and round your answer to the nearest metre.
This problem is part of the set Advent Calendar 2014 .
The answer is 1122.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Why cant the answer be ∫ 0 1 1 + x 2 d x ? Just wondering, because both ways are considering the average of an infinite cases, and yet they are different in the "Compactness" of the cases which gives different answers. Is there a mathematical way to address this problem?
Log in to reply
There's a note on ambiguity in determining probability of an event if random experiment is not clearly stated. Link
This is something that I had thought of also; it really is very strange. It turns out that using that method gives a different answer, even though it seems logically correct! That is why I had to specify that the bearing was chosen randomly.
Log in to reply
This is my attempt to explain it:
 hi
hi
As you can see, for the ∫ 0 1 1 + x 2 d x , it is more concentrated at the corners.
I don't think there is any mathematical explanation for this. Sorry for the bad graphics
Log in to reply
@Julian Poon – When you integrate with respect to x, you are assuming that the x-coordinate is chosen uniformly. In fact, in the graph on the left, you can easily see that \delta x is the same for each ray where it interesects the boundary. The problem specified that it was the "direction" (i.e., \theta ) that was chosen uniformly (which is correctly illustrated by the graph on the right. Therefore we must integrate the distances with respect to \theta .
When it comes to continuous probabilities, the "density" of your free variable can drastically change the outcome, as you have discovered.
Log in to reply
@Tyler Hanna – Tyler Hanna, very nice explanation! :D I intuitively felt what you've so articulately explained.
@Tyler Hanna – Yeah. The image I posted doesn't really show that does it?
Log in to reply
@Julian Poon – No, no, it shows it perfectly. I was just explaining the math behind why the graphs look the way they do, and why they give different answers.
@Julian Poon – That is very nice. Thank you :)
I would rather take ln tan [Pi/ 4 + (Pi/ 4)/ 2] to evaluate.
Given that for angle θ the distance is 1 / cos ( θ ) then for a distance x we have that the angle is F ( x ) = arccos ( 1 / x ) . The probability that he travels of a distance between [a,b] is equal to 4 ( F ( b ) − F ( a ) ) / π . Therefore f ( x ) = F ′ ( x ) 4 / π is the distribution of probability. The expectaction can be calculated with the following formula ∫ 1 2 f ( x ) x d x where 1 and 2 are the minimum and maximum distance he can travel.
So f ( x ) = π x x 2 − 1 4 and ∫ 1 2 π x 2 − 1 4 d x = 1 . 1 2 2 2 . Therefore the answer in meters is 1222.
The integral is calculated by replacing z = x 2 − 1 to have ∫ π z 2 + 1 4 d z which is equal to sinh − 1 ( z ) 4 / π = ln ( z + z 2 + 1 ) 4 / π . which results in ln ( x + x 2 − 1 ) 4 / π .
Three lines up from the bottom the "1222" should be "1122".
We only need to consider the case where 0 ≤ θ < 4 π , as the other cases are identical to this one.
So what we want is: ( 4 π ) ∫ 0 4 π sec x d x = ( 4 π ) [ ln ( sec x + tan x ) ] 0 4 π = 1 . 1 2 2 1 . . .
But our answer needs to be in metres, therefore our answer is 1 1 2 2 as required.