19 of 100: Crazy Pizza Cuts
What is the maximum number of pieces you can divide a circular pizza into with 4 cuts?
All cuts must be distinct straight lines from one point on the edge of the pizza to another point on the edge of the pizza, and you may not move the pizza slices.
Assume the pizza is flat (so the cuts all must be from above). Try experimenting with 2 cuts and 3 cuts before going on to 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Who the hell cuts pizza like that?!!
How did you get from Pn+1 = Pn + n + 1 to the general equation for Pn? I don't understand.
Log in to reply
yes i'm stuck at the same point as well
Write the recurrence relation as P n = P n − 1 + n . Here, it can be said that the + n part is the difference between two consecutive terms. Since P 0 = 1 , it follows that
P n = P 0 + k = 1 ∑ n k = 1 + 2 n ( n + 1 ) = 2 n 2 + n + 2
The summation here can be thought as a cumulative sum of differences. :)
Hey the answer could have been 14 if we slice to 7 pieces with 3 cuts and the 4th cut slicing the thickness of pizza in half ( parallel to top face) but the author said cuts must touch the edge so 11 is the maximum we can attain
Log in to reply
"All cuts must be distinct straight lines from one point on the edge of the pizza to another point on the edge of the pizza." - Brilliant Staff (Is it?)
It can be cut into 14 pieces consider pizza is 3D.
There is a difference between the number of cuts that can be made and the position of the pepperonis. There is no guaurantee that one of the cuts will not slice through a pepperoni. The diagram is not compatible with the pizza diadram- Ed Gray
I understand this now, I think, but do you mean "induction", instead of "introduction"?
Question can you cut a pizza like that with equal area slices?
It could be 12
Log in to reply
12 is impossible.
Log in to reply
It's impossible, but can you prove it? I don't think she is convinced if you just say so.
Log in to reply
@Steven Jim – I proved it in the above solution.
Log in to reply
@Khang Nguyen Thanh – Oh yeah. I misread a little bit. Sorry.
By the way, it should be "by induction".
12 is possible when it is 3D
Log in to reply
@Oliver Zhou – I don't think it's 3D.
Besides, if ever it is 3D, then the answer must be 14 instead.
If you say that 12 is possible, give me a drawing showing how.
"All cuts must be distinct straight lines from one point on the edge of the pizza to another point on the edge of the pizza." - Brilliant Staff (Is it?)
It is possible
Each line can only intersect any other line once at most. Each intersection closes the boundary of a new 'piece' - thus, if drawing the optimal solution, each new line should be drawn so it intersects every other line once at distinct positions. The nth line will create n new pieces when drawn: one for every intersection with the n-1 other lines, and one for reaching the circumference.
0 lines: 1 piece
1 line: 1 + 1 = 2 pieces
2 lines: 2 + 2 = 4 pieces
3 lines: 4 + 3 = 7 pieces
4 lines: 7 + 4 = 11 pieces
n lines: 1 + (1 + 2 + 3 + 4 + ... + n) = 1+ n(n+1)/2
It is also noteworthy that this progression of numbers (2, 4, 7, 11, etc.) is the sequence of triangular numbers (1, 3, 6, 10, etc.) shifted in the positive direction by 1.
Triangular numbers are the numbers formed from adding the first n whole numbers beginning with 1, where n is a positive whole number. For instance, when n = 3, you find 1 + 2 + 3 = 6. This is why 6 is a triangular number.
It is only natural that each term of the "intersection numbers" (2, 4, 7, 11, etc.) is one more than its corresponding triangular number. This is because with the addition of the nth line, you create n new pieces of the pizza, and you obviously begin with 1 whole piece. So the addition is: 1 + 1 + 2 + 3 + 4...
Anyways, I just thought that was cool. :D
EDIT: I just saw the last line of Joe's post. "...1+ n(n+1)/2." (n(n+1)/2 is the formula for finding the sum of the first n whole numbers.) Explained my entire post in 10 characters...haha XD
I figured out the "correct" solution but kept thinking, a pizza has thickness, so by cutting it parallel to the surface, it could be divided into 8 pieces with 3 cuts and 15 pieces with 4 cuts... you should have stated more clearly that the cuts must be perpendicular to the surface.
No need to cut "horizontally" to get sixteen slices...
First cut the pizza in half. Pick up one half and place it on top of the other half. Now make a second cut, halving both halves. Pick up two quarters and make a stack 4 quarters high. Cut again to get eight pieces. Finally stack up all eight eighths and make one final cut giving sixteen pieces.
Log in to reply
This is exactly what I thought. I found the question misleading.
Log in to reply
@Adam Goodkind Actually, to do this, you would cut from the edge to the middle of the pizza, which is not really the edge of the pizza, only the edge of the figure you have created. Also, thinking realistically, that would be a lot of pizza sauce being squirted out of our cuts. When the pizza is flat on the table/plate/platter, it doesn't lose as much delicious sauce and toppings (Although, the pepperoni can go, I am a vegetarian)
Log in to reply
@Ayush Kumar – then you are saying that all the other solutions are wrong, because they go from the edge, not the center.
Thats what I thought, but somehow the answer is 11, not 16?!?!
If you're going to ignore the problem description to allow stacking, why not allow folding? :-)
No - it was stated really obviously what this question meant and what you were trying to achieve. Sorry guys, but these are the sort of silly arguments I would expect from my Y5's (9-10yo's) By Y6 I'd expect less niggling and more rigorous thinking.
Log in to reply
I note that the question has now been re-written to exclude this solution to the original, incomplete statement of the problem.
Log in to reply
The advantage of doing a puzzle like this in a classroom is you can re-write it on the spot if your English wasn't clear enough first time - however much the kids grumble!!
The question did say each cut must go from one edge to another edge, which doesn't really fit with cutting horizontally.
Brother think this practically I have never seen a pizza with thickness sufficient enough to cut parallel and it would also be difficult to cut parallel as all the layers of cheese and toppings are loosely bound between layers
Log in to reply
Nothing is impossible.
Log in to reply
:-D ya bro but I dont think any one would like to eat that
Log in to reply
@Ayush Sharma – We have to solve the problem buddy , we aren't here to eat pizza. Please visit nearby pizzahut, food panda or Domino's for that purpose.
LOL 😅😂😊
"All cuts must be distinct straight lines from one point on the edge of the pizza to another point on the edge of the pizza." - Brilliant Staff (Is it?)
Log in to reply
If it has to be the original edges, we could stack the pieces in opposite directions. For example, after the first cut, the bottom piece would have the straight edge on top, with the curved edge on the bottom. The other piece(s) would be rotated 180°. Then a cut from the middle of the bottom edge to the middle of the top edge is still a cut from an original edge to an original edge.
If we're stacking the pizzas, like above, then wouldn't the cuts be from edge to edge, even if those are not the original edges?
Log in to reply
We can't stack, of course. I agree though that the problem isn't fully stated.
Same here.
when they ask to draw a straight line from one edge on the pizza to another they refer to it perpendicular to the surface, because otherwise you would be embracing every single edge of the pizza if you cut it parallel to the surface, and wouldn't be possible to just cut from one edge to another, you would be intersecting every single one...
It could be 12
Log in to reply
If you say that 12 is possible, give me a drawing showing how.
"All cuts must be distinct straight lines from one point on the edge of the pizza to another point on the edge of the pizza." - Brilliant Staff (Is it?)
Besides the approach mentioned by others, here is another way to look at it. We know, from Euler's characteristic equation, V − E + F = 2 where V is the number of Vertices , E is the number of edges and F is the number of Faces. Now, to maximize the number of faces, we need to maximize V and also minimize E .
Consider, if we had only 2 lines, whatever configuration we use, both lines will intersect at max 1 point and thus one new vertex will be created.
For 2 lines, V = 5 , E = 8 and F = 4 + 1 which satisfies 5 − 8 + 5 = 2
Here, the number of faces equal to 4 + 1 because we need to consider the area outside the pizza as 1.
If we had 3 lines, we can draw the third line such that either it passes through the intersection of other two lines or cut both lines.We get maximum faces when the line cuts the other two.
For 3 lines, V = 9 , E = 1 5 and F = 7 + 1 which satisfies 9 − 1 5 + 8 = 2
Similarly in case of 4 lines, we can draw the line such that it cuts the maximum number of lines thus creating more vertices and it results in maximizing number of Faces.
For 4 lines, V = 1 4 , E = 2 4 and F = 1 1 + 1 which satisfies 1 4 − 2 4 + 1 2 = 2
The formula gives you exact result instantaneously but this helps in understanding the idea behind the solution. :-)
Links
This is one of the possible answers...
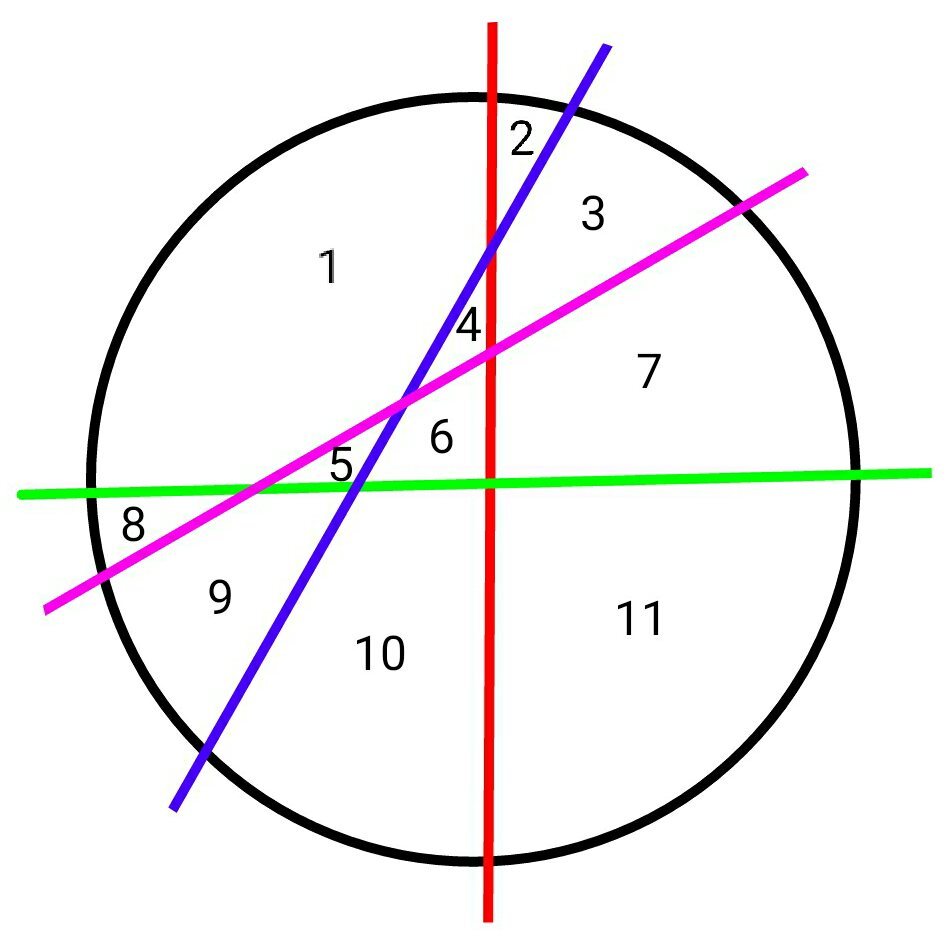
nice solution! The trick of this problem is to draw a straight line which crosses all the existing straight lines at separate crossing points to maximize the number of pieces to divide the pizza into.
Note that a complete solution should also justify why 12 is impossible.
Log in to reply
12 is possible
Log in to reply
If you say that 12 is possible, give me a drawing showing how.
"All cuts must be distinct straight lines from one point on the edge of the pizza to another point on the edge of the pizza." - Brilliant Staff (Is it?)
To make more slices, there would have to be another intersection of cuts inside the circle. But each line already intersects the other three inside the circle.
The cool thing is that the same idea generalises to 3D and further, with which you could e.g. also solve the following problem proposed in Germany's Bundeswettbewerb Mathematik in 2016:
Each side face of a dodecahedron lies in a uniquely determined plane. Those planes cut the space in a finite number of disjoint regions. Find the number of such regions.
Good thinking. If this were a cake(with thickness) , some answers above were 12. But those wouldn't be right either as the plane cut could cross more than 1 plane also. I haven't figured the answer yet but it would be more than 12.
Question should be more clear. It is also missing that cuts should be straight lines not curves.

This is what the pizza looks like after slicing it...
To maximize the number of pieces, each line drawn must intersect every other line, and no three lines should intersect at one point. This is because the more intersections there are, there must be more pieces, as there will be more regions in between intersections. Following these rules, we can draw a circle and draw four lines. Counting the segments there are, we get the answer 1 1 .
If you make one cut, then the pizza will be cut into 2. If you make two cuts, then the pizza will be cut into 4. If you make three cuts, then the pizza will be cut into 7. 2 +2 = 4 4+3=7. The pattern is: +2 +3 +4. So 7 plus four equals to 11.
For the first cut, you slice it into 2 pieces.
For the second cut, you want try to have this cut intersecting with all the previous cuts (There's 1). So you have increased 2 pieces.
For the third cut, you want to try to have this cut intersecting with all the previous cuts too (There's 2 of them). 3 pieces increased.
...
In general, the maximum pieces you can get after n slices is
2 + ( 2 + 3 + 4 + . . . + n ) = 1 + 2 n ( n + 1 ) = 2 n 2 + n + 2
When n = 4 , you get 1 1 of them.
Why is difficulty "Might Draw Blood"? It's so easy.
n-th cut can't cross more than n-1 cut lines. It cuts one more piece, so no more than n. Therefore n-th cut increases the number of pieces by up to n. And so on...
The problem is requesting the maximum number of regions a plane can be divided by 4 lines. In order to achieve this maximum, there can't be a pair of parallel lines (otherwise rotating one of them forms at least another region and this would contradict the maximality of the number of regions).
There are n over 2 intersection points 2 n ( n − 1 ) and each of them corresponds to a region. Lines, of course, don't stop at intersection points, and define other (non closed) region: to account for them we can imagine drawing a straight line which gets n cuts from the n lines, dividing it in n + 1 parts, with each of them corresponding to a region. So there are 2 n 2 + n + 2 regions, which could be written beautifully using binomials.
We can generalise the problem to "In how many parts can a space be cut by n planes at maximum"? I will now sketch the solution, which is analogous and based on the previous one (spoiler warning!): the intersection of three planes defines a point, which can be associated bijectively to a region. Then, the n planes will cut an auxiliary plane in the maximum number of regions a plane can be cut by n lines, as the intersection between two planes is a line (which will meet other lines on that plane).
The central polygonal numbers, also known as the Lazy Caterer's Sequence, helps give the maximum number of pieces a circle can be cut into with a certain number of straight cuts.
We can begin to find a formula for this by solving a recurrence relation for the total number of pieces after n cuts as follows:
We start with f ( n ) = n + f ( n − 1 ) . Expansion of this function gives us f ( n ) = n + ( n − 1 ) + f ( n − 2 ) , which expands into f ( n ) = n + ( n − 1 ) + ( n − 2 ) + f ( n − 3 ) , which expands repeatedly in the same format until we reach the resulting expanded function where the last f ( n ) has been reduced to 0 . Therefore, we have f ( n ) = n + ( n − 1 ) + ( n − 2 ) + ( n − 3 ) + . . . + 3 + 2 + 1 + f ( 0 ) . We know that f ( 0 ) = 1 , so 1 is added in the final simplification of the completely expanded function above. Therefore, we have the function f ( n ) = ( 1 + 2 + 3 + 4 + 5 + . . . + ( n − 1 ) + n ) + 1 , which simplifies to f ( n ) = 2 n ( n + 1 ) + 1 , and then simplifies to f ( n ) = 2 n 2 + n + 2 , which is the Lazy Caterer's Formula.
Plugging in n = 4 into the Lazy Caterer's Formula, we get 1 1 as our final answer.
One interesting thing to note is the sequence formed for the Lazy Caterer method. The sequence is as follows:
1 , 2 , 4 , 7 , 1 1 , 1 6 , 2 2 , 2 9 , 3 7 , 4 6 , 5 6 , . . .
Notice anything? If we look closely at the sequence above, we can see that it follows a pattern such that for each of the triangular numbers 0 , 1 , 3 , 6 , 1 0 , 1 5 , 2 1 , 2 8 , 3 6 , 4 5 , 5 5 , . . . we add 1 . This is no coincidence, however! Looking back at our method to find the Lazy Caterer's Formula and it's application to the problem, we can note that the formula for the n th triangular number, 2 n ( n + 1 ) , was added to the result of the function f ( 0 ) = 1 .
- When you have 0 cuts, that means you have 1 whole pizza. With 1 cut it becomes 2 slices and with 2 cuts it becomes it 4 slices. So we start to notice a pattern. With each cut, there is ( x ) more slices. So if you continue the pattern you get 11 cuts. You can generalize this problem into ( x 2 +x+2)/2 for x cuts
We can easily find a recursion method f(n)=n+f(n-1), then we count f(3)=7 and we find f(4)=4+f(3)=3+7=11
Well i didn't know any formula for this, so I simply started making figure and all cases in my mind here is what i got:
1. Cutting with 1 line - 2 parts
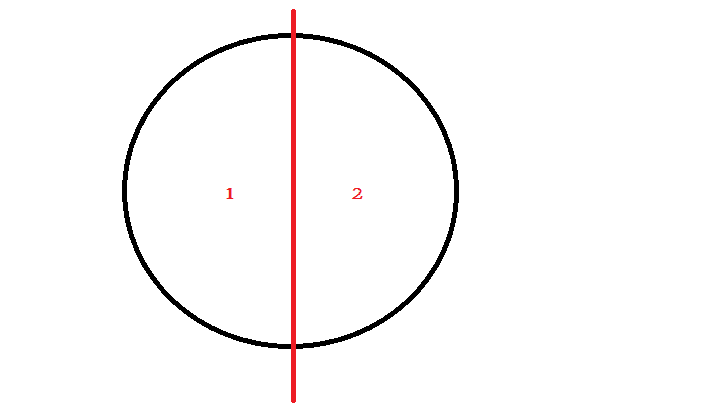 2. Cutting with 2 lines:
a. when both have 1 common point - 3 parts
2. Cutting with 2 lines:
a. when both have 1 common point - 3 parts
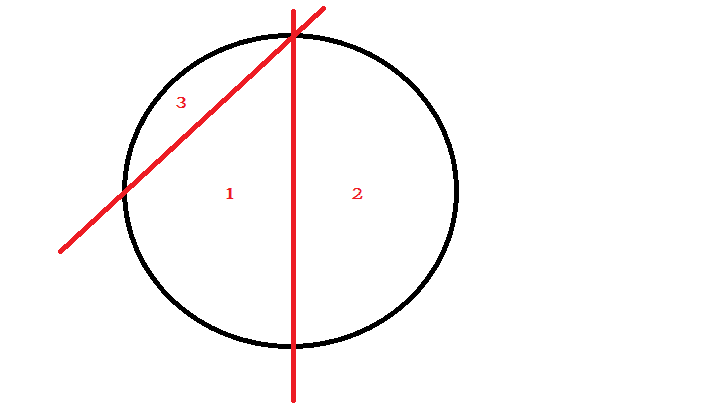
b. when both have no common point - 4 parts
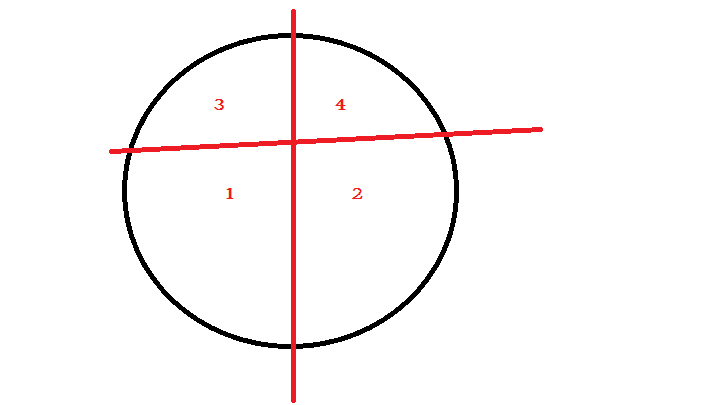
-
Cutting with 3 lines:
a. when all 3 have 1 common point - 4 parts
b. when all 3 have 1 common point with 1 line at circumference - 4 parts
c. when 2 of them have a common point and 3 is not intersecting any of them - 4 parts
d. when 2 of them have a common point and 3 is intersecting any 1 of them - 5 parts
e. when all 3 lines make a triangle with 2 vertex on circumference and 1 within circle - 5 parts
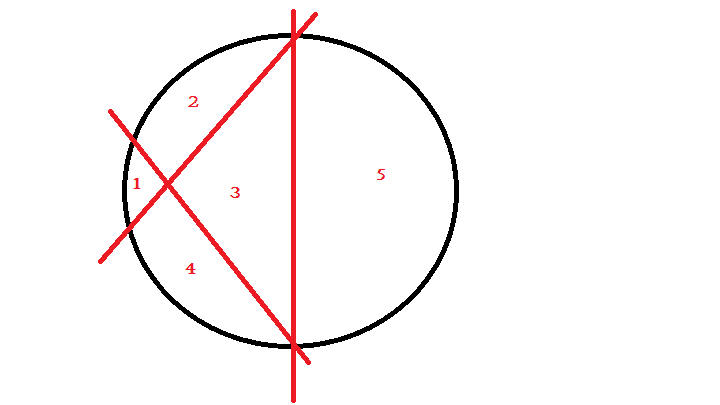
f. when all 3 lines make a triangle with 1 vertex on circumference and 2 within circle - 6 parts
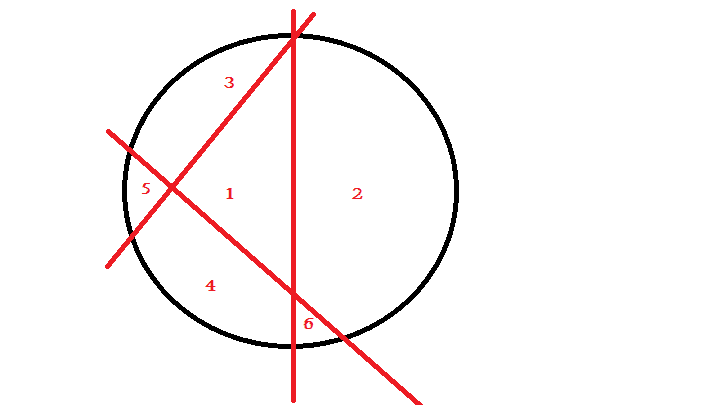
g. when all 3 lines make a triangle with all 3 vertex within circle - 7 parts
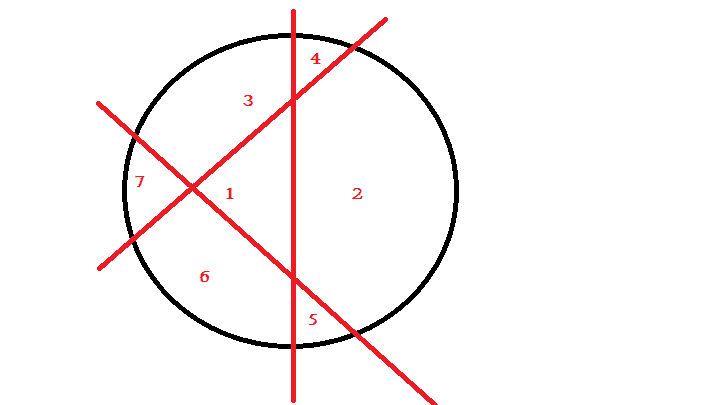
-
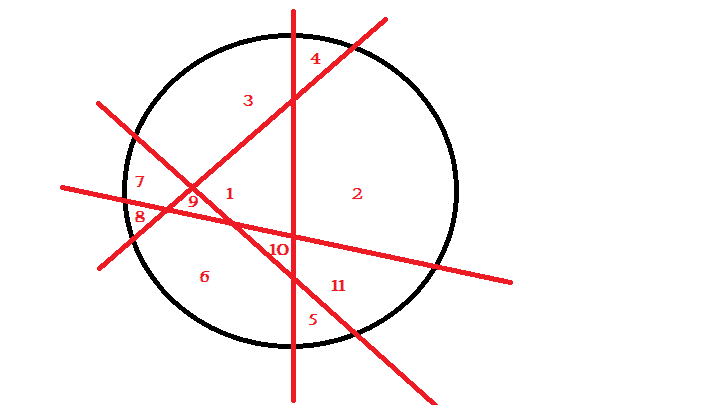
By the above methods we can see that number of parts is directly proportional to intersections within circle, so 4th line should be placed in such a way in fig 3(g) that it enhances number of parts toits fullest, so here it is -
11 parts
f ( n ) = 2 1 ( n 2 + n + 2 ) is the formula for cutting a circular pie with n cuts.
Thus, f ( 4 ) = 2 1 ( 4 2 + 4 + 2 ) = 1 1
those formula blasts...
Log in to reply
I am famous for writing small solutions :) We can prove it by induction thou.
We can prove a general result by induction:
Let P n is the maximum number of pieces you can divide a circular pizza into with n cuts.
With 1 cut, a pizza will be divided in to 2 parts, so P 1 = 2 .
Each new line intersects other n lines in one point and divides each previous region of space into two regions. Therefore each new line adds at most new n + 1 regions and so we have: P n + 1 = P n + n + 1
We can see that P n = 2 n 2 + n + 2 and hence P 4 = 1 1 .
This is a possible answer for n = 4 .