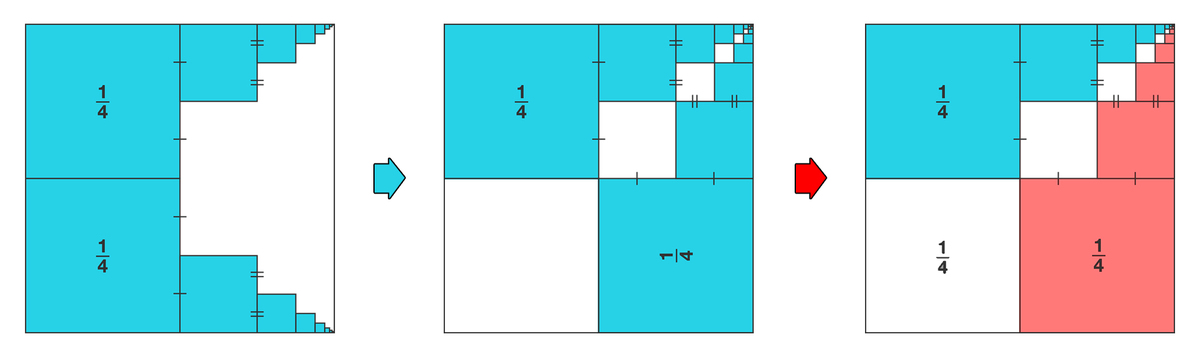
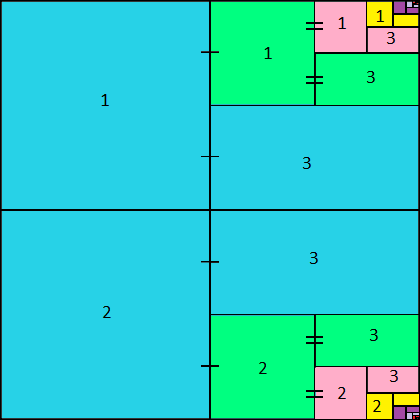
22 of 100: Squishing Squares
The left half of a square is occupied by two smaller blue squares as shown, each a quarter the area of the original large square.
To the right of both squares there is a succession of blue squares, each one connecting to the midpoint of the previous square as shown.
When this process is repeated many times, approximately how much of the original large square is shaded blue?
It all adds up more neatly than you might expect. Think about the symmetry of this situation.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
42 solutions
How should I interpret the image?
Log in to reply
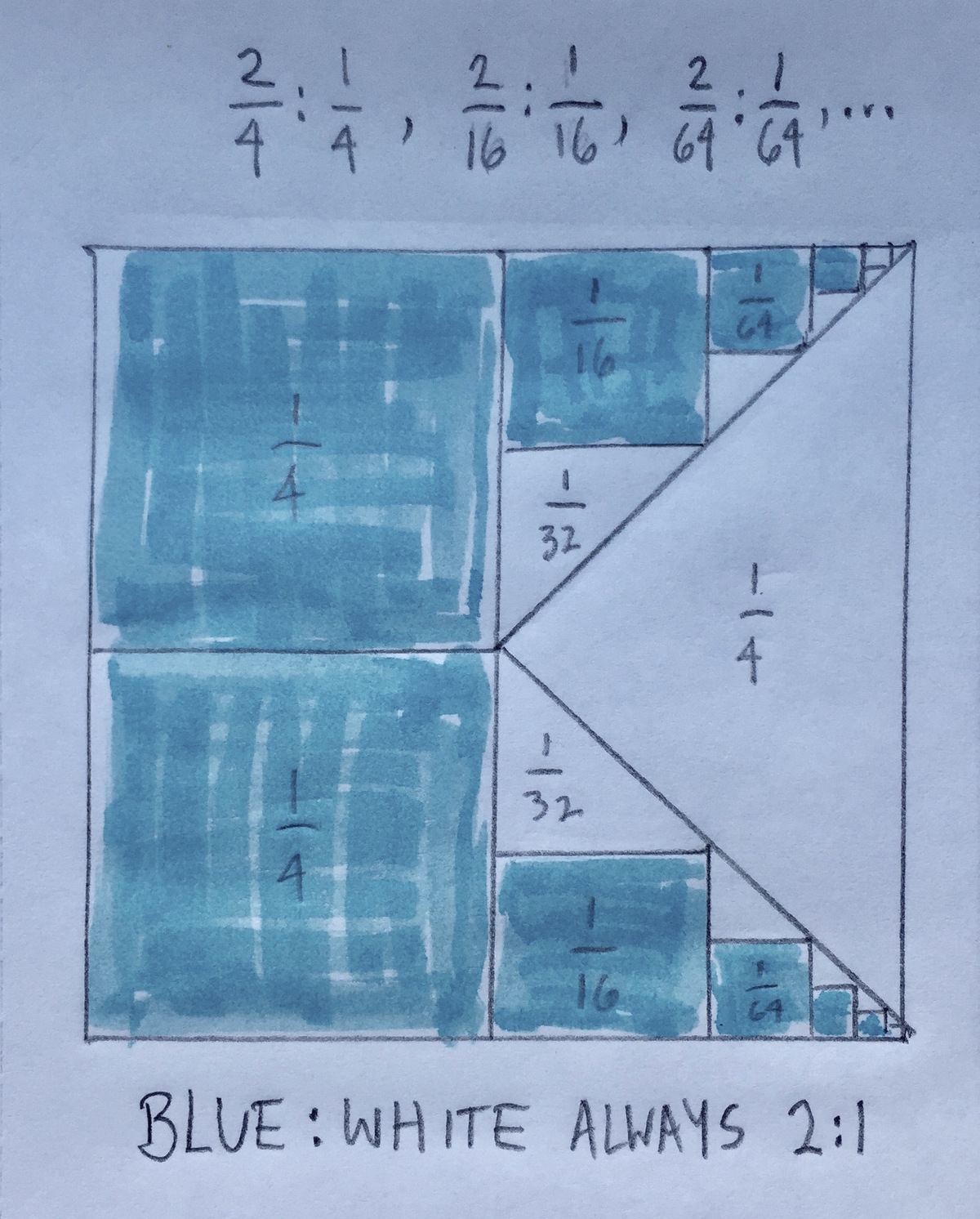
Visualize (or sketch) a horizontal line cutting each square in half. Then the colors reveal that for every 2 stacked rectangles that are included, there is 1 equal rectangle to the right that is excluded.
Log in to reply
Thanks for the explanations guys, I get it now.
Each square (each color) appears three times.
Log in to reply
The smaller ones appear four times
Log in to reply
@Virgil Mepsted – Two of them are rectangles that add up to a square.
After using the series method, I thought of this method as a proof that what I had done was correct. To help visualize it better, I like the idea of sliding all the squares directly down to stack them. Now at each iteration there are 4 regions to look at, the left 2 are blue, the bottom right has a bunch of smaller squares and the top right is empty. Therefore, 2/3 regions is blue. Very cool way to see it.
Your coloring suggests that the area shaded blue is 6/8=3/4 which doesn't correspond to the right answer!
Log in to reply
I have showed that there are three equal areas!
Log in to reply
Okay. I meant to point out the fact that the area shaded blue in your answer doesn't correspond to the area shaded blue in the problem. Otherwise good answer :)
Log in to reply
@Med Nait – Aha, you are right, the picture is confusing! I am too lazy to color it again :))
You still don't make sense
Let's first look at the top half of the diagram.
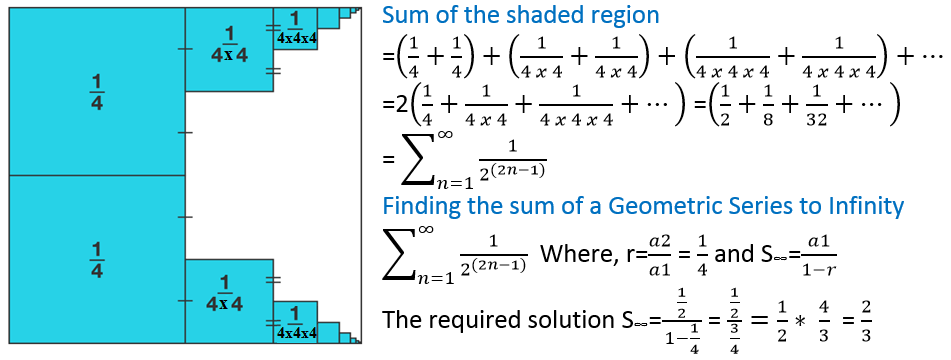
The second square is like the first square, but scaled down to 2 1 × 2 1 = 4 1 of its area. The third square is like the second square, also scaled down to 4 1 of its area. And so on. Therefore second square + third square + ⋯ = 4 1 ( first square + second square + third square + … ) . Or, all top squares − first square = 4 1 ( all top squares ) . Therefore, if we write A for the total area of all squares on top, we get A − 4 1 = 4 1 A . Solve this: A − 4 1 A = 4 1 , 4 3 A = 4 1 , 3 A = 1 , A = 3 1 . This is the total area of the squares on top. The bottom contributes the same amount, so we find a total of 2 / 3 .
Best explanation
Let s = the side length of the largest square and its area is s 2 . The first 2 blue squares have side length exactly one half of the biggest square so their areas are both 4 1 s 2 , and we can see all the succeeding blue squares have areas which are one fourth of the square immediately preceding them since they have one half of its side length.
The total area shaded in blue is therefore ( 4 1 s 2 + 1 6 1 s 2 + 6 4 1 s 2 + 2 5 6 1 s 2 ......) * 2 . As the number of blue squares goes to infinity, the summation in the parenthesis becomes an infinite geometric series . The series converges since its common ratio is 4 1 which is between -1 and 1. It sums up to 1 − r a where a is the first term( 4 1 s 2 in this case) and r is the common ratio which is 4 1 .
So the total area shaded blue is approximately ( 4 1 s 2 /(1- 4 1 )) * 2 = 3 2 s 2 and its fraction of the largest square is = 2 / 3
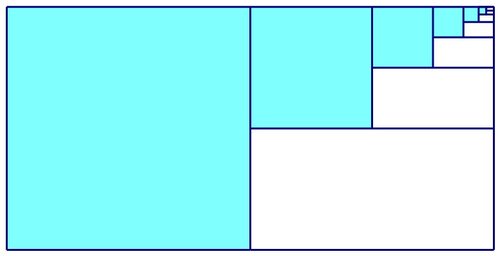 We have a pictorial question, so let's have a pictorial proof! Look at the top half of the original square. Each white rectangle is half the area of the blue square immediately to its left. Thus there is twice as much blue as white, and so the overall proportion of blue is
3
2
.
We have a pictorial question, so let's have a pictorial proof! Look at the top half of the original square. Each white rectangle is half the area of the blue square immediately to its left. Thus there is twice as much blue as white, and so the overall proportion of blue is
3
2
.
This is my favored solution I saw here. It's very simple and clear to understand.
This is my favourite solution too. Beautifully simple and elegant :) .
Makes sense to me.
- I used a super quick, non-mathematical way to get the correct answer using simple logic. Just looking at the puzzle it's clear that the blue area is more than 1/2 but less then 3/4 of the original square. There is only one answer option in between these i.e. 2/3
Exactly how I solved it :) an open answer text box should have been better
Me three
If this was in a situation where the priority is to get a correct answer quickly, maybe for a SAT-type test, then I think this method (using the process of elimination) is the best
Log in to reply
I think the priority in solving any problem is to get the correct answer quickly
Log in to reply
Is that so? Maybe during tests, but sometimes the process is more important than the result.
Let me borrow the words by @Mark Hennings , from the comment under his own solution to the problem "Roundabout" :
"...solving problems under time constraints is not the ultimate aim of mathematics. If you are in an exam, where someone has checked that there is a single answer, then a shortcut will often get you to the answer. However, that shortcut has not taught you why that answer is unique. Personally, I find the "why" much more interesting than the simple answer."
You should take a look at the solution itself as well, if you haven't already. It goes one step ahead to prove that the answer would remain the same even if the diagram was misleading.
( https://brilliant.org/100day/day24/)
Isn't it simply... more interesting than just finding the correct choice?
Log in to reply
@Jubayer Matin – I totally agree that it gives more satisfaction and entertainment to actually solve a problem with proof. But giving obviously wrong options as choices kills the joy, because I know the correct choice as soon as I read the whole problem just by automatically/intuitively eliminating all the others. I don't even have control over that, my mind does it to me. Creators must keep this in mind if they think it is important to make solvers actually prove the solution. If they don't, it's alright to leave it this way.
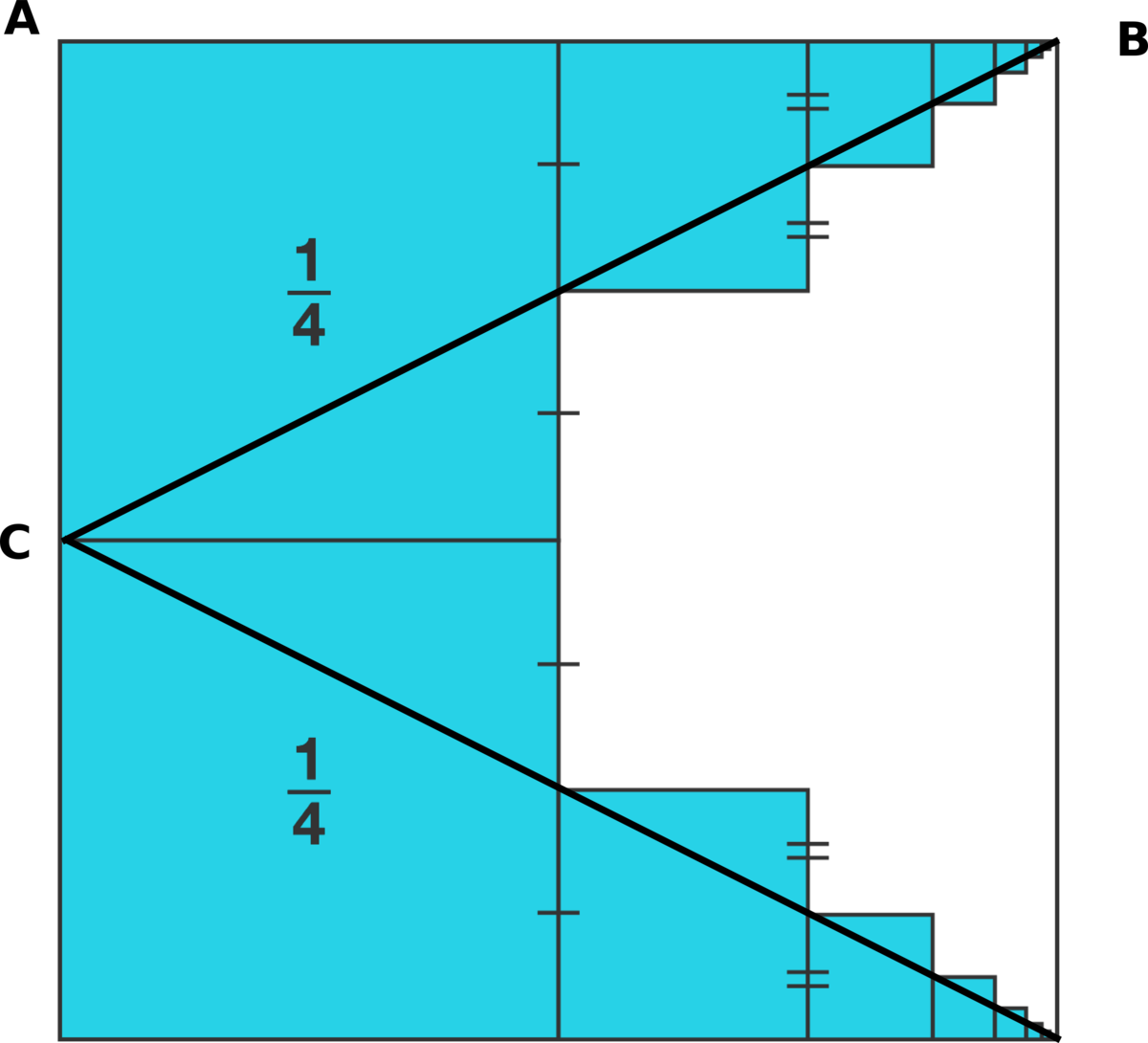 The area
A
of ABC is
4
1
. (BC) splits equally each blue square such that the blue area under (BC) represents
4
1
of the whole blue area (on the upper half of the square).
Thus,
A
is
4
3
of the total area, which is then
3
1
The area
A
of ABC is
4
1
. (BC) splits equally each blue square such that the blue area under (BC) represents
4
1
of the whole blue area (on the upper half of the square).
Thus,
A
is
4
3
of the total area, which is then
3
1
I put in the diagonal line shown and am only considering the squares that lie above that diagonal line.
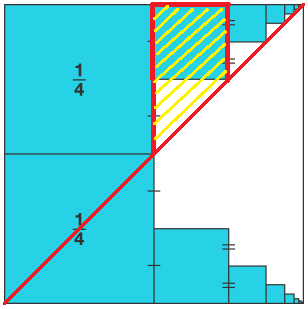
I am seeing this parts above the line as being a collection of trapezia. Each trapezium (one of which is shaded yellow) is a square stuck to a right-angled isosceles triangle. This shows that within each trapezium, 2/3 is covered by the square.
The blue squares in the top half are therefore 2/3 of the area of half the big square. This means the blue is, altogether, 2/3 of the area of the big square.
I used the same method :)
We can consider one half of the figure (either the top or the bottom half) for convenience. Let the side length of the square be x .
Therefore the side length of each of the following squares would decrease by a factor of 2 1 .
Now considering the sum of their respective areas, we have:
Total shaded area of one half of the square = ( 2 x ) 2 + ( 4 x ) 2 + ( 8 x ) 2 + ⋯ = ( 4 x 2 ) + ( 1 6 x 2 ) + ( 6 4 x 2 ) + ⋯ = x 2 . 1 − 4 1 4 1 Total shaded area of one half of the square = 3 x 2 ( Using the formula for infinite sum of a G.P. )
Therefore the total area shaded in the complete square = 2 . 3 x 2
Fraction of area of the square shaded = x 2 3 2 x 2 = 3 2
This is a dumb solution, but maybe useful as a reminder of test-taking strategy.
It's more than 1/2 because the original two squares on the left are already 1/2, plus there's all the other squares.
It's less than 3/4 because if you let all the upper-right-quadrant squares slide down, they will not fill the lower-right quadrant.
Thus the answer to the multiple-choice question must be 2/3.
Let's focus on the top-half.
The area of the first blue shaded square is
4
1
.
In each step we add a square with an area of
4
1
of the previous square.
Therefore, the area of the
n
-th square is given by the geometric series
a
n
with first term
a
1
=
4
1
and common ratio
r
=
4
1
a
n
=
a
1
r
n
−
1
a
n
=
4
1
(
4
1
)
n
−
1
a
n
=
4
n
1
The sum of the
k
first terms of
a
n
is given by:
∑
n
=
1
k
a
n
=
a
1
r
−
1
r
k
−
1
∑
n
=
1
k
a
n
=
4
1
4
1
−
1
4
k
1
−
1
∑
n
=
1
k
a
n
=
3
1
−
4
k
1
To find the total area of the top half of the blue squares we want to sum
a
n
from
n
=
1
to
∞
. So, if
S
n
is that area then:
S
n
=
lim
k
→
∞
∑
n
=
1
k
a
n
=
lim
n
→
∞
3
1
−
4
k
1
=
3
1
−
0
=
3
1
Since
S
n
is the area of the top half blue squares, the total blue area is:
2
S
n
=
3
2
The first two squares, taken together, occupy half the total area. Then, the next two take up a quarter of the remaining half - an eighth of the total. This pattern continues, the next ones taking up 1/32 of the total and so on.
If S(n) is the sum of these areas, then 1/4 S(n) turns each term into the next one. Subtracting 1/4 S(n) from S(n) gives 3/4 S(n) = 1/2, and so S(n) = 2/3.
If the blue area is x, then 4x = x + 2, because 4 times each bit less than 1/4 is the same as the next bigger bit, and 4 * 1/4 * 2 = 2. This means 3x = 2, so x = 2/3.
Let the area of original square be a , and S be the area of portion of original square which is shaded blue , then S = 4 1 a + 4 1 a + 1 6 1 a + 1 6 1 a + 6 4 1 a + 6 4 1 a + . . .
= ( 4 1 + 4 1 + 1 6 1 + 1 6 1 + 6 4 1 + 6 4 1 + . . . ) a
= ( 2 1 + 2 3 1 + 2 5 1 + . . . ) a
= ( i = 0 ∑ ∞ 2 2 n + 1 1 ) a
The series in above is infinite geometric series with common ration r = 4 1 . Hence,
S = ( 1 − 4 1 2 1 ) a
S = 3 2 a
Hence answer is 3 2
We have: 2 (1/4) + 2 (1/16) + 2*(1/64)... = 1/2 + 1/(2^3) + 1/(2^5) + 1/2^7... = 2/3
Considering the top half, and noting that the area of the blue squares on the bottom half is of course equal to the areas at the top half. Call the SUM of the areas of the blue squares S. So 1/2 x S = (1/2)^2 + (1/4)^2 + (1/8)^2 + (1/16)^2 + ....... So S = 2 x [(1/2)^2 + (1/4)^2 + (1/8)^2 + (1/16)^2 + .......-------(1) Multiply both sides by 1/4 Hence 1/4xS = 2 x [ (1/4)^2 + (1/8)^2 + (1/16)^2 + .......] -----------(2) Take (2) from (1) gives 3/4xS = 2 x (1/2)^2 as all other numbers in equation 1 are cancelled out in equation 2. So S = 2/3 Regards, David
It is clearly more than 1/2 as the 2x 1/4s are shaded It is less than 3/4 as the 3rd qtr is not complete So 2/3 is the only viable answer
simply use geometric progression and series
The distance between 1/2 and 2/3 is 1/6. The next step in the Progression of the area of the blue squares is 2 ∗ ( 2 2 ) 1 which is smaller than 6 1
The difference between the is 2 ∗ ( 2 2 ) ∗ 3 1 , which is bigger than the next area in the Progression, 2 ∗ ( 2 4 ) 1 and so on. The difference is always bigger than the next step in the Progression, the reason is, that the Ratio with 3 multiplied with a power n of two must be Extended by 2^2, the other Ratio with 3. So the difference between the infinite sum has after the Extension always a numerator of 4 and the Ratio of the new added area a numerator of 3, it's always smaller but converges.
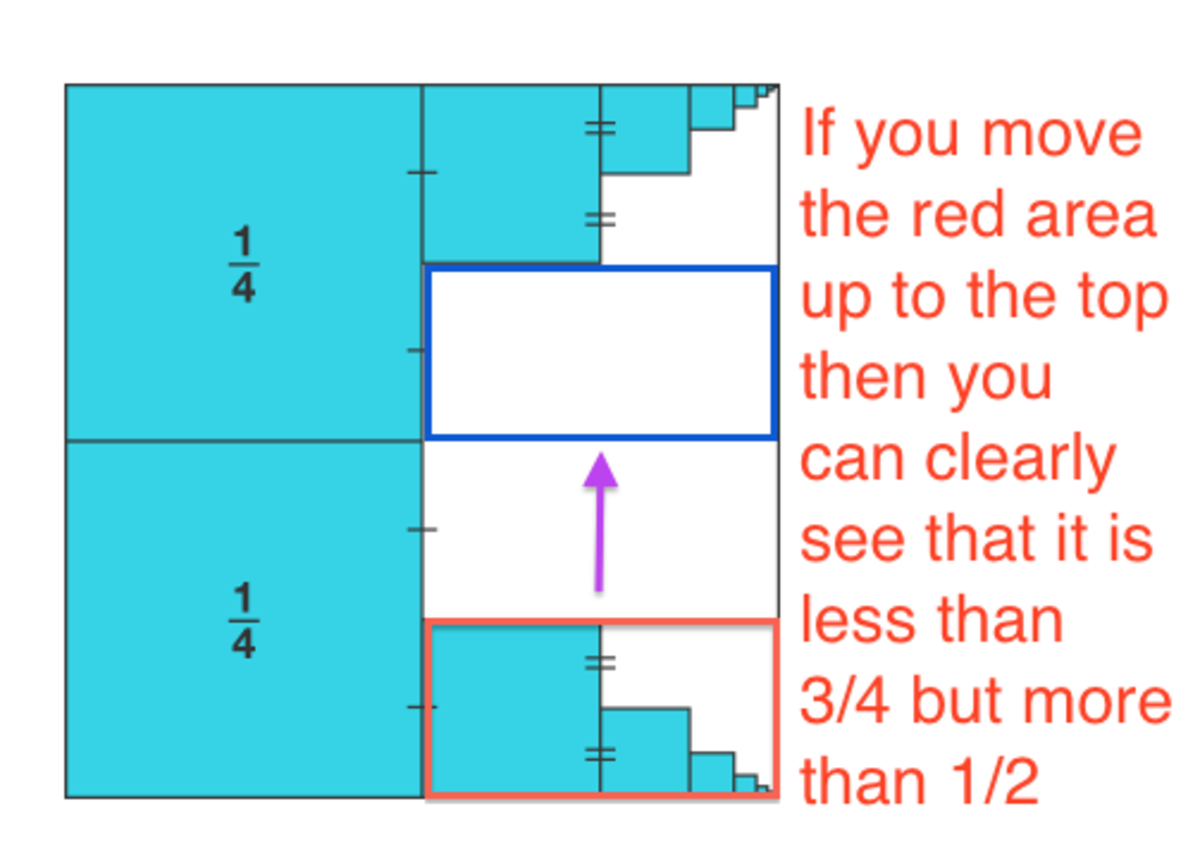
The way I did this super quick was to look at it and to imagine moving the lower squares up and saw it would be less than
4
3
but more than
2
1
Choose the best. Guess. When you add the 'blue' rectangles, it should equal 2/3.
2 times ( 4 1 + 4 2 1 + ...... + 4 7 1 ) = 3 2
Let the area of the main square be LATEX S the sum of all the blue squares above :
LATEX S = 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + ⋯ + 4 m 1 ( I )
LATEX Let’s multiply this sum S by 4 1 1 :
LATEX 4 1 S = 4 2 1 + 4 3 1 + 4 4 1 + 4 5 1 + ⋯ + 4 m + 1 1 ( I I )
LATEX Let’s substract ( I I ) and ( I )
LATEX: We can then simplify and we get :
LATEX S − 4 1 S = 4 1 − 4 m + 1 1
LATEX S × ( 1 − 4 1 ) = 4 1 1 − 4 m + 1 1
LATEX S × ( 4 4 − 4 1 ) = 4 1 − 4 m + 1 1
LATEX S × ( 4 3 ) = 4 1 × ( 1 − 4 m 1 )
LATEX S = 3 4 × 4 1 × ( 1 − 4 m 1 )
LATEX S = 3 1 × ( 1 − 4 m 1 )
As we know, LATEX lim m → ∞ 4 m 1 = 0
Then LATEX S = 3 1
As we have the 2 same blue areas, the answer is :
LATEX S = 2 × 3 1 = 3 2
Loop hole: Has to be grater than 1/2 and lesser than 3/4. Only 2/3 fits!
It can be represented by a geometric series a/(1-r), where a is the first term, and r is the number you multiply to get from one number to the next. a = 1/2 (1/4 + 1/4), and r = 1/4.
Therefore, (1/2)/(1-1/4) = (1/2)/(3/4) = 1/2 * 4/3 = 2/3
of the choices given, you can see from the picture that 3/4 and 5/6 are impossible, as is 1/2. so the answer must be 2/3.
It is a very simple question of GP ( Geometric Progression )
Let A = Area of whole square
Then Area covered by Blue Region will be
Series = 2 × [ ( 4 1 ) + ( 4 1 ) 2 + ( 4 1 ) 3 + ( 4 1 ) 4 + … ] × A
Sum of GP for infinite terms = 1 − r a
a = 4 1
r = 4 1
Sum = 2 × 1 − 4 1 4 1
= 2 × 4 3 4 1
= 2 × 4 1 × 3 4
Area covered by Blue Region = 3 2 × A
It is evident that the filled area is more than 1/2 because there are already two 1/4 squares. It is also evident that the area filled is less that 3/4 as that would occur only if half of the space not occupied by the 1/4 squares was filled. (The fact that it is less then this is most apparent by visualizing a diagonal line from the center of the original square to, for example, the top right corner and realizing that the areas filled by 1/16+1/64+1/256... squares make up less than half of single 1/4 square.)
Therefore, the answer must be between 1/2 and 3/4, which leaves only 2/3.
I did mine pictorially as well, no math required. If you slide all the lower shapes UP next to their counterparts you can see that an entire 1/4 of the square is open. Next look at just the 1/4 with the small squares and you can see that you are missing a full 1/16 square. Following this pattern, for every size shape, you will have two blue versions and miss one white version. Therefore 2 out of 3 are blue... so 2/3 of the area is blue.
If this was a multiple-choice test, you can visually illuminate all three answers within a few seconds. There is obviously more than half, and after using my method you can see there's less than 3/4 immediately. So the only possible answer is 2/3 of the choices
(Sorry no pic to go with it, if someone understands and adds one I would appreciate it.)
The sequence continues in the pattern 2(1/4)+2(1/8)+2(1/32).... This simplifies to 1/2+1/8+1/32 A pattern is found: 1/(2^(2x-1)) -If we use sigma notation for the first one hundred terms we have: SUM (1/(2^(2x-1))) x=1; 100 This is equal to 2/3
The blue areas are the sum of two geometric series with common ratio 1/4. The sum of the base series 1 + 1/4 + 1/16 + 1/64 + .... is given by 1/ (1-(1/4)) = 4/3. In this case the sum starts with the second term. After subtracting 1 for the missing first term, the sum is 1/3. Since there are two such series composing the squares of the blue area, the total blue area is 2/3. Since the area of the given square is 1, that is also the proportion covered.
No math here, just logic based upon the given possible answers:
Imagine all of the smaller squares in the top right quadrant fell exactly straight down and landing on the squares below leaving no spaces between. They, with the squares which were already there, would not fill that quadrant. Therefore the answer has to be less than 3/4.
The two squares on the left half of the original large square occupy 1/2 of it, and since there is some quantity of blue squares on the right half, the answer must be larger than 1/2. The only answer satisfying both parameters is 2/3.
By process of elimination the blue region is obviously bigger than 2 1 and smaller than 4 3 . As 6 5 > 4 3 ( 1 2 1 0 > 1 2 9 ) that leaves only 3 2 as a possible answer.
Each successive square is 1/2 the sidelength of the previous square, so it should be 1/4 the area of the previous square. Using an infinite geometric series, we can figure out the sum of the areas of all the squares on one half of the big square. This is 1 − 4 3 4 1 = 3 1 . Since there are two of these such blue square sequences, we multiply this by two to get 3 2 .
This is going to be ugly, but my personal challenge is to pass a certain test later this summer. I failed last time by running out of time - too much thinking - so what I need to do is find answers quickly in multiple choice form.
Thus, I added up the fist few terms.
1/2 + 1/4 + 1/32 + 1/128
Punched them into a calculator, and noticed the result is pretty darned close to 2/3, which is one of the choices.
Infinite sum of a series = a1/(1-r). For one set of blue squares, (1/4)/(1-1/4) = 1/(4-1) = 1/3. Multiply that by 2 = 2/3.
Each side is getting smaller by a geometric progression with the first term and the ratio as 4 1 ,
Thus, the sum is S= 1 − 4 1 4 1 = 3 1 multiplied by 2 gives 3 2
When we add up the two 1/4 squares, we get 1/2. Since more is shaded than just those two squares, we know at least 1/2 of the box is shaded. When we look at the white space, we can see (from the congruent line marks) that we could fit a 1/4 square in that space. Since there's more white space than what would be taken up by that 1/4 square, we know that the white space has an area greater than 1/4, which means the shaded area has to be less than 3/4.
Of the four answers, by process of elimination, only 2/3 is greater than 1/2 and less than 3/4.
The sum of the areas of the upper sequence of blue squares form a geometric sequence with first term a = 1/4 and common ratio r = 1/4. Thus, the sum of the areas of the upper sequence of blue squares is a/(1 - r) = 1/3. By symmetry, the lower sequence has the same area as the upper sequence. Therefore, the total area of the blue squares is 2/3.
It is nearly the same as one of my problems: Inspired by a Brilliant problem