3 of 100: A Pythagorean Spiral
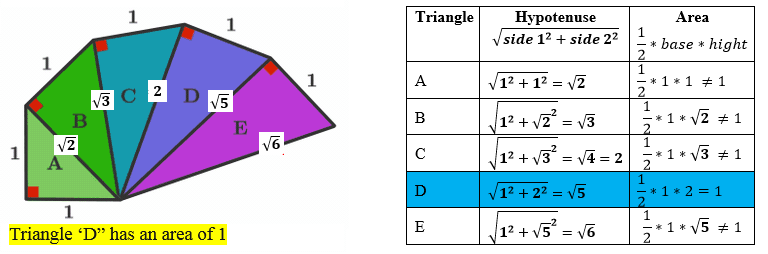
Which triangle has an area of 1?
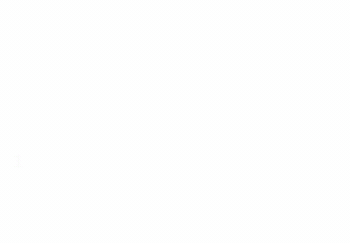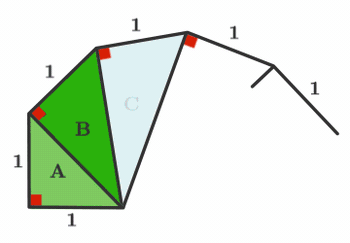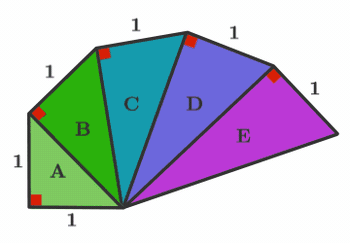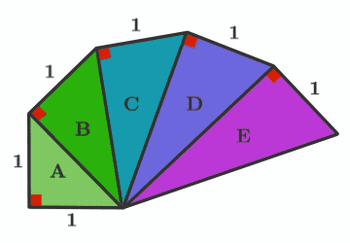
If you ever need to construct a line that is, in theory, N units long, now you know one way to do it! Can you design another construction technique?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
27 solutions
what is that construction technique
Log in to reply
Use of 45-45-90 triangle: the first 1 has sides 1, so hypothenusa is sqrt(2). From there it's Pythagoras.
Since triangle A has hypotenuse sqrt(2), each consecutive triangle after a would be sqrt(2+n) where n is the nth position after triangle A.
The hypotenuse we are looking for is sqrt(4) because (1) it is an integer and (2) the area of the next triangle would equal (sqrt(4) * 1) / 2.
We see that triangle C has the hypotenuse of sqrt(4), but we are looking for the triangle with a side of sqrt(4), so the answer is D.
what do you think about another technique to form a line of length N .
@Ashish Siva @Siva Budaraju @Joel Kang @Richard Desper @sam dave
Log in to reply
What do you mean?
Log in to reply
@Siva Budaraju if you see complete question till the end you'll find a note giving info about difficulty level Just beside that this bonus question is given
Log in to reply
@Abhijit Dixit – You could take a number line, draw a right triangle on it of sides 1, √N. Then the hypotenuse will be √(N+1). Use a compass to rotate the hypotenuse onto the number line. Voila, you have a line of √(N+1) units. Now repeat the process to get √(N+2), √(N+3), ..... units.
Log in to reply
@Siva Budaraju – Yup... And this is what they have used here. I was just stressing on the word ""ANOTHER CONSTRUCTION TECHNIQUE"
Log in to reply
@Abhijit Dixit – No, here they used right triangles that shared sides. My technique is similar but not the same.
Depending on the value of N, you could find a pair of squares a^2, b^2 such that a^2 + b^2 = N. If there's no pair, there might be a triple. That would probably be faster than using (N-1) triangles.
Log in to reply
yes sir that's a different approach. well would that be true for all n?
Note that the hypotenuses of each right triangle slowly increase as you go around the spiral (called the Spiral of Theodorus). As given by the other solutions, the base length of D is 4 = 2 , so the area of D is 1. My solution is more focused on constructing a line segment of N .
Consider a line segment A B of length N + 1 . Let C be a point on A B such that A C = 1 and B C = N . Let O be the midpoint of A B . Consider a circle centred at O passing through A and B . Let this intersect the perpendicular from C to A B at D and E . We have C D = C E = N .
brilliant soln
Log in to reply
computerisation
i also aim for making a line segment of desired quantity
Please explain the line ''Let this intersect the perpendicular from C to AB at D and E.'' I am unable to understand.
Log in to reply
Put your pencil on point C and draw a line that's perpendicular to AB. That will intersect the circle in two points, that get called E and D.
Why would the length be exactly sqrt(N)? It may be trivial but I don't get it.
Log in to reply
It's a result following directly from Pythagoras' Theorem. Note that O D = 2 N + 1 and O C = 2 N + 1 − 1 = 2 N − 1 . Thus, by Pythagoras' Theorem, we have C D = ( 2 N + 1 ) 2 − ( 2 N − 1 ) 2 = N . Thus, proven.
Relevant wiki: Area Of Triangle
The given triangles are right angled triangle, we can easily find hypotenuse using pythagoras theoram & area of the triangle.
How you created this diagram?
Observe that the length of the hypotenuse of the n t h triangle that follows the pattern is n + 1 . Since our area of the triangle required is 1, the length of one of its legs should be 2 . The hypotenuse of the n t h triangle is one leg of the n + 1 t h triangle.
So, first find which triangle has hypotenuse
2
=
4
.
n
+
1
=
2
n
=
3
So, the traingle is n + 1 = 4 i.e. D
at first if we think about triangle A.it's hypotenuse is root over 2.and area is 0.5.
in triangle B there is a hypotenuse of root over 3 and area is 0.71.
in case of triangle C it has a hypotenuse of 2 and it's area is 0.87.
in triangle D it has a hypotenuse of root over 5 and area of 1.
so.D is the answer
nice solution.
For triangle X let h X be the length of its hypotenuse. Then h C 2 = 1 2 + h B 2 and h B 2 = 1 2 + h A 2 while h A 2 = 1 2 + 1 2 = 2 .
Thus h C 2 = 1 + ( 1 + h A 2 ) = 1 + 1 + 2 = 4 . So h C = 2 . Since h C is the base of triangle D , its area is ( 1 / 2 ) ∗ 1 ∗ 2 = 1 .
The following is an expanded explanation for someone like myself, who struggles with math.
To arrive at the solution, I used two formulas:
- The formula for the area of a triangle, Area = .5(bh)
- The formula for the hypotenuse of a triangle, a 2 ∗ b 2 = c 2
In preparing to solve this problem, I wrote down the information I already knew from looking at the diagram:
- I know all of these triangles are right triangles
- I know all of these triangles have a base that is 1 unit in length
The problem asks us to determine which triangle has an area of 1. Well, since I know from the diagram that all the triangles have a base length of 1, I have enough information to determine what the height of the "winning" triangle should be:
Area = 1
Base = 1
Height = h
Using the formula for the area of a triangle, I solved for h :
1 = .5(1 * h )
1 = .5( h )
1 = .5 h
( divide both sides by .5 )
2 = h
So I now know that the triangle I'm looking for will have a base of 1 and a height of 2.
Obviously, this eliminates triangle A immediately, as triangle A has a base of 1 and a height of 1.
Now, the trickier part (for me, anyway): Using the Pythagorean theorem, a 2 ∗ b 2 = c 2 , I determined the length of the unknown height side of triangle B.
Why?
Looking at triangle A and triangle B, we see that they share a side. For triangle A, that side is its hypotenuse. For triangle B, that side is it's height. Because the value of triangle A's hypotenuse and triangle B's height are equal, if we solve a 2 ∗ b 2 = c 2 for triangle A, we will get the value of the height side for triangle B.
In this case, for triangle A:
a 2 ∗ b 2 = c 2
1 2 ∗ 1 2 = c 2
1 + 1 = c 2
2 = c 2
( take the square root of both sides )
c = 2
Now, for triangle B I know that:
base = 1
height = 2
Using the formula for area, I test to see if triangle B is my winning triangle:
Area = .5(bh)
Area = .5(1 * 2 )
Area = .707
Since the area did not equal 1, we know triangle B is not the winner.
Onward!
The next step is to repeat the use of a 2 ∗ b 2 = c 2 , this time solving for the hypotenuse of triangle B/height of triangle C. When we do this, we find:
a 2 ∗ b 2 = c 2
2 2 ∗ 1 2 = c 2
2 + 1 = c 2
3 = c 2
( take the square root of both sides )
c = 3
Now we solve for area again:
Area = .5(bh)
Area = .5(1 * 3 )
Area = .866
Just like triangle B, triangle C is not our winner!
We repeat the use of a 2 ∗ b 2 = c 2 , this time solving for the hypotenuse of triangle C/height of triangle D. When we do this, we find:
a 2 ∗ b 2 = c 2
3 2 ∗ 1 2 = c 2
3 + 1 = c 2
3 = c 2
( take the square root of both sides )
c = 4
c= 2
(oh boy!)
Now we solve for area again:
Area = .5(bh)
Area = .5(1 * 2)
Area = 1
Ding ding ding! We have a winner!
Triangle D has a base of 1 and a height of 2. Using the formula for area of a triangle when we want Area to equal 1, we find that:
1 = .5(1 * 2)
1 = 1
Triangle D is the correct answer.
The Hyponause (H) increases by the root
For A it is root 2 (ajaicent of B) Then For B it is root 3 as 1 + root 2 squared is 3 then root 3. Then for C’s H is root 4 or 2
2 times 1 over 2 is one therefore it is D
A non-mathematical intuition approach: A is clearly half a square. Find the triangle that has double the area of A. D is the most likely, as C is clearly less than double, and E is clearly more than double. The question implies that one triangle has exactly area of 1, so D must be the answer. I know this will annoy all the topologists :-)
I like to solve using a programming language as practice, in this case R:
hyp <- function(b) {
a = 1
c = sqrt(a^2 + b^2)
return(c)
}
b <- rep(0, 5)
b[1] = 1
for (i in 2:5) {
b[i] = hyp(b[i-1])
}
area = .5 * b * 1
The fourth element of the area vector equals 1, which corresponds to triangle D.
The hypotenusal series is A. root(2), B. root(3), C. root(4), D.root(5) . . . Since the a-legs of the triangles are all 1 unit, the triangle with an area of 1 will be the triangle whose b-leg = 2. This will be successor to the triangle whose hypotenuse is root(4), ie, triangle D.
Would have been a lot easier to work out with a static picture. Every time i started tracing out the lines of the triangles they would disappear when the stupid animation restarted.
The area of a right-angled triangle is 2 a b where a and b are the sides in which the angles between these 2 sides is 90 degree. So we calculate the area for every triangle (and before that we have to calculate Hypotenuse because every hypotenuse is either 'a' or 'b' of another right angled triangle. Hence we finally get the are of triangle D is 1.
I figured that since the area of a was one half it was either d or e d looked about double a in area
2 x ⋅ 1 = 1 ⇔ x = 4
we need the side length that is 4 = 2 long , and its the D triangle that has hypotenuse length 4 long
Therefore the triangle that has area of 1 unit squared is D
If you are going to observe the pattern, it will go like this.
Area of Triangle = (√n)/2
Since the area to be found is 1,
(√n)/2 = 1
√n = 2, square both sides and we have:
n = 4.
So, the triangle which has an area of 1 unit square is the sequence 4 which is D.
Therefore the answer is D
same general process but I approached it from a slightly different starting point.
I looked slowly are the desired area:
2 1 ∗ b a s e ∗ h e i g h t = 1
As we have right angled triangles, we can use the height as always 1 and the base as the line shared with the neighbouring triangle
2 1 ∗ b a s e ∗ 1 = 1
2 1 ∗ b a s e = 1
b a s e = 2
Observe the base of each triangle is is the hypotenuse of preceding one, so we need to work out the hypotenuse of each triangle until we have one that is equal to 2, then we know the answer is the triangle with that line as its base.
using Pythagoras' theorem we get the hypotenuse of each triangle to be:
t r i a n g l e A = > s q r t 2
t r i a n g l e B = > s q r t 3
t r i a n g l e C = > s q r t 4 = 2
Now we have this information we can say triangle D has a base of 2 and therefore the correct answer is D
- || ∗ ∗ d e n o m i n a t o r ∗ ∗ r o w 1 c o l 1 ∣ ∣ r o w 1 c o l 2 ∣ ∣ ∣ ∣ r o w 2 c o l 1 ∣ ∣ r o w 2 c o l 2 ||
Triangle A has a hypotenuse of sqrt 2; Triangle B has a hypotenuse of sqrt 3; Triangle C has a hypotenuse of sqrt 4 or 2. Hypotenuse of triangle C is leg of triangle D. Area of triangle D = 2 1 (2) (1) = 1
Triangle D has a hypotenuse of ✓5 which means that the longest side of Triangle D is :✓[ (✓5)^2-(1)^2]=✓(4)=2 .
Thus the area of Triangle D is :
(1/2)×1×2=1 sq. units
The letter S stands for the area of the triangle and the letter H represents the hypotenuse of the triangle. So S(A) = 1 * 1 * 1/2 = 1/2 H(A) = √(1² + 1²) = √2 According to what I have said , We can find that when it comes to the triangle C , the H of is the sqrt of (1² + (√3)²) and it equals 2 , So the S of D equals 2 times 1 then times 1/2 . The result is the number " 1 ".
Once I figured out that the hypotenuse is the height of the next triangle, along with the fact that the base is always 1, (knowing that 1/2 base times height is area) ..well 1/2 of 2 is 1 and the problem was solved when I saw the hypotenuse of 2.
The hypotenuse of triangle A is 2
The hypotenuse of triangle B is 2 + 1
The hypotenuse of triangle C is 2 + 2 = 2
We should also note that the hypotenuse of triangle C is the length of the base of triangle D. Thus the area of triangle D will be
2
2
⋅
1
=
1
The area for a triangle is 2 1 b h . The height for all the triangles is 1, and the area must be 1. Thus, we set the equation to 1, and get b = 2 . To find the base that equals 2, we know first of all, that the sum of the base and heights of all the triangles will be the root of the hypotenuse. Thus, if the hypotenuse of the 1st triangle is 2 , the hypotenuse of the 3rd triangle is 4 , which will also serve as the base for the 4th triangle, which will thus have an area of 1.
https://ibb.co/k6hvXa Solution is here
The hypotenuse of the nth triangle is ( n + 1 )
⇒ The area of the nth triangle is 2 1 ∗ n = 2 n
Area = 1
⇒ 2 n = 1
⇒ n = 2
⇒ n = 4
⇒ Triangle D has area 2
Triangle A has hypotenuse 2 and area 2 1 .
Triangle B has hypotenuse 3 and area 2 2 .
Triangle C has hypotenuse 4 = 2 and area 2 3 .
Triangle D has hypotenuse 5 and area 1.
Triangle E has hypotenuse 6 and area 2 5 .
Therefore, we can see that Triangle D has an area of 1.