30 of 100: Four Circles
A right triangle contains four congruent circles that touch the sides as shown. What is the radius of each circle?
You can assume all points that appear to touch are touching.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
30 solutions
This is a wonderfully elegant solution, involving nothing more complicated than the area of a triangle and Pythagoras' theorem. I like it a lot.
Such a clever solution! I solved it using angle bisector theorem. In my oppinion, this was one of the most interesting problems so far, not just because it's intriguing geometric puzzle, but because there is such a variety of solutions, I enjoyed reading them all! Great community!
Excellent solution. It's very nice.
Great solution! Definitely the simplest possible solution.
Excellent.
Never thought of this way. Thanks.
What an elegant solution!
i love pythagoras !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Great solution, I would've never thought about it
How clean! How clear! How simple! My!
I solved it this way! It is good :)
Could you please explain it a little more? This way looks awesome, thanks.
This is called a neat proof
why 6r + 4r = 8?
I REALLY like this but I think you could make it simpler with just one variable
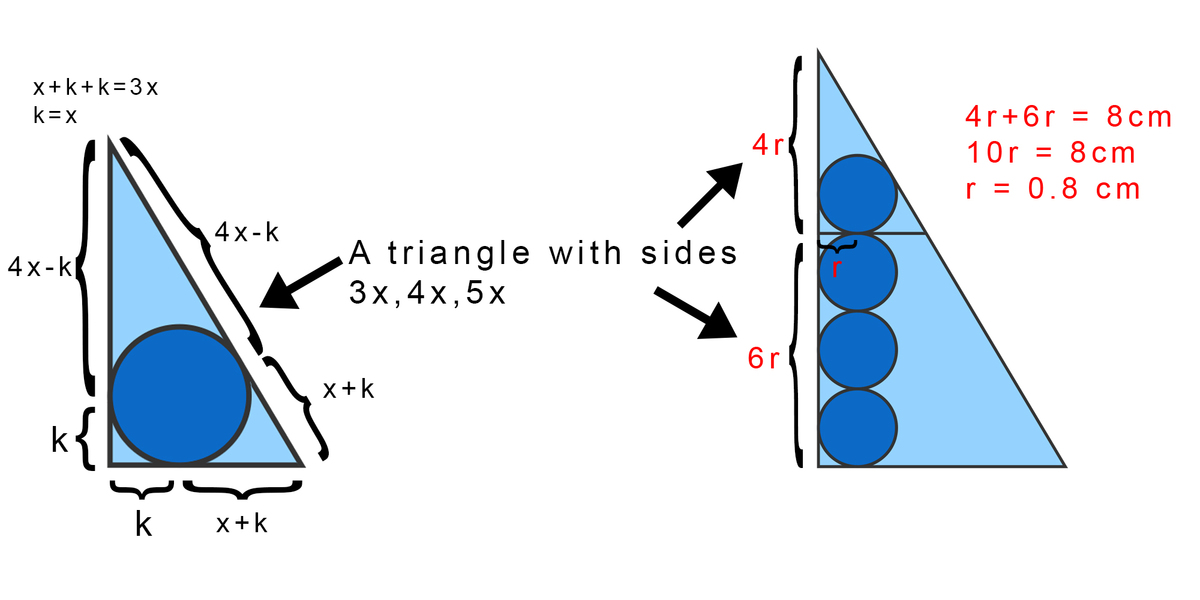
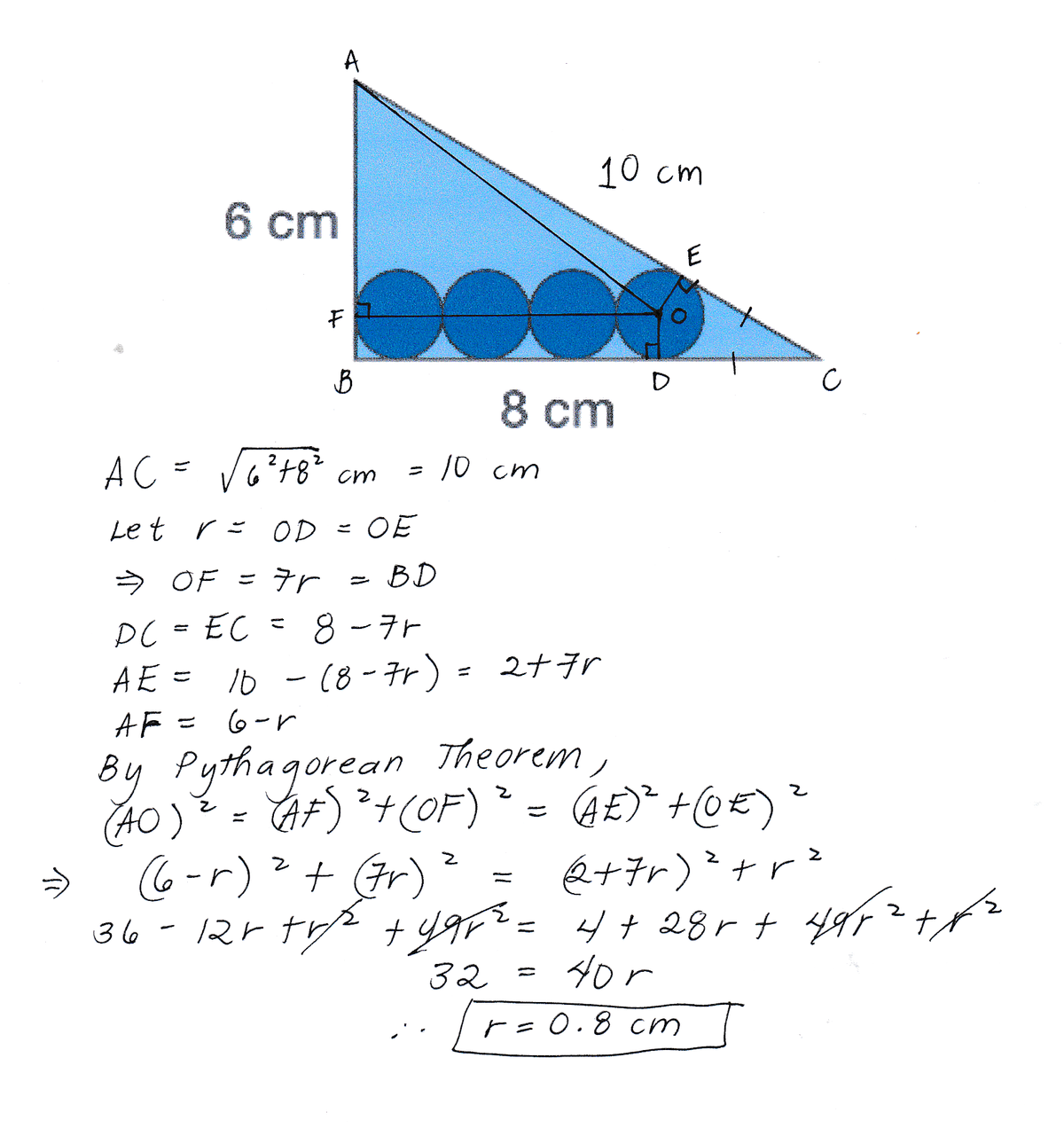
Denote the points as the above figure. Let r is the radius of each circle.
Applying the Pythagore theorem, B C = A B 2 + A C 2 = 1 0 cm.
Applying the angle bisector theorem, we have D B A D = B C A C = 5 4 .
Hence, A B A D = A D + D B A D = 9 4 or A D = 9 4 ⋅ 6 = 3 8 cm.
Look at the figure, we get I H = r , A H = 7 r , and H C = 8 − 7 r .
Applying the Thales theorem, we have H C I H = A C A D = 3 1 or 8 − 7 r r = 3 1 .
This implies that r = 5 4 = 0 . 8 cm.
Pythagore theorem. The goriest theorem yet.
How is your penultimate line Thales' Theorem as opposed to just similar triangles?
Log in to reply
In the French educational system this is called the Thales' Theorem, while the one about a triangle inscribed in a circle you might be referring to does not have a particular name.
Log in to reply
I'm not referring to any circles, just two similar triangles!
I used sin(phi), where phi is the angle ACB, and knowing that in the small triangle angle ACD will be ACB/2, I calculated r. I consider the above solution a better one, cause I had to use a calculator to find the answer.
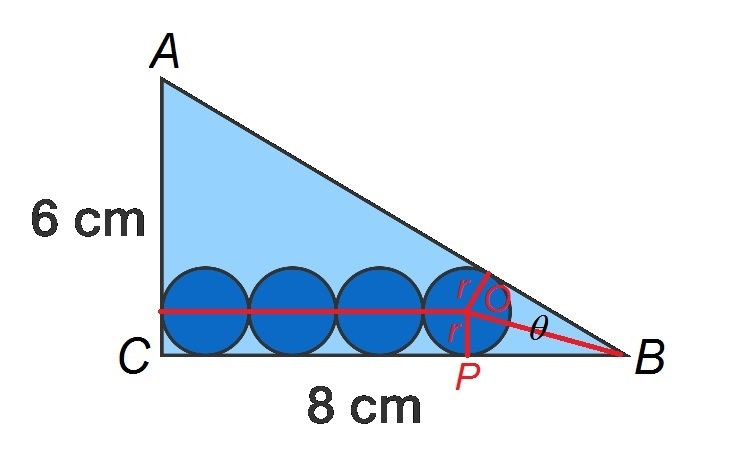 Let the triangle be
A
B
C
, the radius of the circles be
r
, the center of the right circle be
O
, the perpendicular from
O
meet
B
C
at
P
and
∠
A
B
C
=
θ
.
Let the triangle be
A
B
C
, the radius of the circles be
r
, the center of the right circle be
O
, the perpendicular from
O
meet
B
C
at
P
and
∠
A
B
C
=
θ
.
Then we note that tan 2 θ = B P O P = 8 − 7 r r . Therefore,
8 − 7 r r ⟹ 8 − 7 r r 3 r 1 0 r ⟹ r = tan 2 θ = sin θ 1 − cos θ = 5 3 1 − 5 4 = 3 1 = 8 − 7 r = 8 = 0.8 cm As suggested by Atomky Jahid: tan 2 x = sin x 1 − cos x
Thanks to @Atomsky Jahid .
I had this one in mind as well (+1) Perhaps it would be even shorter if the identity tan x/2 = (1-cosx)/(sin x ) was used.
Log in to reply
You are good with tan 2 x = ( 1 − cos x ) sin x . I didn't know that.
Log in to reply
It's tan 2 x = sin x 1 − cos x .
Log in to reply
@Atomsky Jahid – No wonder, I didn't get it.
Log in to reply
@Chew-Seong Cheong – I have used your suggestion. Thanks.
@Atomsky Jahid – Isn't that precisely what I said ?
Log in to reply
@Aditya Dhawan – Yes. Maybe he didn't notice the slash between (1-cosx)/(sinx).
Log in to reply
@Atomsky Jahid – Perhaps. I don't have access to my computer right so can't use Latex right now. Never mind
Log in to reply
@Aditya Dhawan – Your comment has got a fair amount of upvotes. So, chill! PS: You can also use Latex in mobile.
Exactly my approach.
What is y?
I think the solution is good, but the drawing is confusing. The horizontal arrow marking x is incorrect, it should be marking the distance between the right angle vertex of the orange triangle and the rightmost vertex of the original triangle. Similarly, y is not clear. The blue arrow marking y supposed to mean the distance between the top vertex of the orange triangle and the base of the original triangle, but because it is not placed at the correct location, it is hard to see. Essentially, there is a triangle that should have been marked: it is the triangle you get when you chop off the rightmost tip of original triangle by a vertical line that goes through the orange triangle's vertical side. This triangle is similar to the original triangle, and x and y are the sides of that triangle.
Nice one +1
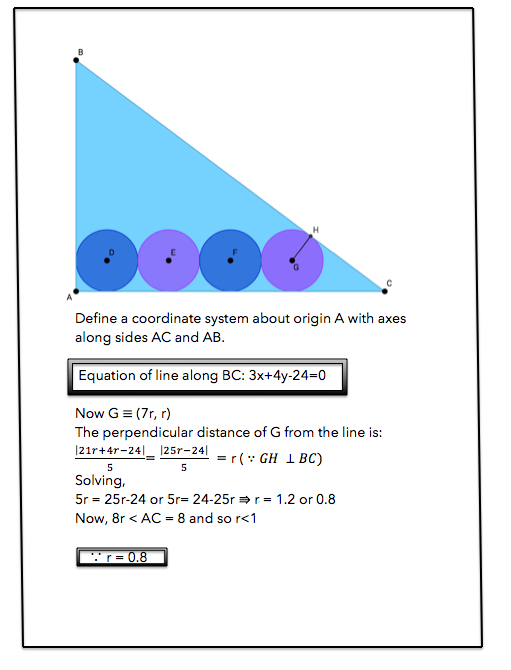
Why is the denominator 5 in the formula for distance of G from the line? I don't get it.
Log in to reply
The distance of a point P ( h , k ) from the line L ≡ a x + b y + c = 0 is given by a 2 + b 2 ∣ a h + b k + c ∣ . Putting a = 3 and b =4 results in the cited expression.
What did you use to make this? Mathematica?
And to make the text outlining the steps? LaTeX? Just curious, I like this answer a lot.
Elegant! Thank you.
This is a different approach that I haven't seen anyone do before. WARNING: More math is involved in this one than the others.
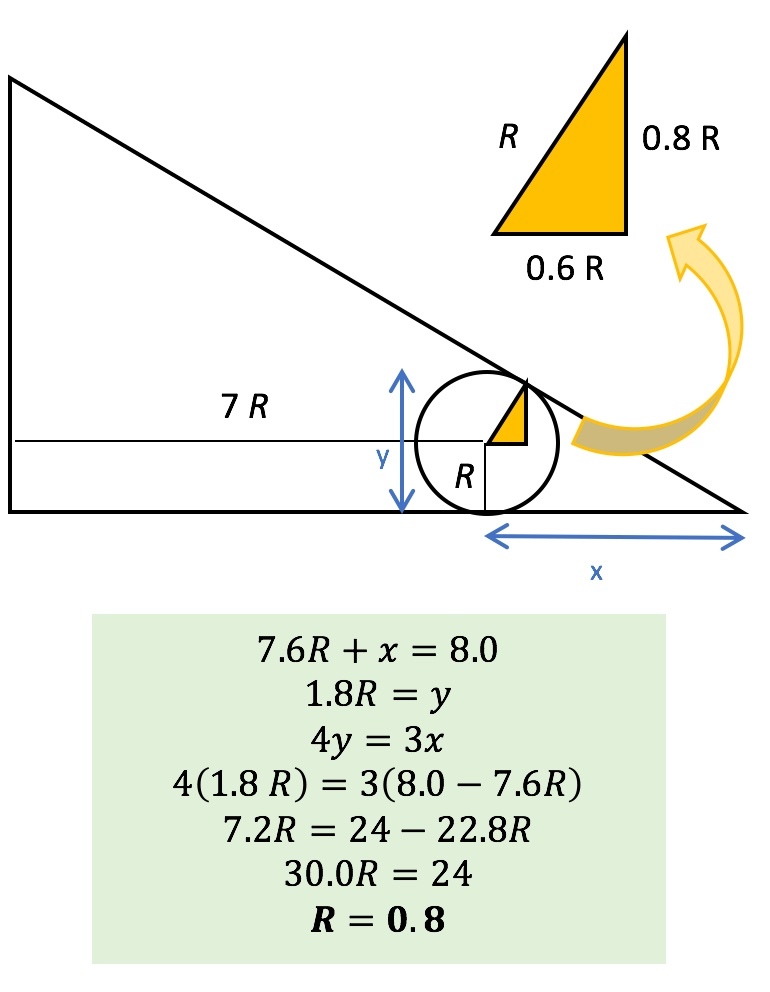
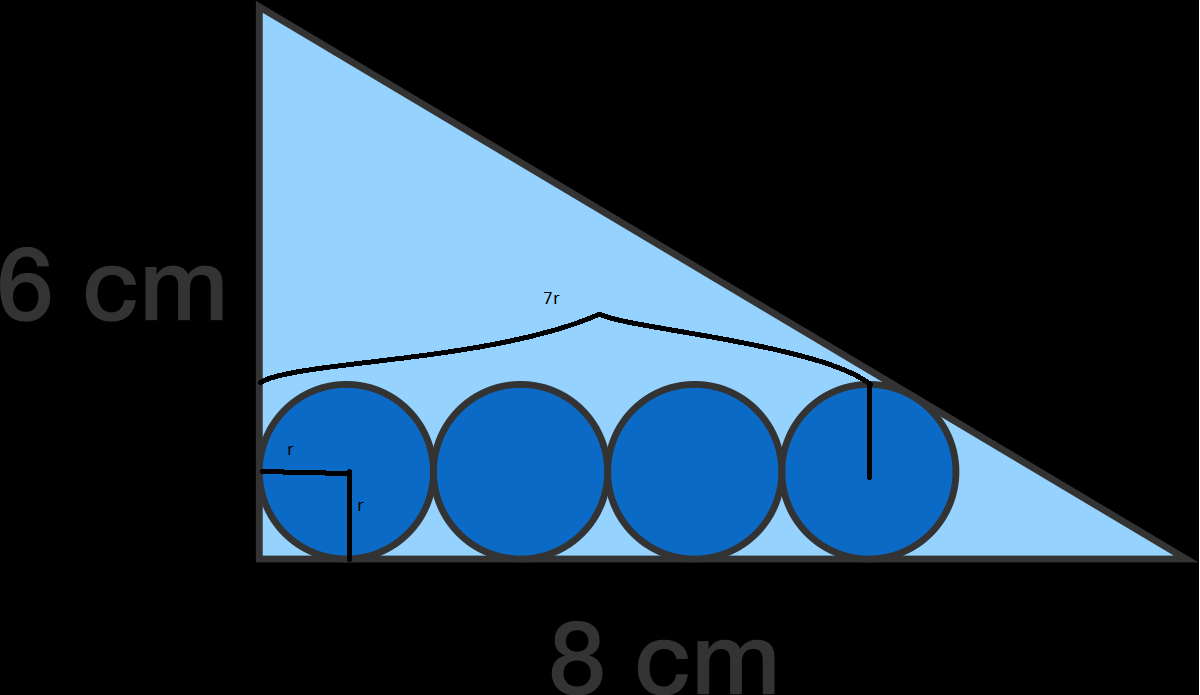 From the diagram, you can see that the center of the fourth circle, which I will call C, is at (7r, r), if we assume that (0,0) is at the right angle, and the triangle is in the positive direction.
The point of intersection, which I will call P, is at (x,y), and the line CP has length r and is perpendicular to the hypotenuse of the triangle, which goes from (0,6) to (8,0), so has slope
m
=
−
3
/
4
.
From the diagram, you can see that the center of the fourth circle, which I will call C, is at (7r, r), if we assume that (0,0) is at the right angle, and the triangle is in the positive direction.
The point of intersection, which I will call P, is at (x,y), and the line CP has length r and is perpendicular to the hypotenuse of the triangle, which goes from (0,6) to (8,0), so has slope
m
=
−
3
/
4
.
From this, it can be concluded that y = 6 − 3 x / 4 . Furthermore, because line CP is perpendicular to the hypotenuse, it must have slope m=4/3. Because of the 3-4-5 pythagorean triple, this means that CP goes to the right 3 r / 5 units and goes up \(4r/5) units.
If you plug in values, then you get that P is at \((7r + 3r/5, 9r/5)\). If you plug those values in for x and y into the equation at the start of the previous paragraph, then you get that 9 r / 5 = 6 − 3 ( 7 r + 3 r / 5 ) / 4 , which can be algebraically manipulated to r = 4 / 5 , which is the answer.
This is the approach I took.
This was my method also. I think it's much more intuitive than the geometric and trigonometric solutions others posted.
Just to clarify, (at the risk of restating the obvious),atan stands for arctan or tan^-1 (the inverse of the tan function, not the reciprocal)
Log in to reply
I made a mistake in my initial solution where i had inadvertently stated tan(ABC) = atan(6/8) instead of angle ABC. Apologies for the typo.
Similar approach.
Also, i have not formally proved that the two trns formed by the ray to the center of the circle are congruent and hence the ray bisects angle ABC. But we have two right trns with a common hypotenuse and two corresponding sides that are congruent (the radii). So , it seemed too obvious to need a formal proof
My challenge is a test that I have failed by running out of time. So I'm going for speed.
I'm in training to teach math, so I'm attempting meta-cognition on my process, and this is how it went. This is going to be ugly. Real mathematicians should avert their eyes. I have a different process results in a much prettier explanation that I can clean up and present as a proof. I like that process. But that process takes time. That process cost me a standardized test last month.
I looked at the diagram. If the radius is 1, then the circles cover the whole base and angle at the right is a right angle. We are presumably using Euclidean geometry here, so we know it is less than that.
But visually, not a whole lot less than that. The empty triangle past the last circle is small.
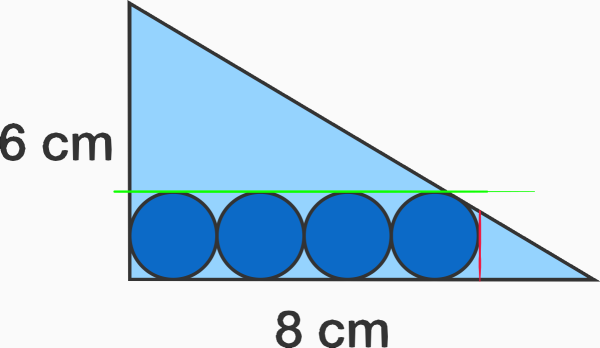
This is multiple choice, so I probably don't need a precise answer. The base of that little triangle on the right, with the red side, is 8 − 8 r cm because the red line is at the end of 4 circles. The height of that red side is 3/4 of that, because the triangle is similar to the big 6-8-10 triangle which has a 3/4 ratio.
My first guess is 0.8 cm because I think the answer is close to (but less than) 1 cm. 0.5 cm would mean the circles end 1/2 way across the base, and that would be a very acute triangle.
At the first guess, 0.8 cm, the red side is 1.2 cm long. And the green line tangent to the tops of the circles is 1.6 cm high. So that's plausible. But is it right? I don't want to mess with the picky non-right triangle work if I don't have to.
Next guess, 0.7 cm. Now the red side is 1.8 cm. And the green line is at 1.4 cm. So the hypotenuse misses the top of the circle before it even gets to the front of the circle. The 0.7 cm radius is too small.
0.8 cm it is.And the answer comes back "correct." Yay.
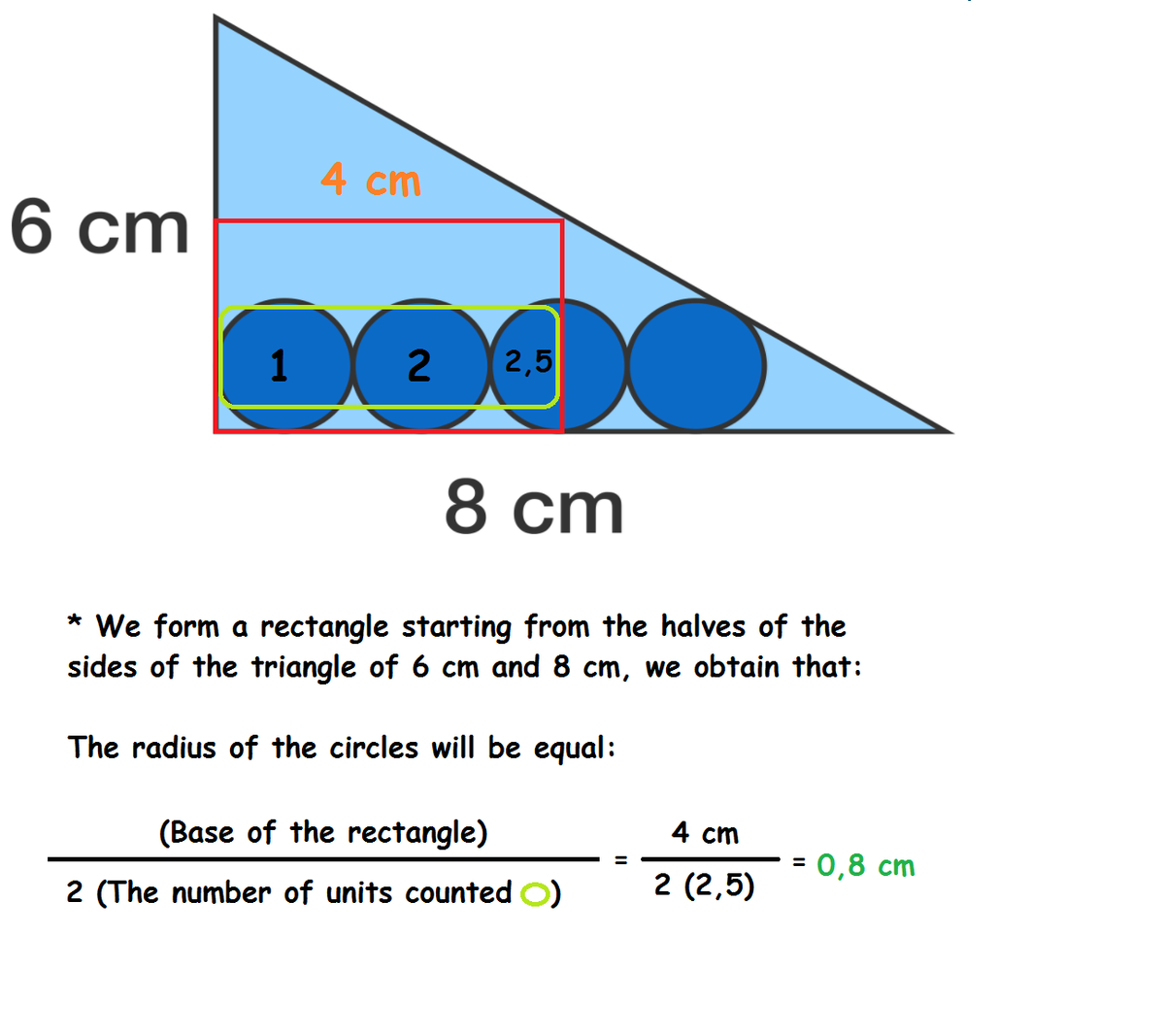
I just eyeballed it. The centerpoint of the circle above the "cm" of "8 cm", is halfway between the 8 cm. Making 5 radiuses 4 cm.
4/5= 0.8
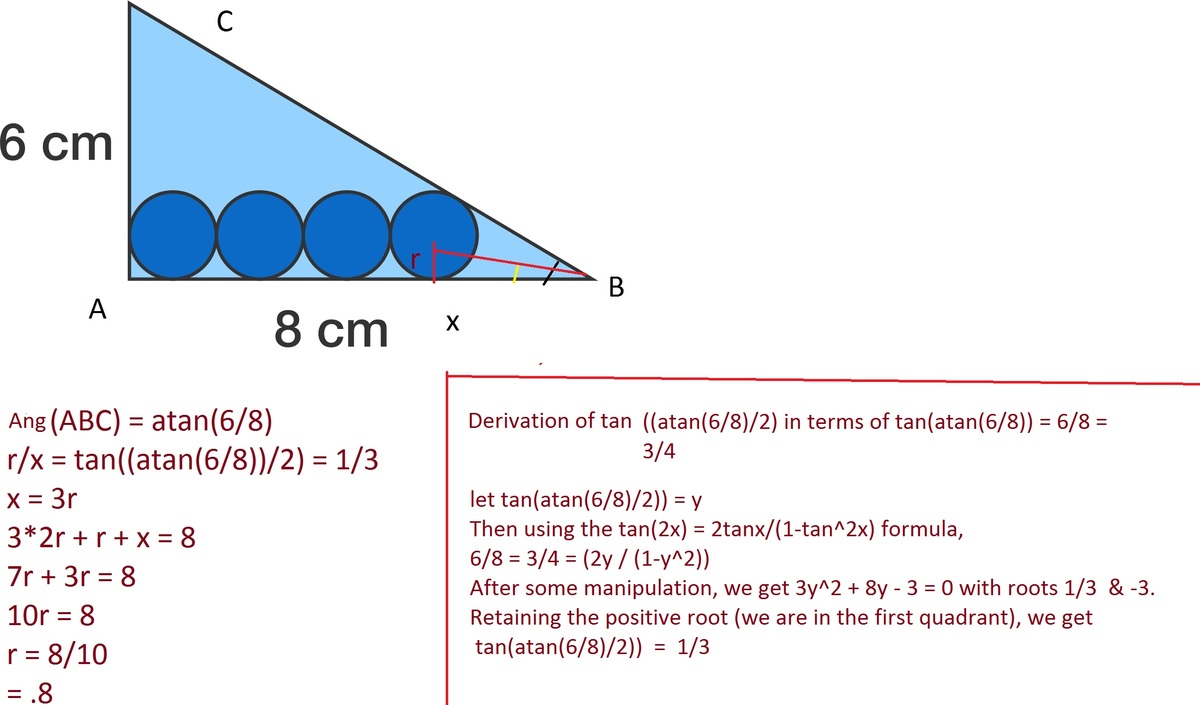
tan(A)=6/8=3/4 Therefore, tan(A/2)=1/3=r/(8-7r) or r=0.8
Based on the picture, if it takes 4 circles to be equivalent to 8cm, then it means that 5 circles are equivalent to 8cm. So, if you can do the following to solve to find each circle's radius (in cms):
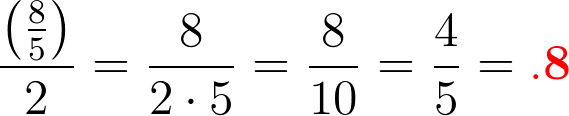
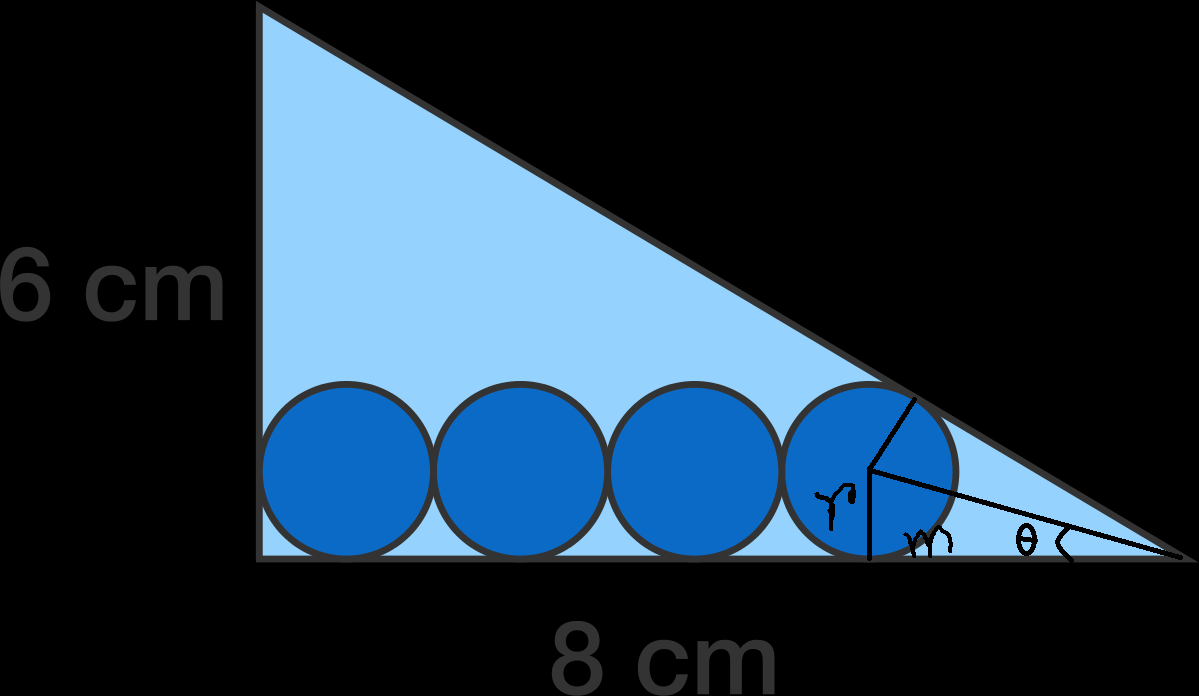 Here,
tan
2
θ
=
4
3
and
tan
2
θ
=
1
−
tan
2
θ
2
tan
θ
solving, we get
tan
θ
=
3
1
,
−
3
now, taking the positive value,
8
−
7
r
r
=
3
1
solving,
r
=
5
4
Here,
tan
2
θ
=
4
3
and
tan
2
θ
=
1
−
tan
2
θ
2
tan
θ
solving, we get
tan
θ
=
3
1
,
−
3
now, taking the positive value,
8
−
7
r
r
=
3
1
solving,
r
=
5
4
Though, excellent solutions have been submitted by others, there is yet another simple solution.
At the end of 4th circle, draw a tangent perpendicular to the 8cm base, intersecting base at A, hypotenuse at B and is tangent at P. The triangle formed by line AB with vertex at smallest angle is similar to large triangle with sides 6, 8 and hypotenuse 10. The base length of small triangle is (8 - 8r), r being radius of circles.
The other two sides being proportionate in lengths, would be (6 - 6r) and (10 - 10r).
The lengths of two tangents to 4th circle from vertex at smallest angle are (8 - 7r).
Now, the lengths of two tangents to the 4th circle from point B are,
1. Along the hypotenuse,
Tangent length from vertex - the hypotenuse length of small triangle,
(8-7r) - (10-10r) = 3r - 2,
2. Tangent BP = (6 - 6r) - r = 6 - 7r,
These two tangents being equal, we have
3r - 2 = 6 - 7r.
Or, 10r = 8 or r = 0.8.
Where the right hand most circle touches the hypotenuse of the triangle, it creates a point which is 7r (let r represent the length of a circle radius) along and 2r up from the 90 degree corner of the triangle. This creates two smaller congruent triangles, one of which has a height of 2r and the other with a base of 7r. The length of the base of the 2r triangle would be (2r * (8/6) ) = 2 2/3. The base 8 is therefore equivalent to 7r + 2 2/3r = 9 2/3 r; r = 8/9.667, which is roughly 0.8
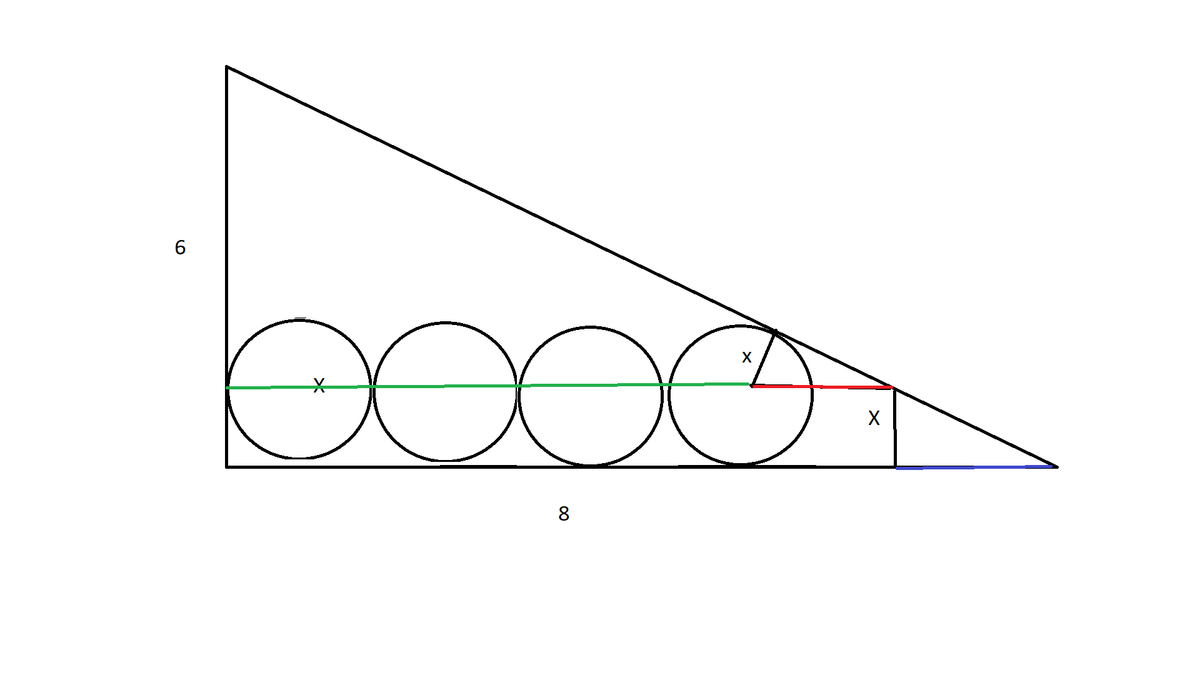
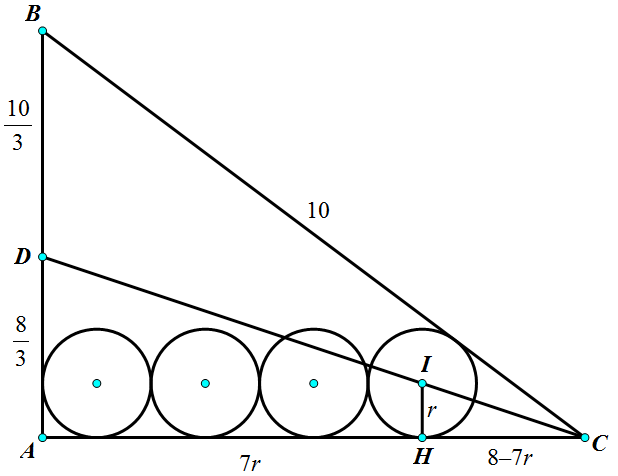
The radiius of the circle is x . The length of the green line is 7 x The length of the red line is 3 5 x (3-4-5 Triangle)
The Length of the blue line - bottom of the last little triangle on the right - is 3 4 x
We know the bottom line is 8 so 8 = 7 x + 4 x / 3 + 5 x / 3
8 = 7 x + 9 x / 3
8 = 1 0 x
x = . 8
Note that it is easy to bound the solution of this problem. Given that there are exactly 4 circles that fit within this space, it is not possible to fit another circle in the remaining space. That means that the vertical size of the small triangle should be smaller than 2 ∗ r , for a circle of radius r . Therefore we have:
( 8 − 8 ∗ r ) ∗ 6 / 8 < 2 ∗ r
= > 6 ∗ ( 1 − r ) < 2 ∗ r
= > 6 < 8 ∗ r
= > 0 . 7 5 < r
Therefore the only answer that fulfills the requirement is 0.8
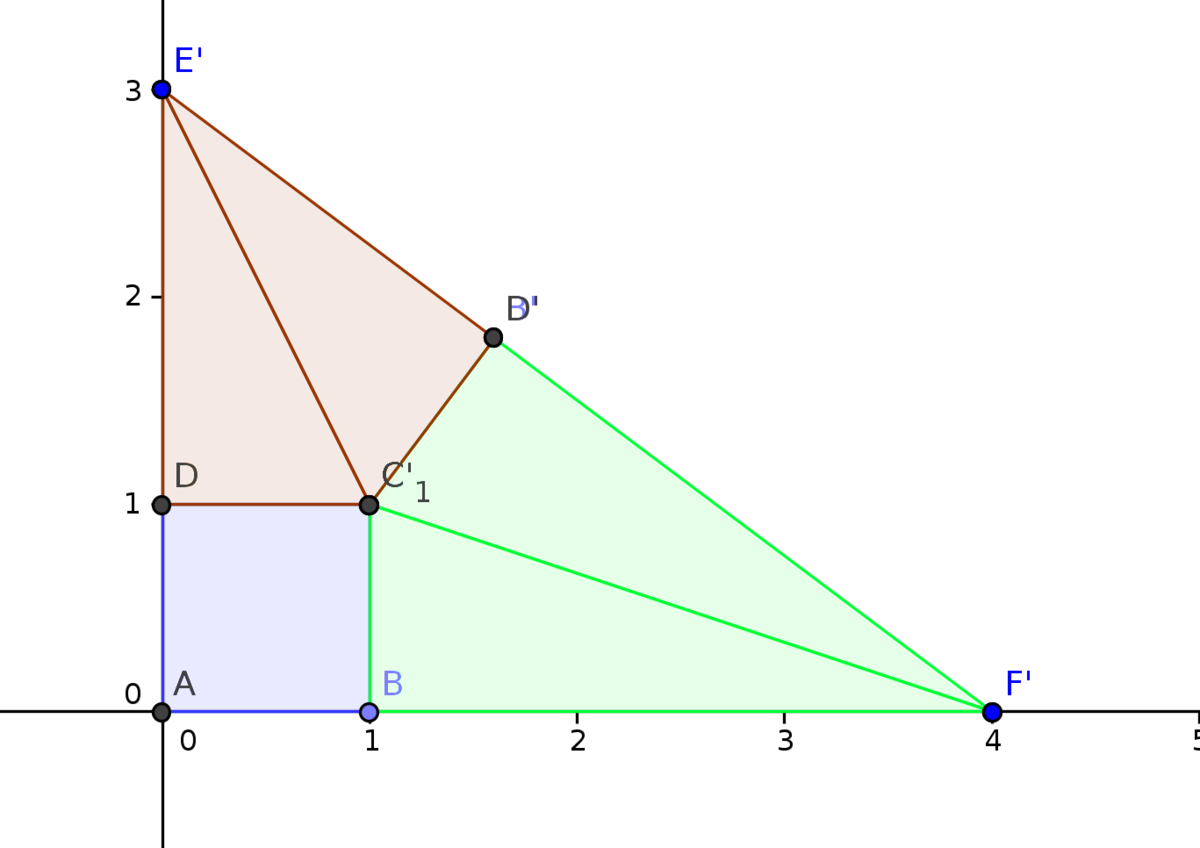
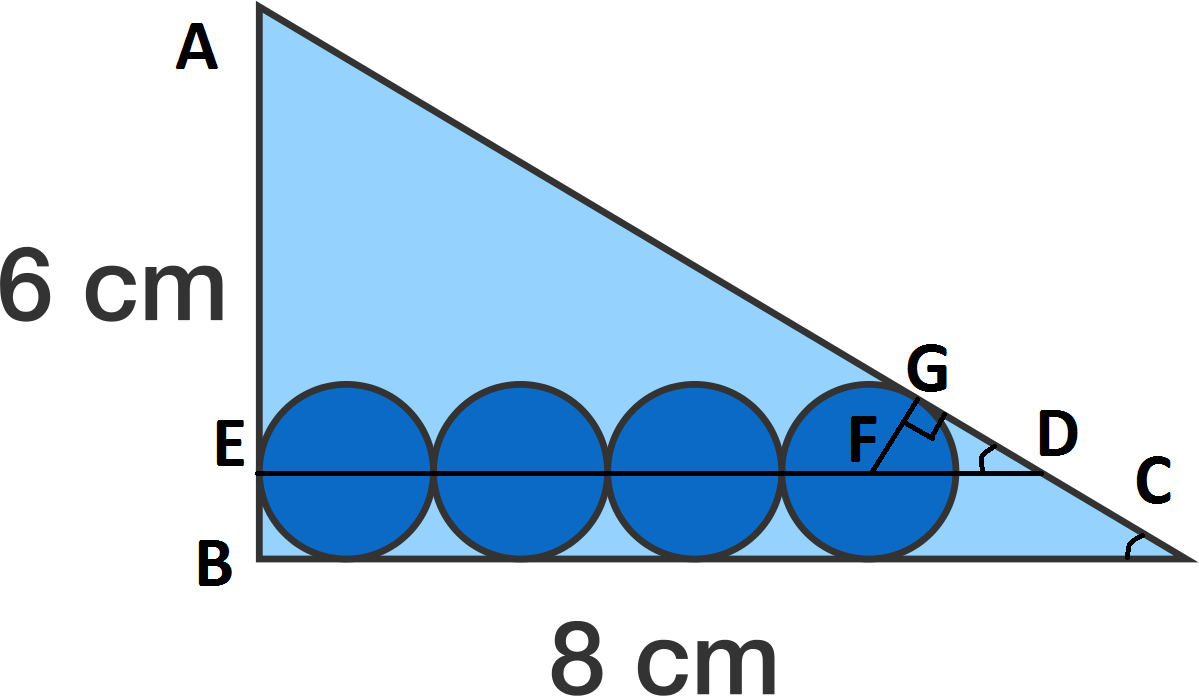 First of all, we can note that
A
C
=
1
0
using the pythagorean theorem:
A
B
2
+
B
C
2
=
A
C
2
6
2
+
8
2
=
A
C
2
3
6
+
6
4
=
1
0
0
=
A
C
2
⟹
A
C
=
1
0
0
=
1
0
Now, we can draw a horizontal line through all of the centers of the circles (
E
D
). Notice, the radius
F
G
is tangent to
A
C
, therefore, they form a right triangle. Now, notice angle
B
C
A
is equal to angle
F
D
G
. Therefore,
Δ
A
B
C
Δ
F
G
D
. Now, we can form another similar triangle dilated about point
A
such that
B
′
C
′
lie above the circles. Now, we have an easy ratio to work with. We notice
B
C
A
B
=
E
D
A
E
. We can substitute in values and get
4
3
=
r
(
7
+
cos
(
∠
D
F
G
)
)
6
−
r
(
1
+
sin
(
∠
D
F
G
)
)
Using the similar triangle properties from earlier. we know
sin
(
∠
D
F
G
)
=
1
0
8
=
5
4
and
cos
(
∠
D
F
G
)
=
1
0
6
=
5
3
. Now, we can solve for r.
r
(
7
+
5
3
)
6
−
r
(
1
+
5
4
)
=
4
3
2
4
−
5
3
6
r
=
5
1
1
4
r
2
4
=
5
1
5
0
r
=
3
0
r
⟹
r
=
5
4
First of all, we can note that
A
C
=
1
0
using the pythagorean theorem:
A
B
2
+
B
C
2
=
A
C
2
6
2
+
8
2
=
A
C
2
3
6
+
6
4
=
1
0
0
=
A
C
2
⟹
A
C
=
1
0
0
=
1
0
Now, we can draw a horizontal line through all of the centers of the circles (
E
D
). Notice, the radius
F
G
is tangent to
A
C
, therefore, they form a right triangle. Now, notice angle
B
C
A
is equal to angle
F
D
G
. Therefore,
Δ
A
B
C
Δ
F
G
D
. Now, we can form another similar triangle dilated about point
A
such that
B
′
C
′
lie above the circles. Now, we have an easy ratio to work with. We notice
B
C
A
B
=
E
D
A
E
. We can substitute in values and get
4
3
=
r
(
7
+
cos
(
∠
D
F
G
)
)
6
−
r
(
1
+
sin
(
∠
D
F
G
)
)
Using the similar triangle properties from earlier. we know
sin
(
∠
D
F
G
)
=
1
0
8
=
5
4
and
cos
(
∠
D
F
G
)
=
1
0
6
=
5
3
. Now, we can solve for r.
r
(
7
+
5
3
)
6
−
r
(
1
+
5
4
)
=
4
3
2
4
−
5
3
6
r
=
5
1
1
4
r
2
4
=
5
1
5
0
r
=
3
0
r
⟹
r
=
5
4
The following illustration builds an argument that relies on the following three key points: [1] the incircle of a scaled (3n, 4n, 5n) right triangle has a radius r = n. For example, a (3, 4, 5) right triangle has an incircle with radius r = 1. The result that r = n for a (3n, 4n, 5n) right triangle is achieved by angle bisector properties and congruent triangles and the fact that the perimeter of the right triangle is 3n + 4n + 5n = 12n. [2] the (3n, 4n, 5n) right triangle with the incircle is similar to the (6, 8, 10) right triangle. [3] the right triangle with the incircle is located in the context of the problem, which enables the bottom side of the (6, 8, 10) right triangle (i.e. the side of length 8) to be measured in terms of the radius of the incircle.
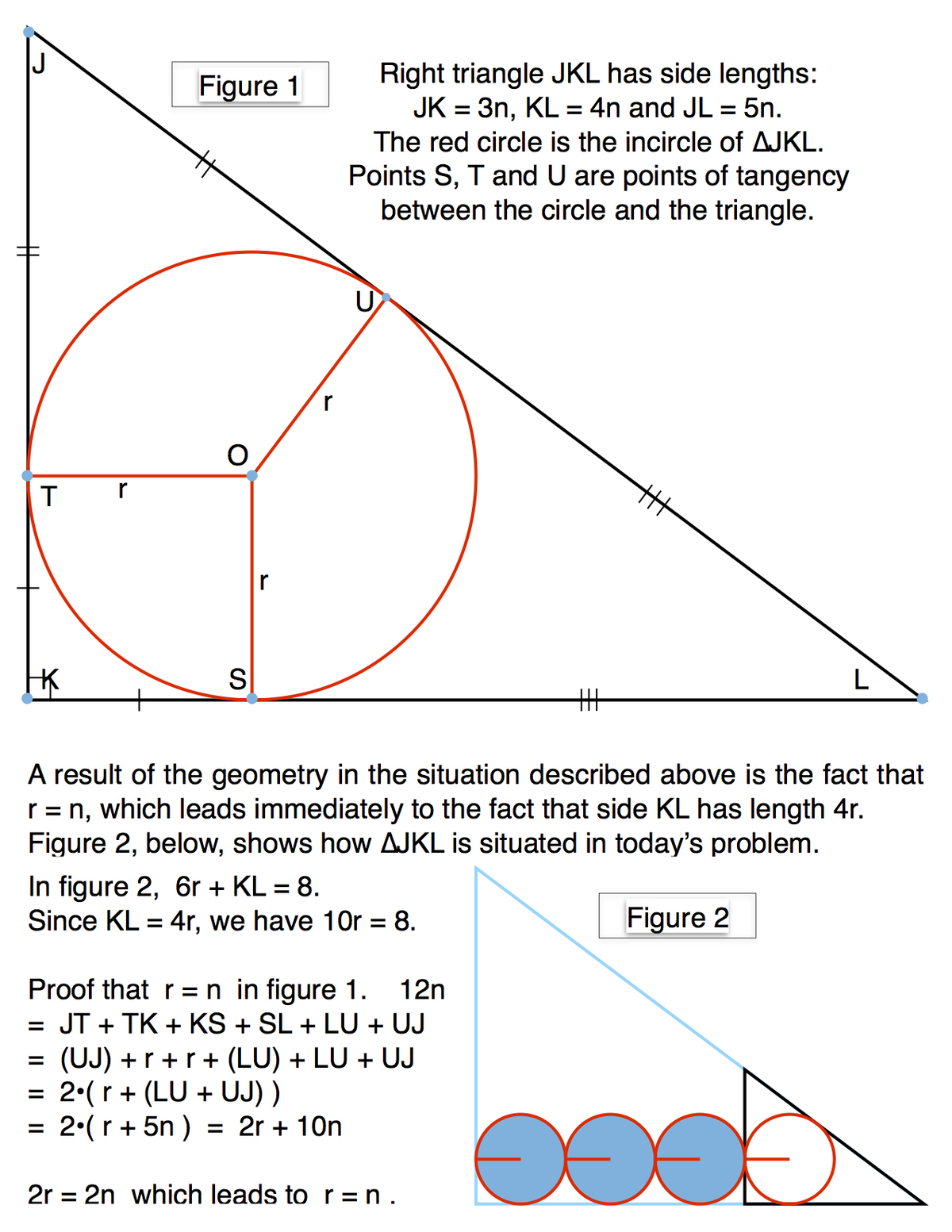
Since 10r = 8, r = 8/10 = 0.8 .
BTW, when the overall figure is drawn to scale, the distractors 0.5 and 0.6 can easily be eliminated. I would suggest a more challenging set of distractors: 0.7, 0.75, 0.8 and 0.85 .
Okay, so I think we can take advantage of the fact that this is a multiple choice problem to solve it without explicitly solving for the radius of the circle:
Suppose you drew a line perpendicular to the base of the triangle and tangent to the rightmost circle, labeling the intersection point with the hypotenuse A and the intersection with the base B and the lower right vertex of the triangle C , like so:
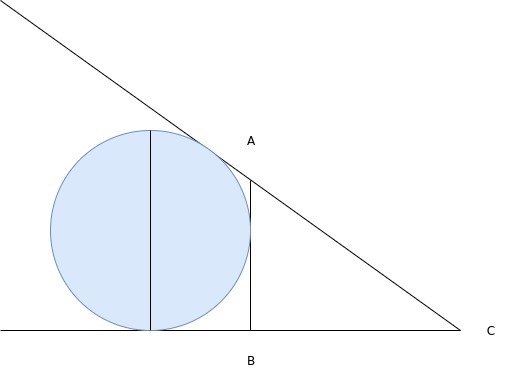
Length A B has to be less than the height of the circle, because if you assume the contrary the hypotenuse would have to intersect the base of the triangle on the other side of the circle (or be parallel to the base if you suppose them to be equal). Therefore, if r is the radius of the circle, A B < 2 r .
Also, length A C will just be whatever remains after taking 4 circle-widths ( which is 2 r ) away from the base of the original triangle:
A C = 8 c m − 4 ∗ 2 r = 8 − 8 r = 8 ( 1 − r )
But since triangle ABC is similar to the large triangle,
A B = 6 / 8 ∗ A C = 6 ( 1 − r )
Therefore, since A B < 2 r :
6 ∗ ( 1 − r ) < 2 r 3 − 3 r < r 3 < 4 r 3 / 4 = . 7 5 < r
The only possible solution for r that falls above this lower bound is .8 cm.
Now, to be fair, this wouldn't have worked if e.g. .9 cm was one of the choices, but in this case we got lucky and a lower bound was enough. Note that we also could have quickly gotten an upper bound by noticing that eight radius is less than the base, so 8 > 8 r → 1 > r .
Applying Thales theorem: 3/r = 8/8-7r ; r= 0.8 cm
7r+x=8.....(1) 2r/6=×/8.....(2) From eqn.2 ×=16r/6. So 7r+×=7r+16r/6=8 And 58r/6=8 Finally r=8.27
If you recognize that this problems involves a 3-4-5 triangle and that all such triangles are made up of 1:2 and 1:3 triangles you can follow the idea of many of the other solutions but skip a lot of steps and go directly to
8 − 7 r r = 3 1
If x-axis is along the side 8 and y-axis is along the side 6. Let the radius of the circle be r. The equation of the line along the hypothenuse is:
x/8 + y/6 = 1, or 6x + 8y - 48 = 0.
The center of the circle touching the hypothenuse has coordinate (7r, r). The distance from this point to hypothenuse is:
r = |42r + 8r - 48|/10,
then, if:
10r = 50r - 48, 40r = 48, r = 1.2
Since 8r < 8, then r < 1. So this solution is acceptable. Therefor:
10r = 48 - 50r, 60r = 48, r = 0.8.
Therefore the radius of each circle is 0.8 cm.
Set up coordinates A(8,0), B(0,6), and the origin as the vertices of the triangle, and let r be the circles' radius. Note that the center of the rightmost circle is P(7r,r), and that the perpendicular distance from P to line AB is r. On the other hand, that distance is also |50r - 48|/10, applying the formula found in https://brilliant.org/wiki/distance-between-point-and-line/. This yields roots r = 0.8 and r =1.2. The smaller root corresponds to the diagram as shown, while the larger root puts the rightmost circle outside (but still tangent to) the triangle. QED
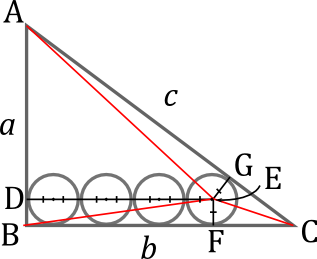 let
a
=
∣
A
B
∣
let
a
=
∣
A
B
∣
let b = ∣ B C ∣
let c = ∣ C A ∣ = a 2 + b 2
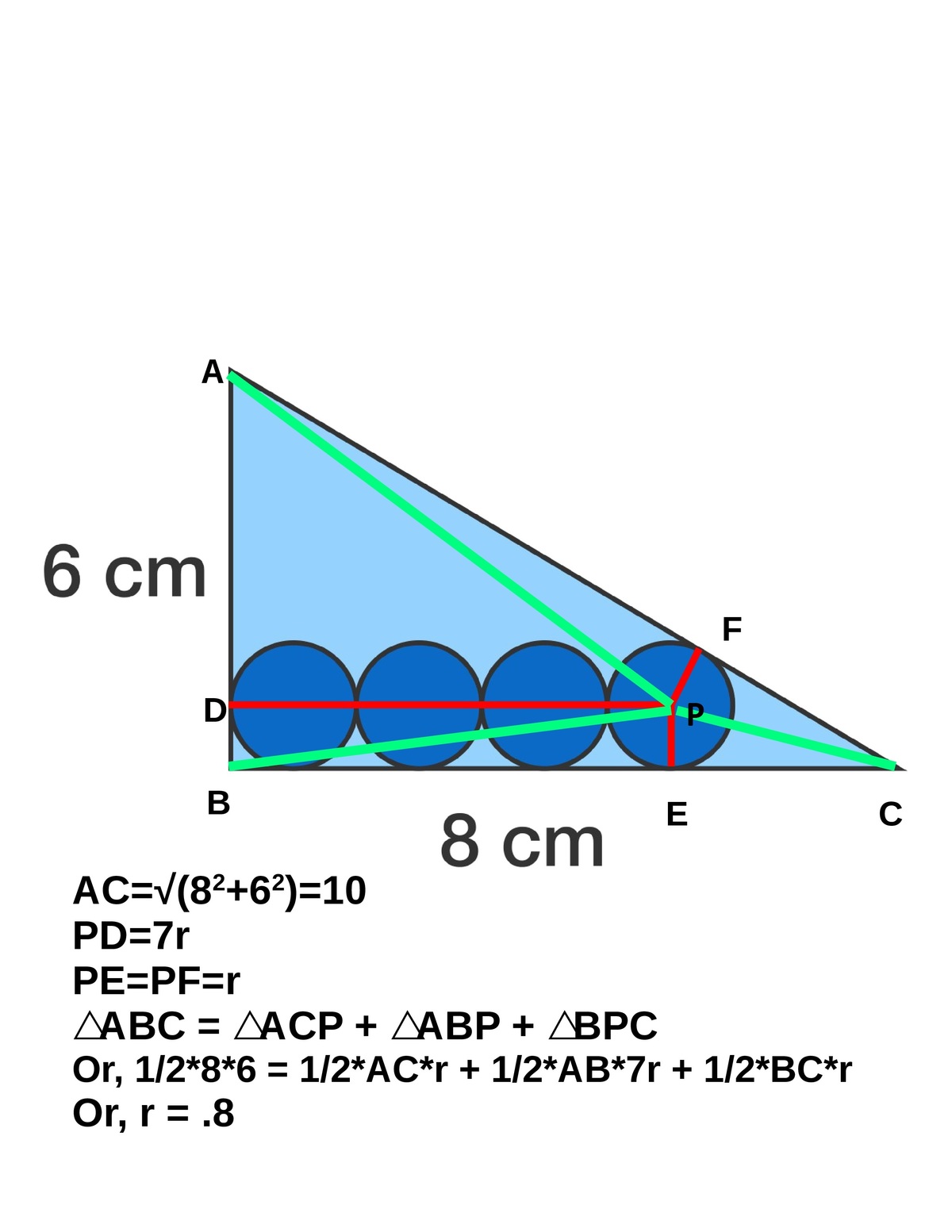
∣ E F ∣ ≡ ∣ E G ∣ = r
⇒ ∣ D E ∣ = 7 r
The area of the largest triangle is the sum of the constituent triangles: ∣ Δ A B C ∣ = ( ∣ Δ C A E ∣ + ∣ Δ A B E ∣ + ∣ Δ B C E ∣ )
2 1 ∣ A B ∥ B C ∣ = 2 1 ( ∣ C A ∥ E G ∣ + ∣ A B ∥ D E ∣ + ∣ B C ∥ E F ∣ )
⇒ a b = c r + a 7 r + b r = r ( 7 a + b + c )
⇒ r = 7 a + b + c a b = 7 a + b + a 2 + b 2 a b
Substitute a = 6 ; b = 8
r = 6 0 4 8 = 0 . 8
You can fit another cycle at the end to just utilize the length so you would only have to do .8 x 2 getting you 1.6 then multiply that by 5 which ends up getting you 8.