33 of 100: The First Rule of Octagon Club Is Don't Talk About Octagon Club
What fraction of the regular octagon is shaded red?
If you're ever having trouble in a geometry problem, try adding some line segments!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Beautifully simple !!
I was about to post the same solution. I think this is the simplest way.
That's how I did it!
Simplest!!
This question appeared in the Australian Mathematics Competition 2008
Very cool!
Nice solution!!
It took me 20 minutes to think about this although i used the circumscribed circle (also with center O) way. you just create point C' in one of the nearest vertesies (the left or the right), and you have some theorem about circles arches witch states the same thing also triangle ABC' has the same area as triangle ABC.
Easy and simple. You are smart.
i don't see that transformation from 1 to 2 easily... unless with calculus
Log in to reply
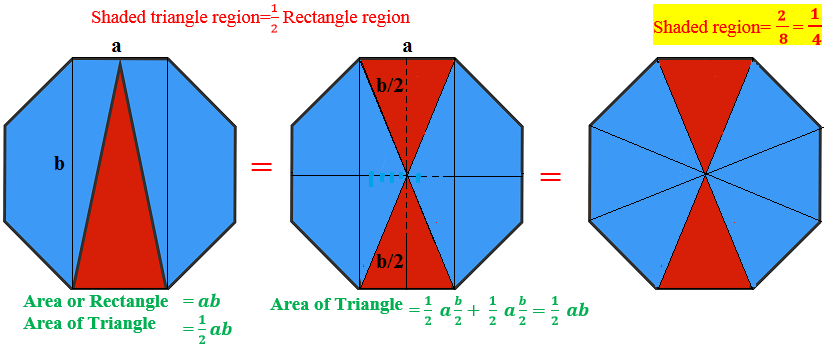
I added the required information for your understanding. Just need formula of rectangle and triangle.
Log in to reply
well, that's with calculus xD
Log in to reply
@Samuel Silva – i think it's actually just algebra, this solution doesn't require calculus
Beautiful solution.
Much better solution than mine. Thanks.
Just an another way to see it!
 There are
8
equal triangles (eight isosceles right triangles with equal hypotenuse, which is indeed the side of octagon) and
4
equal rectangles (with a length equal to side of octagon and a width equal to leg of isosceles right triangle) in the picture. Thus area
1
is equal to area
2
. Shaded region (red color in the original figure) is half of the area
1
, and, thus, its
4
1
of the total area.
There are
8
equal triangles (eight isosceles right triangles with equal hypotenuse, which is indeed the side of octagon) and
4
equal rectangles (with a length equal to side of octagon and a width equal to leg of isosceles right triangle) in the picture. Thus area
1
is equal to area
2
. Shaded region (red color in the original figure) is half of the area
1
, and, thus, its
4
1
of the total area.
This is an interesting way to see this. Could you please clarify how can you prove that triangle in the center has the same area that triangle in the bottom left, for example? Thank you.
Log in to reply
You see eight isosceles right triangles in the picture with equal hypotenuse, which is indeed the side of octagon. All because of the internal angle of 1 3 5 = 9 0 + 4 5 degree for octagon.
Log in to reply
Thank you, now I got it. At first I didn't think of proving it via angles, and I thought of making a proof via comparing all the corresponding sides of two triangles.
This was my thought. The equal areas of the triangles in different positions probably deserved a few words of explanation. (And yes, your reasoning is correct.)
this is art
i'm just up voting on every one of your solutions. do u think i could be as good as u in..... 14 years? (i'm 10) :o)
eh i'm not sure:/ *if i'll be that good
The area of a regular polygon is 1/2ap and p=8s. Substitute and reduce to get A=4as.
The area of the red triangle is 1/2bh, b=s, and h=2a. Substitute and reduce to get A=as
Therefore the area of the entire octogon is 4 times the area of the red triangle. In other words the area of the triangle is 1/4 of the octogon.
This is how I did it!
The triangle connecting the base of the red triangle to the center of the octagon is 1/8 of the octagon. The red triangle has double its height, so it must have twice the area. It must cover 1/4 of the octagon.
Area of octagon = 1/2 (apothem) (perimeter)
Perimeter = 8s
So area = 1/2 (apothem) (8s) = 4as
Area of triangle = 1/2 bh
b = s
h = 2a
So, area = as
Therefore the area of the triangle is 1/4 of the area of the octagon.
When a = the apothem, and P = perimeter the Area of a polygon is
A p o l y g o n = 2 1 a P
The perimeter of a polygon when n = number of sides and s = side length is
P p o l y g o n = n s
Substitution yields
A p o l y g o n = 2 1 a n s
The area formula for a triangle is
A t r i a n g l e = 2 1 b h
Given that b = a side (/(s/) and /(h/) = two apothems /(a/) the equation becomes
A t r i a n g l e = 2 1 ( s ) ( 2 a )
Rearranging using the commutative property and removing the parentheses yields
A t r i a n g l e = 2 1 2 a s
So the fraction of the polygon that the triangle yields is
A p o l y g o n A t r i a n g l e = 2 1 a n s 2 1 2 a s
Reducing by canceling yields
A p o l y g o n A t r i a n g l e = n 2
Since we are dealing with an octagon n = 8 and the fraction becomes
A o c t a g o n A t r i a n g l e = 8 2
Reducing yields
A o c t a g o n A t r i a n g l e = 4 1
There are 8 triangles in a octagon. The red triangle takes up two triangles when cut, therefor is a 1/4 of the octagon
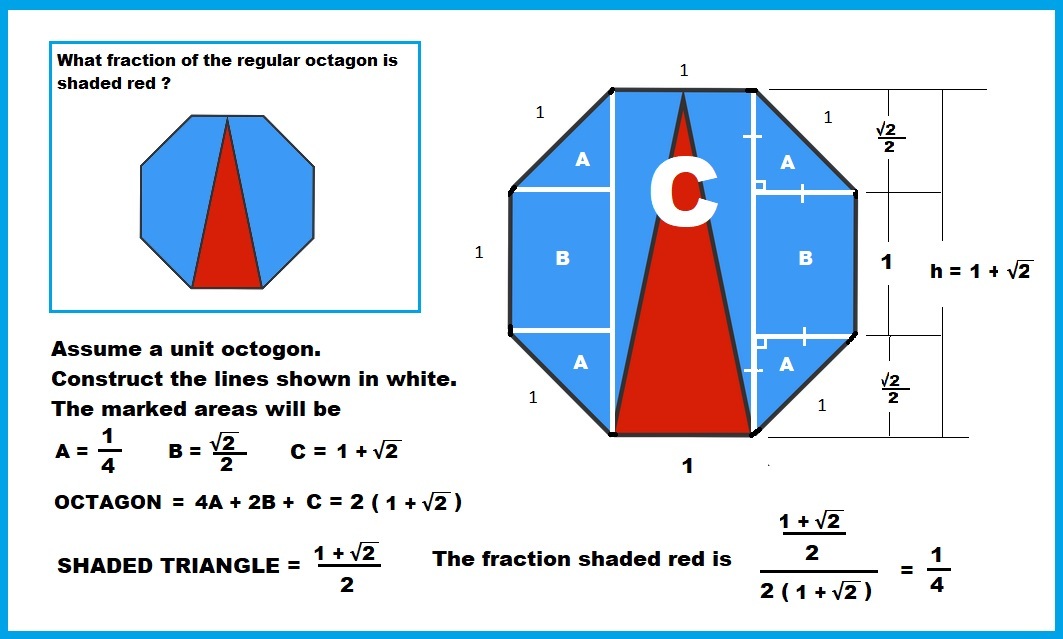
Given a side = 1 and the standard formula for calculation of the area of an octagon, extend a line completing the base of the octagon, then vertically to compute the height of the red triangle by solving for the sides of the 45 degree right triangle with hypotenuse 1, then after computing the area of the red triangle, dividing by the area of the octagon to determine fraction, thus =((1+2*0.5^0.5)/2)/4.83=0.249
Given the area of regular octagon as 2(1+ 2 ) a 2 , and using the angle formula for regular polygons = 1 8 0 − ( n 3 6 0 ) , a regular octagon has 1 4 5 ∘ inner angle, so that the when broken into 3 parts from the side edges, the height of the octagon or the triangle turns out to be a + 2 a + 2 a which is ( 1 + 2 ) a .... Calculating the area of the triangle using 1/2 X Base X Altitude, Triangle area = 2 ( 1 + 2 ) a 2 .... Thus the given area is 4 1 the original octagon area
LET THE LEGS OF THE ISOSCELES RIGHT TRIANGLE ON THE LOWER RIDHT CORNER OF THE FIGURE
BE Y, AND THE LENGTH OF EACH SIDE OF THE FIDURE BE X, THEN
X^2 = 2Y^2, X = SQRT(2)Y
THE AREA OF THE FIGURE IS
A = 2(2X + 2Y)Y/2 + X(X + 2Y) = 2XY + 2Y^2 + X2 + 2XY = 4SQRT(2)Y2 + 2Y^2 + 2Y^2 = 4( SQRT(2) + 1)Y2
THE AREA OF THE PINK TIANGLE IS:
B = X(X + 2Y)/2 = Y^2 + SQRT(2)Y^2 = (1 + SQRT(2))Y2
THEN
B/A = (1 + SQRT(2))/(4(SQRT(2) + 1) )= 1/4.
I am presenting a generalized solution which is not as elegant as the previous ones but could prove useful when you do not get any special insights to simplify the problem (Apologies if the presentation is a little clumsy in terms of mathematical notation)

The above also attempts to delve into the general properties of regular polygons

Triangle A B C has double the height of triangle A B O and the same base. It therefore has double the area, that is 4 1 of the area of the octagon.