35 of 100: Most People Don't Find Them All
How many triangles are there in this figure?
Beware: The triangles can be any size.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Clear and simple!
awwwww got dat 1 wrong :< waaaah!!!!!!
But you forgot about the largest triangle - the one whose two sides coincide with two adjacent sides of the square, there are four of them, so the total is 48!!!!!!!!!!!!!!!!!!!
Log in to reply
The largest triangles are counted this way, as the large triangles of the large square.
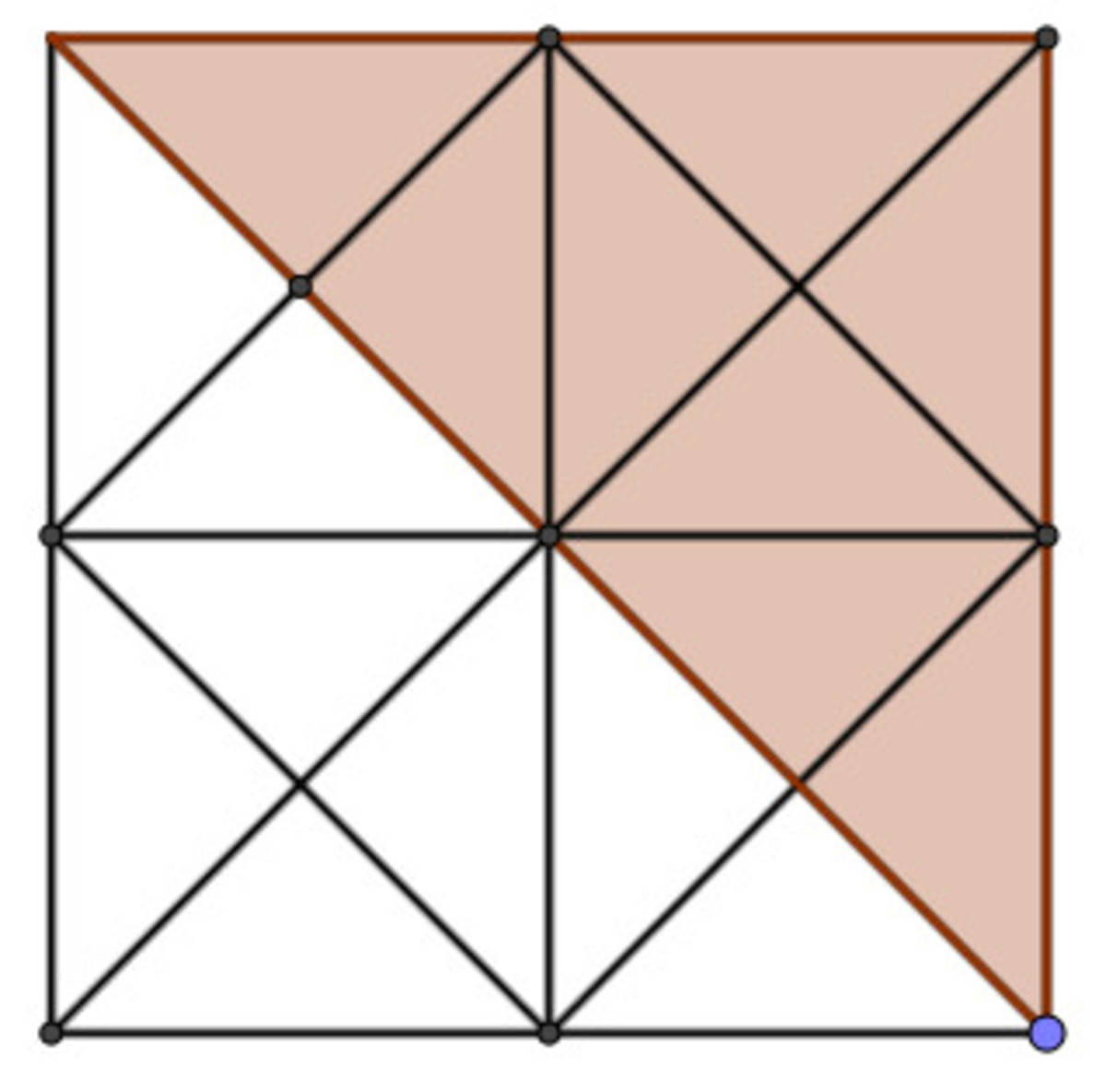
8 triangles that are only a given color. 4 colors. 32 single color triangles.
2 triangles that are red and orange. 4 neighboring color pairs. 8 two color triangles.
4 triangles that use three colors.
Total 44 triangles.
Great observation!
Nice use of casework!
16 single triangles
16 triangles made of two of those, there are 4 in each colored area.
8 triangles made of four of the simple ones, these take in two colored areas. The ones in the two areas which are side by side will have the longest side horizontal, either at the top or bottom, with the third vertex then down or up from there. Another four will be where the two areas are above each other, with the longest side of the triangle vertical, on the left or right.
4 triangles each made of 8 simple triangles. These will have a diagonal as their longest side and two sides of the overall triangle as legs. Either diagonal works and the third vertex can be either up or down from it.
I think there are two stages to solving this:
1) Find all the types of triangle
2) Count how many triangles there are of each type
To help with part (1), note that all of the triangles are right-angled isosceles triangles. [The smallest angle in the diagram is 4 5 ∘ and all of the other angles are multiples of 4 5 ∘ . The angles in a triangle add up to 1 8 0 ∘ , so the only way to do this is with 4 5 ∘ + 9 0 ∘ + 4 5 ∘ .]
A second observation is that the number of small triangles that makes up a bigger triangle is always a power of 2. [The side-lengths are either multiples of the side of the small triangle, or of the hypotenuse of the small triangle, which involves 2 ]
In the diagram below the smallest triangle is shown in yellow. There are 16 of these.

Putting 2 of the small triangles together forms this yellow triangle. The right angle of this triangle can appear in any of the four corners of the four coloured squares. This means there are 16 of these:
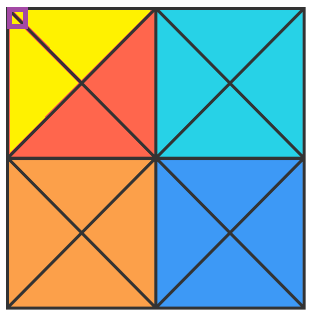
This yellow triangle is formed of 4 of the small ones. This time I have marked the places where the right angle of this triangle can go. There are 8 places, so there are 8 of these triangles:
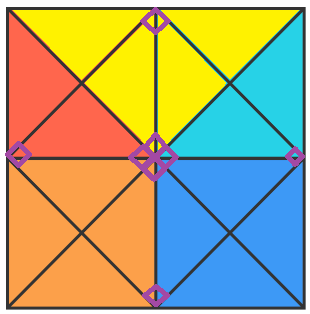
Finally there are triangles that are 8 of the small ones. There are 4 of these:
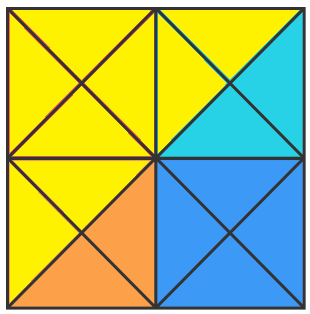
In total there are 1 6 + 1 6 + 8 + 4 = 4 4 triangles of different sizes.
... that's exactly how I solved this problem. I think your solution was explained with good precision.
I was "lazy" and tried to solve the problem subtracting the number of degenerate triangles from the binomial (13 over 3). However I couldn't get the right answer, and would like to know hot to solve the problem this way correctly.
Log in to reply
... look at the diagonal of the overall square. The diagonal is composed of 4 congruent line segments. These are the "shortest" line segments in this figure, so we can arbitrarily assign them a length of 1. These line segments are also the legs of 1-1-√2 right triangles. So total up the number of 1-1-√2 right triangles: 16. Next, total up the number of √2-√2-2 right triangles. Some will be pointing northeast-southwest and some will be pointing northwest-southeast. Again there are a total of 16. Next total up the number of 2-2-2√2 right triangles. There are two of these in each horizontal or vertical half of the overall square. They are pointing east or west or north or south. This time there is a total of 8 2-2-2√2 right triangles. Finally, total up the number of 2√2-2√2-4 right triangles. These are the triangles that have a diagonal of the overall square as their hypotenuse. There are four of these triangles (i.e. each corner of the overall square is the right angle of one of these triangles). Total up the four sizes of 45˚-45˚-90˚ triangles and you get 16 + 16 + 8 + 4 = 44.
Log in to reply
Thank you, however I wanted to know if it's possible to solve the problem using binomial coefficients in an effective.
Log in to reply
@Gabriele Manganelli – ... so sorry, I misread your comment. I think your issue boils down to how you define a set and then who joins that set. If you think of the right angles of the triangles in this task as "pointing" in one of eight possible directions, you can ask questions like "how many triangles are pointing directly north?" For each of the directions north, east, south and west, there are 6 triangles pointing in that direction. For each of the diagonal directions NE, SE, SW and NW there are 5 triangles. However, I'm not sure what effectives these tasks might belong to ...
I solve these puzzles in the most boring possible way using a graph based algorithm. The edges of the graph are pairs of nodes that connect in a straight line regardless of intervening intersections.
With this method there is no dependency on the overall shape, triangular, rectangular grid, etc. found in these puzzles.
[Aside: I was not impressed with the presentation in the style of click bait "most people ...", "only x% of people .." Suggested title "Hot Cross Boxes" ]
2017 July 9 Computer implementation. There is one subtlety, the orientation of each edge must be noted in order to detect when two edges connect into a single line not two independent sides of a triangle. No change in orientation, no triangle. Apart from that the edge to straight line mapping and ordered search for circuits in increasing node index method in code gets the correct count.
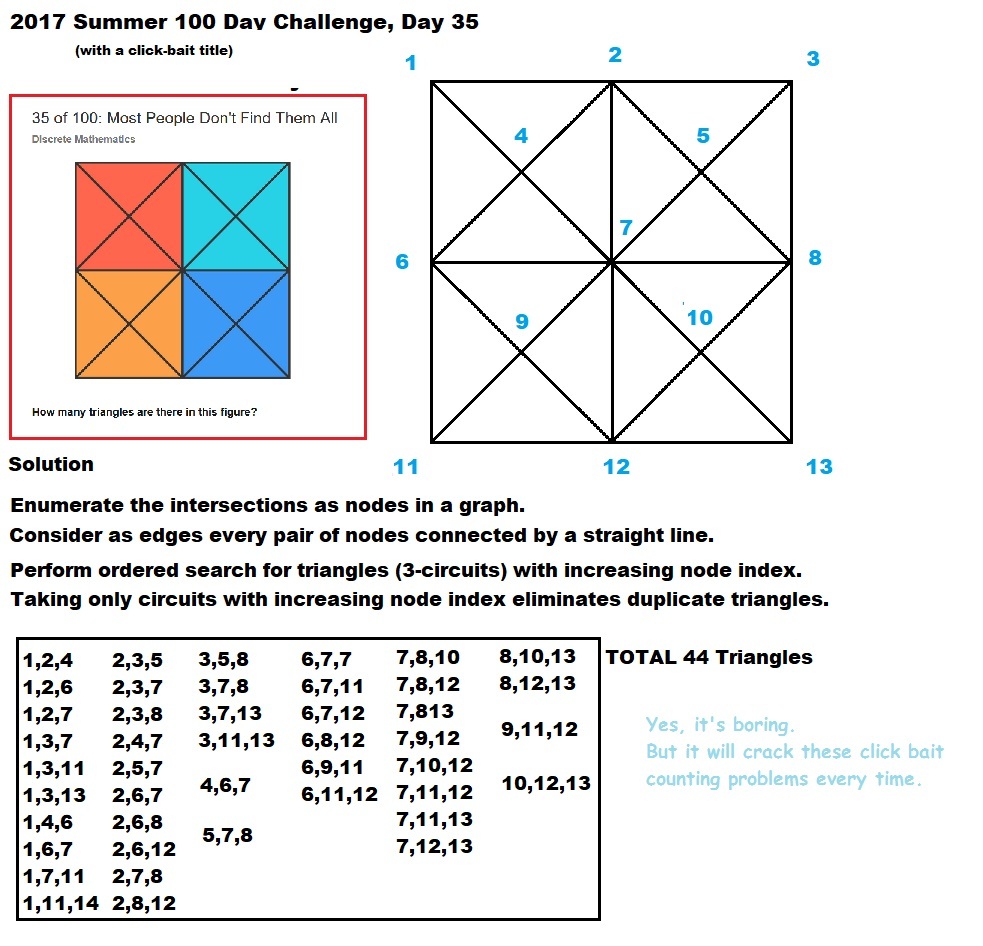
I like the brutality of it. And of course the generality.
How did you make this? Is it part of the graph? Also, did you write the algorithm?
Log in to reply
The diagram was made with MS Paint and Snipping Tool (to get the original site diagram) on a WIn10 PC. One might say I wrote the algorithm in as much as I did not copy it from elsewhere. I applied ideas I had acquired by study or work experience in IT, thus standing on the shoulders of reasonably tall persons if not giants.
... I've never seen this formula before. I would like to derive it so that I can understand the significance of each term (... i.e. why 18*n^3, etc. ...). Thanks.
Log in to reply
Please search for the number sequence "A100583".
How to derive formula please explain
Log in to reply
Check the link: https://divisbyzero.com/2011/02/10/counting-triangles-on-a-tin-ceiling-solution-2/
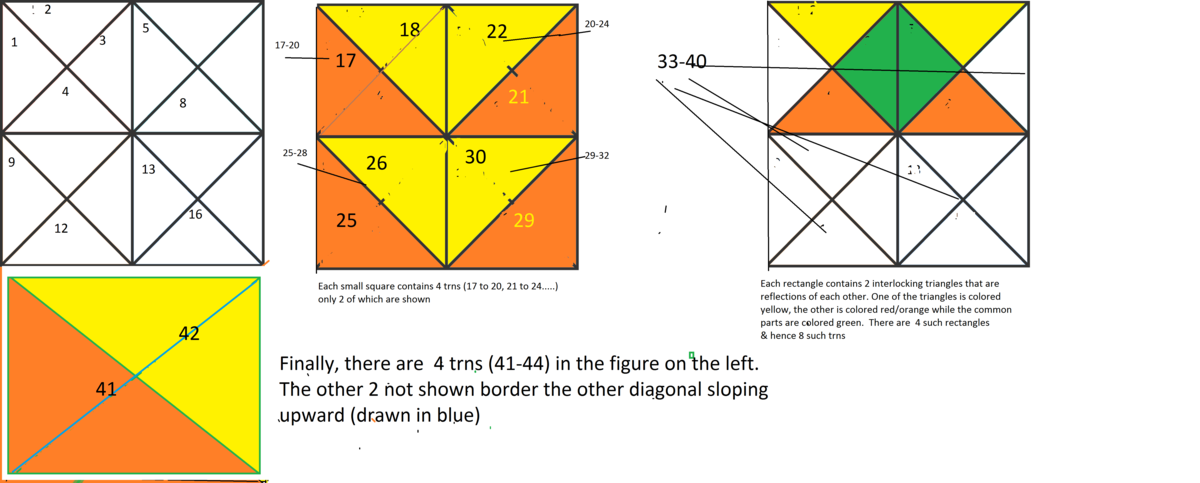
This is my solution.
The pictures are self-explanatory.
Count the squares. In each square there is 8 triangles, plus 12 combinations.
16 of
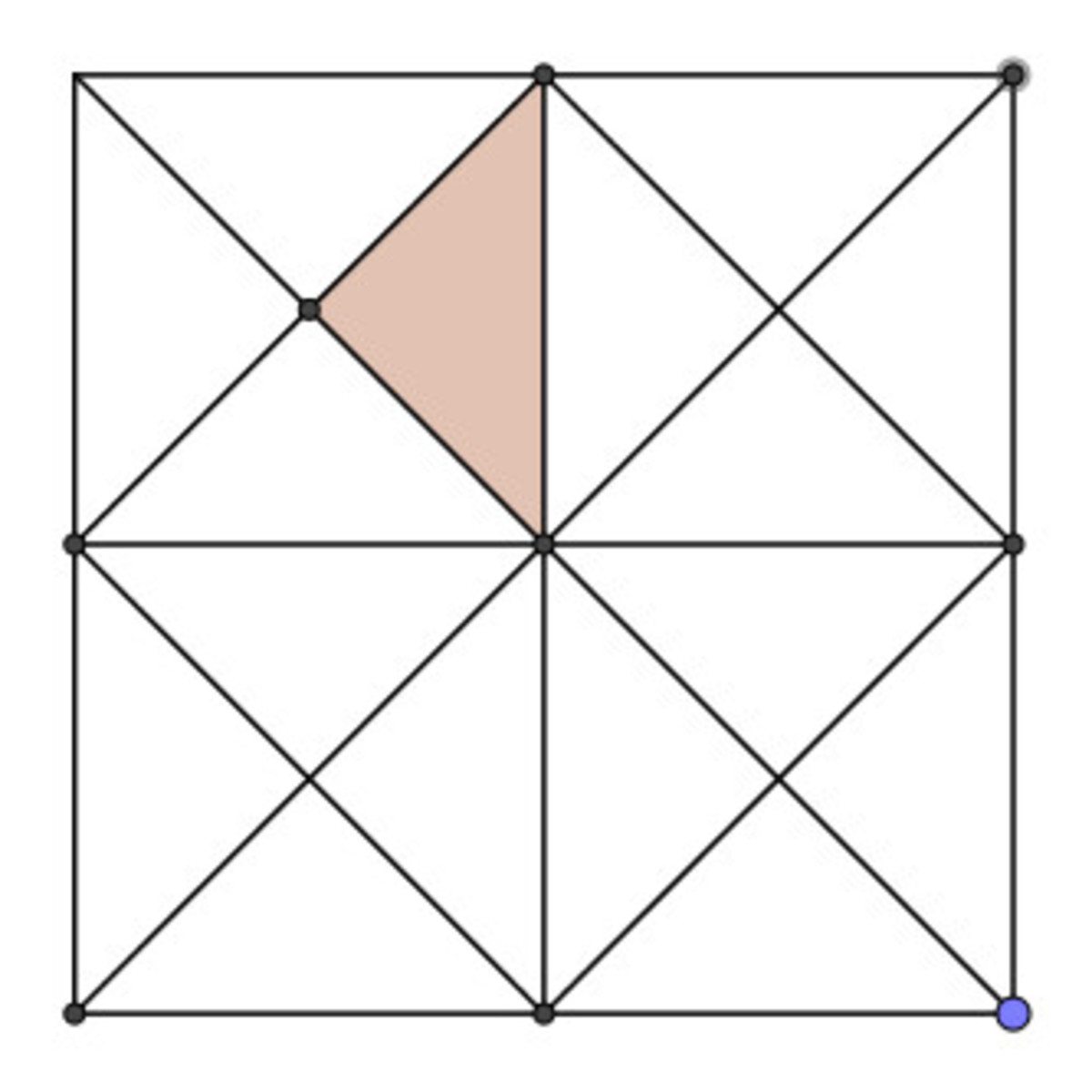 16 of
16 of
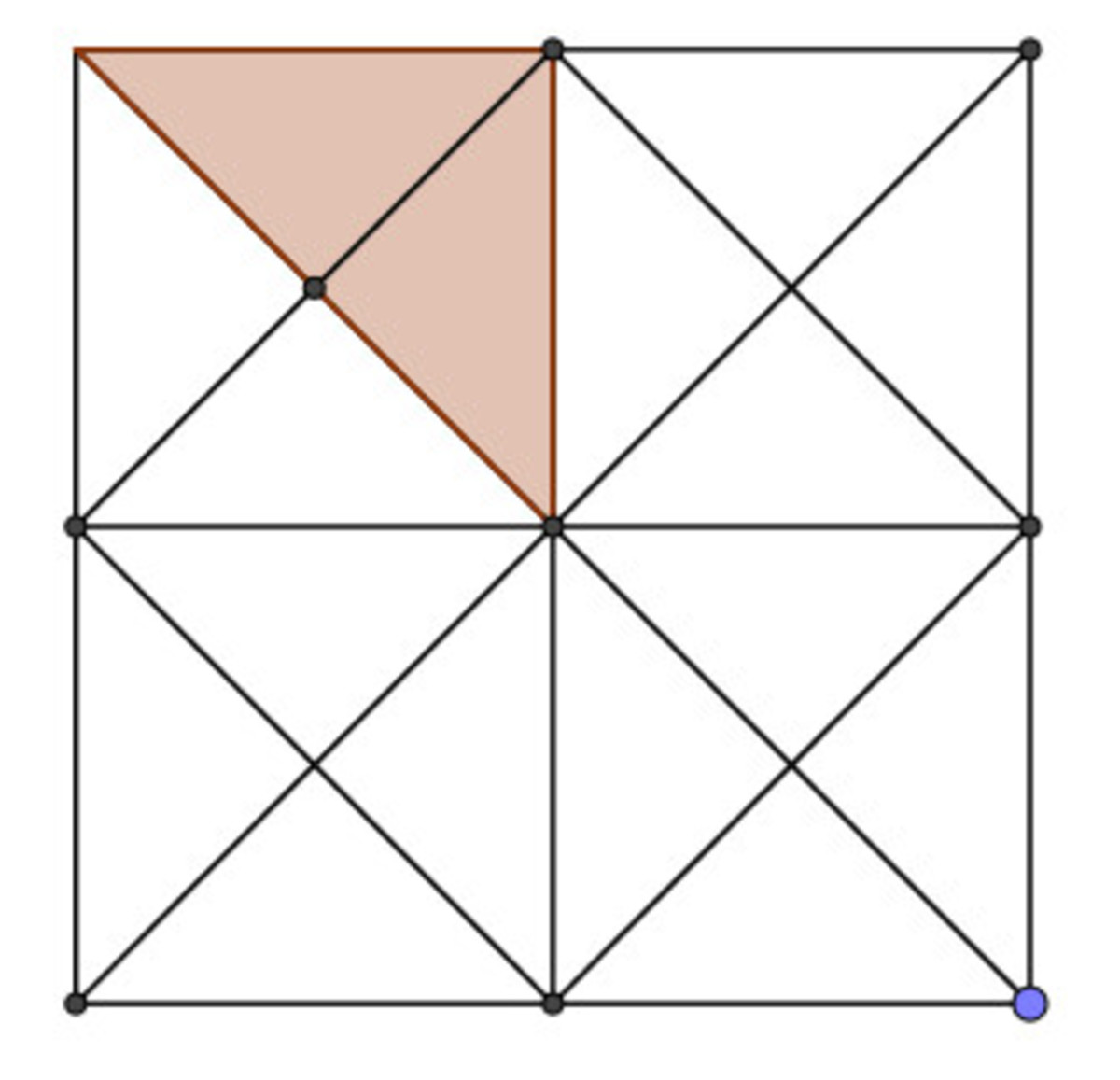 4 of
4 of
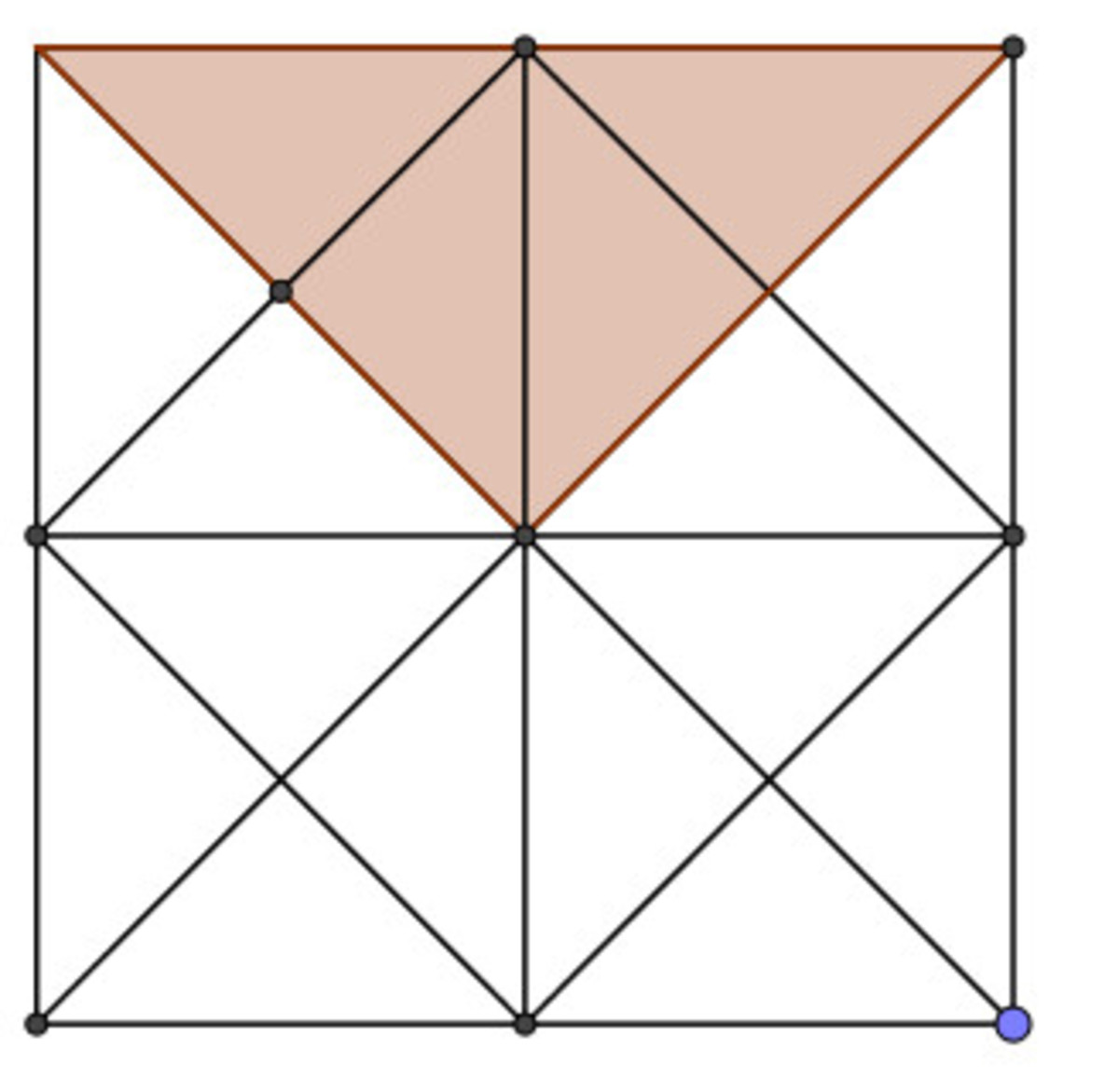 4 of
4 of
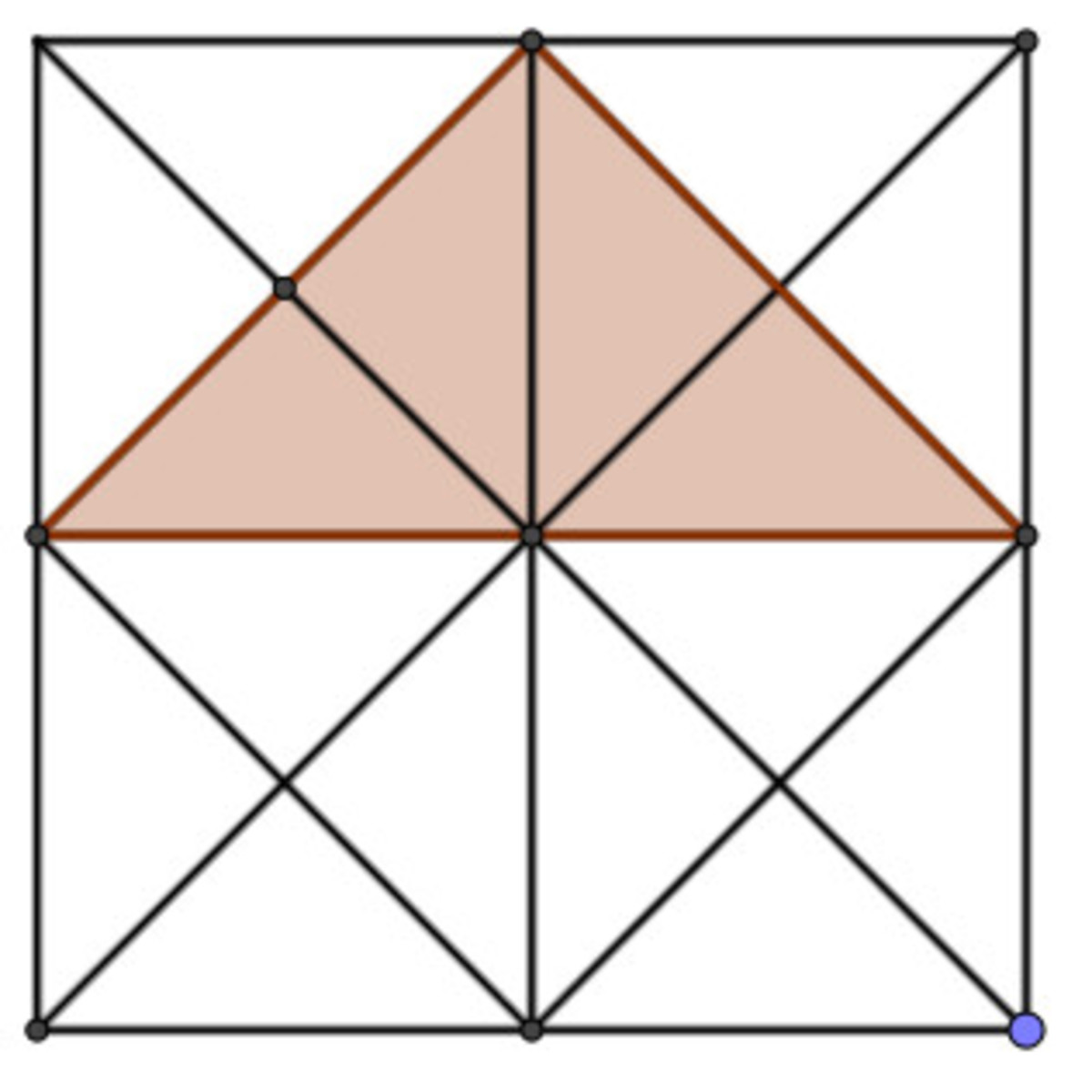 4 of
4 of
Total: 44
Solved it by SHEER LUCK.
By counting, l obtained this:
1 6 + ( 8 × 2 ) + ( 4 × 2 ) + ( 1 × 2 ) + ( 1 × 2 ) = 4 4

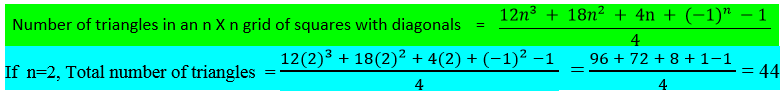
There are 6 squares in the original picture (four small, one medium and one large). If we take out each square like the picture above, then each square contains 8 triangles (four small and four large, where each large one consists of two small ones). But 4 of small triangles of the medium square are counted twice this way (once as smaller triangles of itself and once as larger triangles of small squares).
Thus in total we have 6 × 8 − 4 = 4 4 triangles.