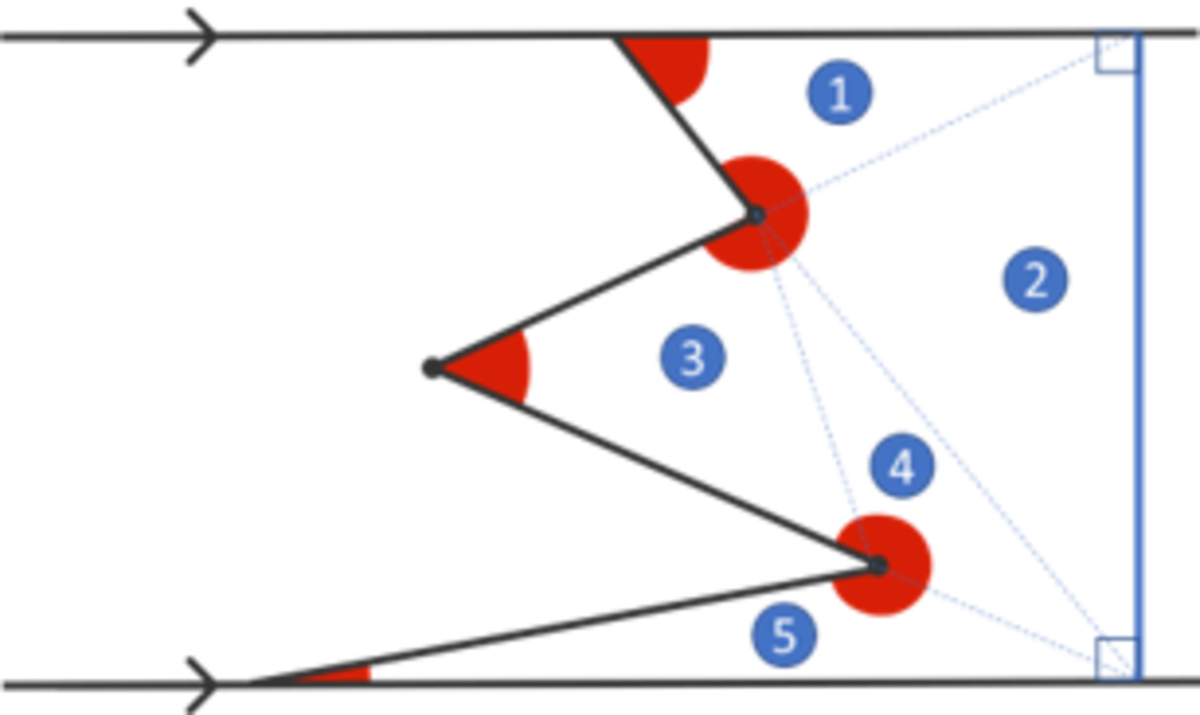
41 of 100: Zigzag
What is the sum of the red angles?
As typical for a geometry problem, adding line segments might help! There are a few approaches this time though.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
that is exactly how I did - it is the most easiest method I guess
Draw parallel lines through the points inside the two parallel lines.
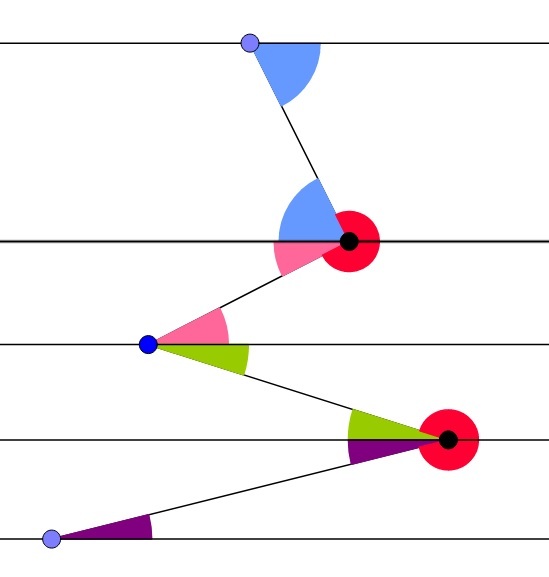
Hence around each of the two balck points there are 3 6 0 ° degrees. Therefore the sum is equal to 2 ∗ 3 6 0 ° = 7 2 0 ° .
An other completion of my solutin (by @John Young ):
After you draw the parallel lines each pair of red angles between the parallel lines add up to 1 8 0 ° . So 4 ∗ 1 8 0 ° = 7 2 0 ° .
After you draw the parallel lines each pair of red angles between the parallel lines add up to 180. So 4 * 180 = 720
Log in to reply
Interesting note, thanks! I mention it in my solution.
Relevant wiki: Parallel Lines (Geometry)
The interior angles on the same side of each adjacent pair of parallel lines add up to 180.
4 × 1 8 0 = 7 2 0

I like your solution the best. The subproblems are simple and identical. It generalizes, and can be applied quickly, to larger versions of this problem with any number of "zig-zags".
awesome picture
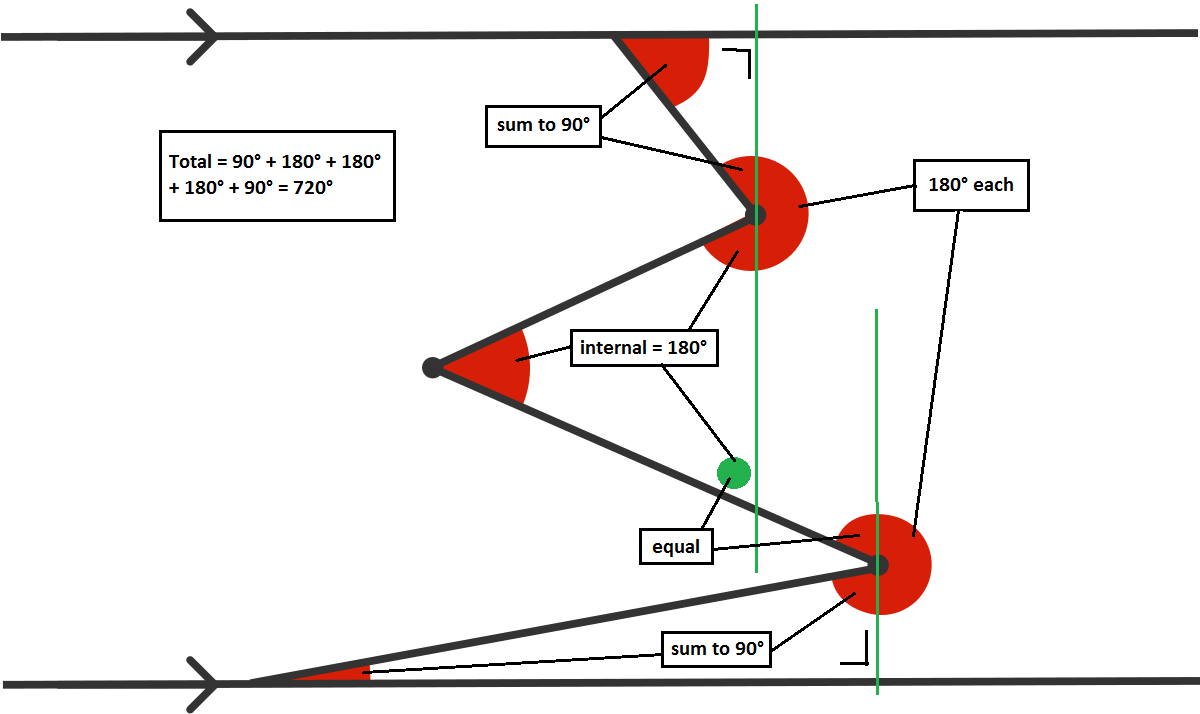
With similar logic, we can also draw a vertical line perpendicular to the parallel lines on the left side. This would create two shapes (one on the left and one on the right), both with the same number of sides and thus both with the same sum of their interior angles. Two of those angles in each shape would be right angles, given that lines were drawn perpendicular to the parallel lines. As a result, we can conclude that the sum of the remaining angles in each shape are equal to each other. That is, the sum of the angles on the left side of this path connecting the top and bottom parallel lines is equal to the sum of the angles on the right side. This may come somewhat intuitively, and is true for any path between two parallel lines made out of line segments.
Since we notice that the problem is only asking for the sum of the angles on the right side of the path, we know it must be half of the total sum of all angles along the path on either side. So, considering both the left and right sides of the path, the sum of all angles is 1 8 0 ∘ + 3 6 0 ∘ + 3 6 0 ∘ + 3 6 0 ∘ + 1 8 0 ∘ = 1 4 4 0 ∘ , with the 1 8 0 ∘ angles coming from where the path intersects each of the parallel lines and the 3 6 0 ∘ angles coming from each turn in the path. We are only looking for the sum of the angles on the right side, which is half of the sum of all angles, so we simply do 1 4 4 0 ∘ ÷ 2 = 7 2 0 ∘ to get what we are looking for: the sum of the red angles.
This can easily be generalized for whenever we are looking for the sum of all angles on one side of a path made out of line segments between and connecting to two parallel line. In that case, let n be the number of line segments the path is made out of. In this scenario, for the total angle sum there would be n − 1 turns in the path of 3 6 0 ∘ each and always two endpoints of 1 8 0 ∘ each that sum to 3 6 0 ∘ . Therefore, the sum of the angles on one side of the path would be 2 3 6 0 + 3 6 0 ( n − 1 ) ∘ = 2 3 6 0 n ∘ = 1 8 0 n ∘ .
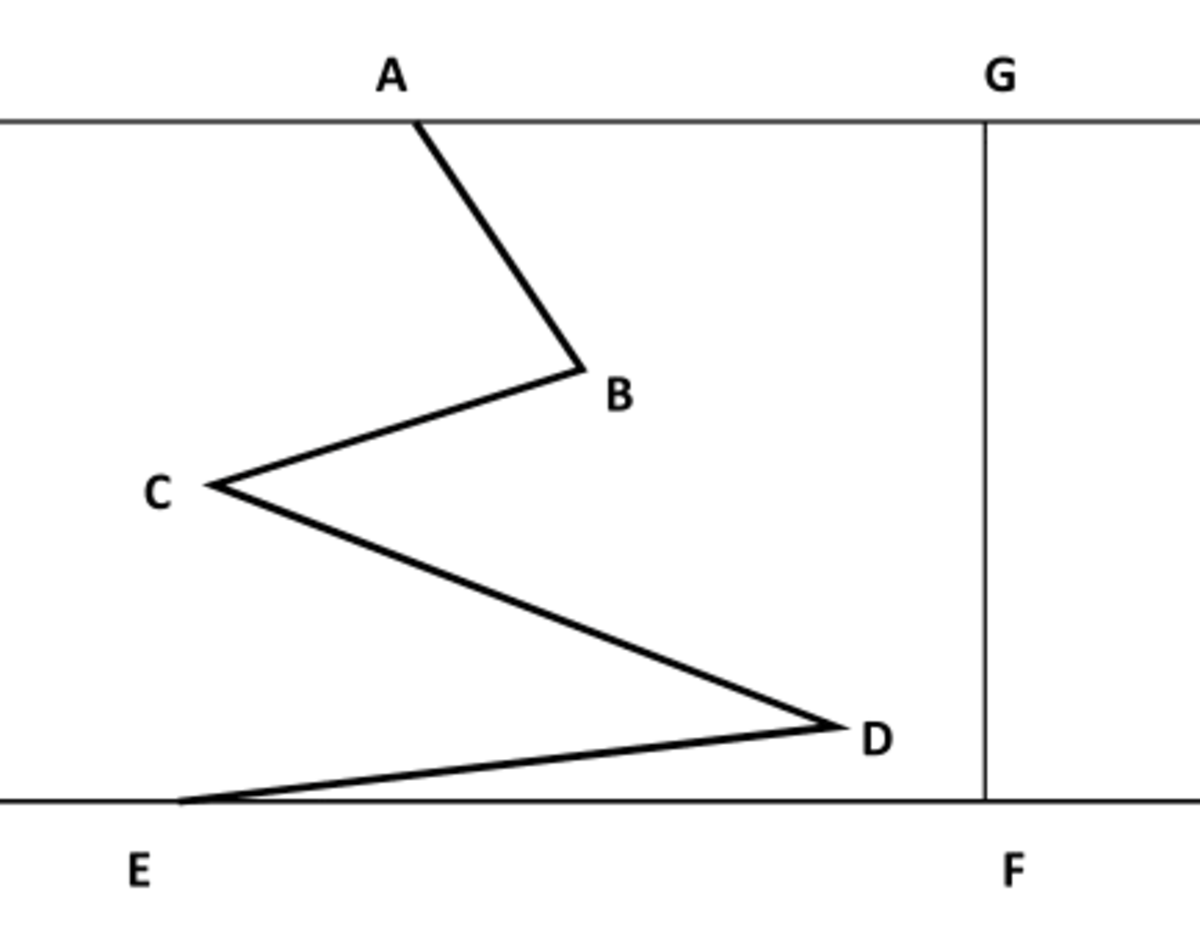 The polygon ABCDEFG has 7 sides, therefore the sum of its internal angles is
9
0
0
∘
.
The polygon ABCDEFG has 7 sides, therefore the sum of its internal angles is
9
0
0
∘
.
To get the desired sum the two right angles at F and G need to be subtracted.
The answer is 9 0 0 ∘ − 2 × 9 0 ∘ − 7 2 0 ∘
I had this solution showing before, and had a number of upvotes. Then it was taken down. I don't know why. I don't see anything wrong with it.
I figured 4 180 reversals equals 720.
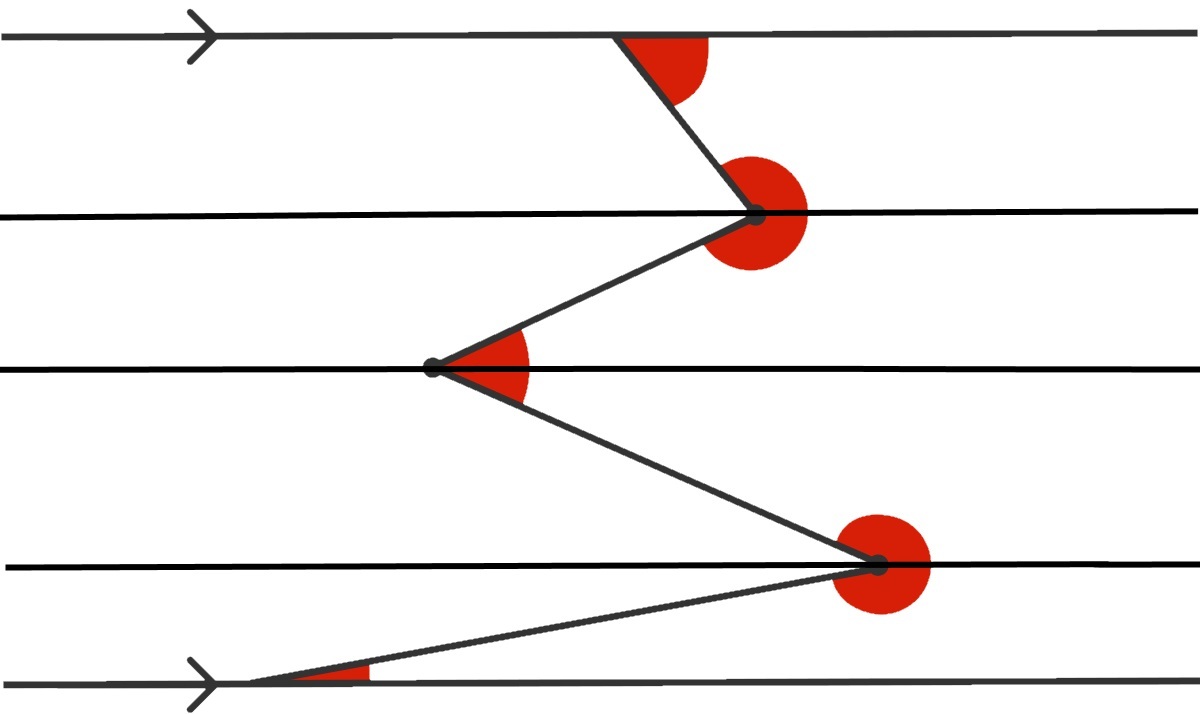 If we draw three parallel lines through the mid-points of each angle, we see the supplementary angles between them. This is possible because the red angles are drawn in an inside-outside pattern. Now, all we have to do is count the pairs. As you can see, there are 4 pairs. So, 4 pairs x 180 degrees/pair=720 degrees for all the red angles. ☺☺☺☺
If we draw three parallel lines through the mid-points of each angle, we see the supplementary angles between them. This is possible because the red angles are drawn in an inside-outside pattern. Now, all we have to do is count the pairs. As you can see, there are 4 pairs. So, 4 pairs x 180 degrees/pair=720 degrees for all the red angles. ☺☺☺☺
Imagine adding extra parallel lines through each angle (there should be a total of 3 new lines or 4 gaps). By parallel postulate, each gap is 180°. Since there are 4 gaps, the total is 720°.
I suppose it would be interesting but obviously more difficult to generalize to the sum of angles on curved surfaces such as spheres. The sum of the angles in a triangle would obviously depend on the curvature (Of course , the latter would be uniform in a sphere)
Log in to reply
The horizontal and vertical lines would obviously correspond to the latitudes and longitudes (or vice-versa). The intersections of the sets of lines would still be orthogonal but i suppose the sum of the angles in each triangle would be less than 180, the deficit in each triangle depending on the curvature. But the question is would we have the same number of triangles ? Would all of them satisfy the triangle inequality (obviously with a metric adapted to spherical geometry) ?
Log in to reply
Sorry, the sum of the angles would be > 180 , not < 180
As mathematically impure as it is, there is only one plausible answer from looking at the diagram.
Consider a situation where you 'straighten' this diagram so that it is a straight line segment perpendicular between two lines with three nodes. In this case, the sum of angles would be 90 + 180 + 180 + 180 + 90 = 720. If we assume a Euclidean space, the act of 'straightening' the zigzag does not change the sum of angles. Thus the sum of angles in the zigzag is 720 degrees.
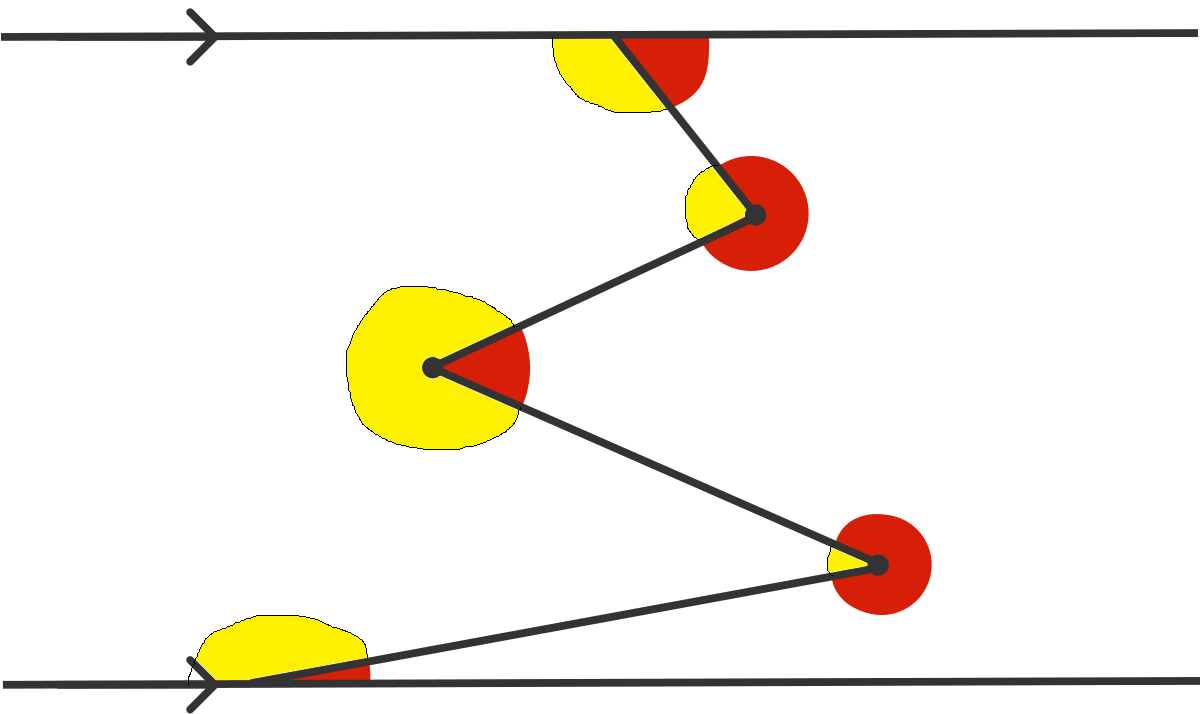
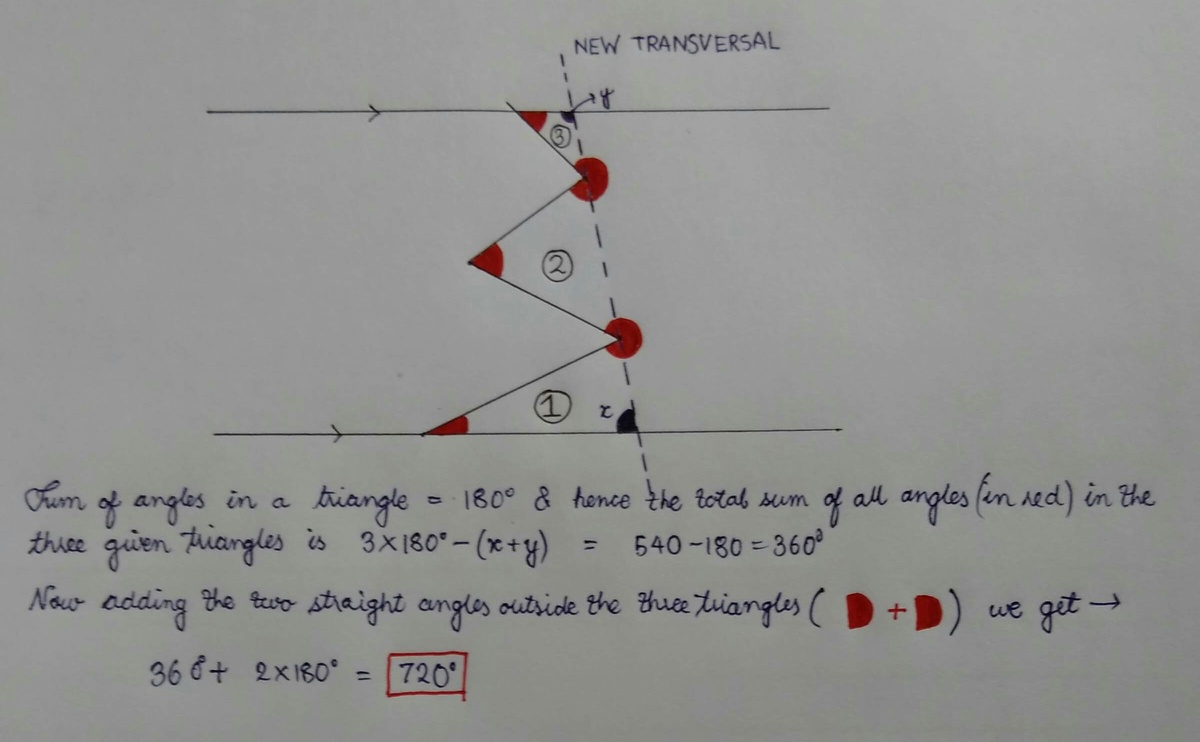
We have a theorem that says that the sum of the yellow angles in the figure is the same as the sum of the red angles. We can prove it by using theorems about two parallel lines with a transversal line between them. In Portuguese we call it as "Teorema dos Bicos", something like "Beak Theorem". For some reason I didn't find the correct name for this theorem in English. If somebody know what I'm talking about, please tell to me.
As I said, this this theorem sets that the sum of the yellow angles is the same of the red angles. If we sum all the angles we will have 1 8 0 ° + 3 6 0 ° + 3 6 0 ° + 3 6 0 ° + 1 8 0 ° = 1 4 4 0 ° . Dividing it by 2 we get 2 1 4 4 0 ° = 7 2 0 ° .
Create a heptagon (7-gon) by drawing a transversal perpendicular to the parallel lines.The sum of interior angles of any
n
-gon is
(
n
−
2
)
⋅
1
8
0
∘
. This is shown for the heptagon by dividing it into
n
=
5
triangles, where the interior angles of each triangle sum to
1
8
0
∘
. The total measure of the red angles is the heptagon interior angle total less the two right angles:
5
⋅
1
8
0
∘
−
2
⋅
9
0
∘
=
4
⋅
1
8
0
∘
=
7
2
0
∘
.
720 is the solution only if you assume the two lines are parallel ... so given that the lines are parallel is NOT stated then the correct solution is "There isn't enough information to determine".
Cant explain in words. Its just a brain logic. If you don't know adjustment then this problem is impossible. Just try to assume a proper circle which is of 360 deg. and try to use an logic of obtuse and acute so just adjust like I did. First red spot I consider a part of angle of equilateral triangle i.e 60 deg. Next red spot Is a obtuse angle and more than a semi circle but not a complete circle so it must be 360>x>180 so x can be as per assumption somewhat 290 deg. Next red spot is a acute angle so it is less than 90 deg. May be 50 deg. Next red spot is almost same as above obtuse theory so its around 310 deg. Next red spot Is as given in option 720 deg. so I consider that as 10 deg. So as per my Calculation 60+290+50+310+10= 720 deg.
Add a line perpendicular to the parallel lines on the right, making a heptagon with all red angles inside of it. Calculate the sum of angles for a heptagon to 900°. Substract the two overcounted right angles, ending up with 720°.
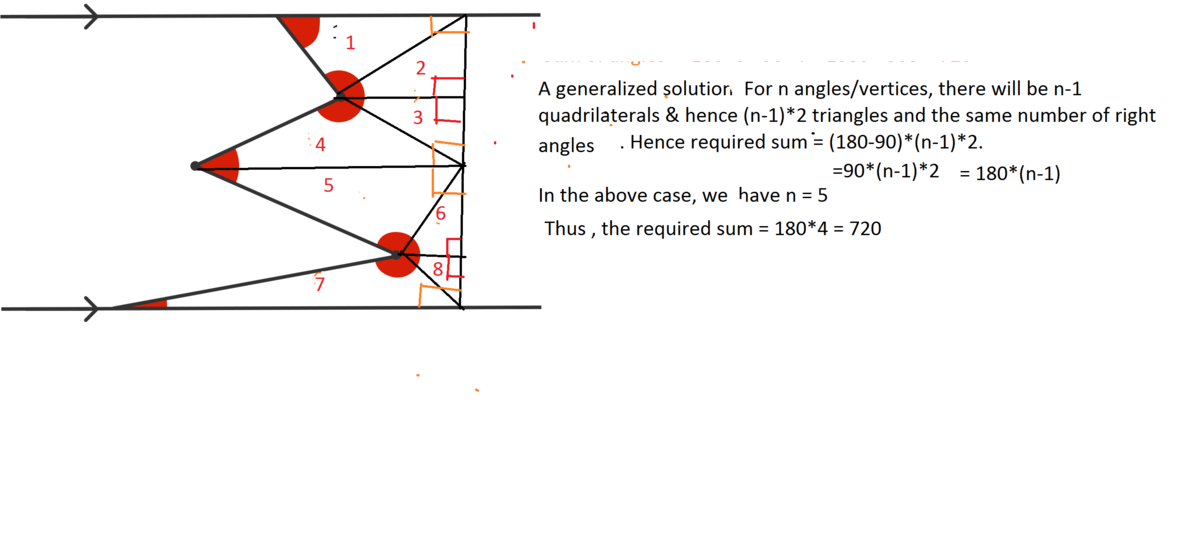
Draw one vertical line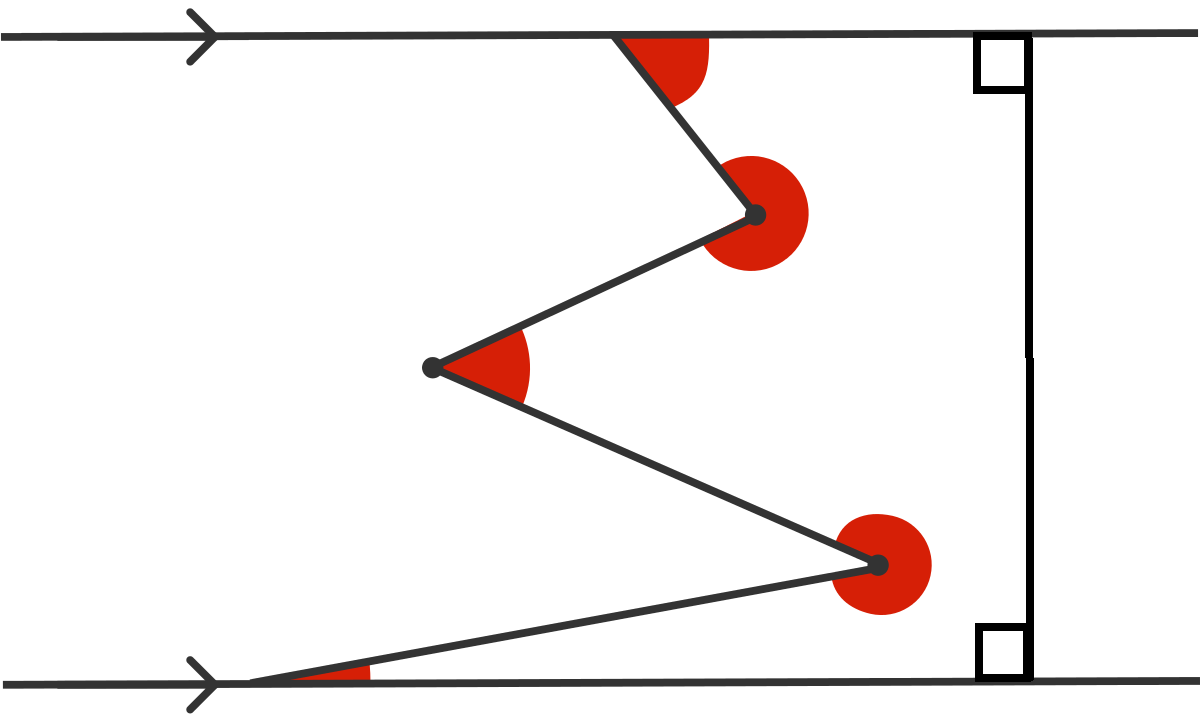 Because the figure above has seven sides, we use 7(180) - 360, and then subtract the extra 180 degrees from the right angles.
Because the figure above has seven sides, we use 7(180) - 360, and then subtract the extra 180 degrees from the right angles.