44 of 100: Semitricky Semicircles
What is the pink area in square units?
The figure shows 2 semicircles whose diameters are on the same line; the chord of length 24 units in the larger semicircle is tangent to the smaller semicircle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
The interesting thing to me is that the area is the same for all r>0 i.e when r is nearly 0 and R is just over 12 all the way to r<R<infinity.
Log in to reply
That is what makes the problem so appealing to me too.
Great solution!
I see that all of the diagrams are based on the assumption that the chord is parallel to the diameter of the circles. What words in the question substantiates this assumption?
Log in to reply
The little arrowhead on the two lines means that they are parallel.
The tangent to the smaller circle is perpendicular to a line segment from the center. So it be parallel to the shared diameter.
Log in to reply
I am not sure I follow this explanation at all. What would be a "line segment from the center"? And if it were a vertical line from the center, why would the tangent to the small circle be perpendicular to it?
The explanation below, about little arrows showing parallelism, is in my opinion superior to this one.
Log in to reply
@Marta Reece – My apologies. I don't think my reasoning was very strong; I was inferring from the shape rather than providing any proof. This is my faulty reasoning. If you draw a line perpendicular to the shared diameter from the center of the smaller circle to the chord which is a tangent, it would be at 90 degrees to the chord. Now since the internal angles sum up to 180 degrees, it implies that the two lines are parallel to each other.
But it does bring up an obvious question, what if they are not parallel? What if the chord and diameter if extended, intersect? Thanks for raising this.
Same as what I did
Nicely done.....
Very nice!
I don't understand how these pink areas in these 3 semicircles have the same sizes.
Log in to reply
As the outside semicircle gets larger, the amount taken out by the inside semicircle increases at the same rate. The solution shows why the rate is the same.
Assuming that the chord length remains 24, the size of each semicircle varies but the pink area does not due to the relationship between R, r, and the chord length
Look at Danny Whittaker's desmos graph. I didn't understand it either because the three examples all appear to be the same size. His graph explains it much better.
Very simple solution without the depth of proof.
Note 1: We aren't given any information about the size of the smaller circle. Note 2: There isn't an option of "Not enough information".
Conclusion: Area of pink region must be independent of size of small circle.
Let the small circle have radius of zero.
Area of the pink region is simply the area of a semi-circle with radius 12: 72pi.
I also created a graph on desmos to justify that the area is independent.
Nice idea, but it would be even nicer of you didn't take the problem creators' word for notes 1 and 2. I wonder how one might deduce those facts otherwise.
Engineer thinking :) Don't get me wrong, this is how I "solved" it, too!
Log in to reply
Yes, engineering thinking is more than maths and more than science. Its the learnt history both personal and public, common sense, experience from solving similar problems and the common connection between dissimilar problems.
Wonderful! I also thought the lack of information meant the answer didn't depend on specific radii, so I just picked a pretty Pythagorean triple like 9-12-15 (small radius, half of chord, large radius) and computed areas that way.
Doing questions like this is always so satisfying
This solution is 100% valid, and clever. Of course we "take the problem creators' word" - how could we ever solve a problem if we didn't?
Log in to reply
I write reports on problems which are faulty in one way or another far too frequently to just believe and leave it at that.
There is always a nicer way!
In order to calculate the area of the shaded portion, you would need to know the size of the smaller semicircle in relation to the larger one. Since the smaller semicircle can be made larger or smaller, the shaded area will become less or greater in response. For example if the diameter of the larger semicircle were held at 30, all five answers can be obtained by making the smaller semicircle have a radius of sqrt(153), sqrt(145), sqrt(129), sqrt(113), and sqrt(81). Choose any number for the diameter of the larger semicircle greater than 24, which must be less than the diameter, and you can find any given solution for the area of the shaded part. If R is the radius of the larger semicircle, and the area is B pi, then the radius of the smaller circle will be sqrt(R^2-2 B).
Log in to reply
Not true. The cord has to be 24 and has to be tangent to the small semicircle at its highest point. To do that in a larger outer circle, the inner circle has to be quite large. For any size of larger circle, the size of the smaller one is determined by the location of the cord.
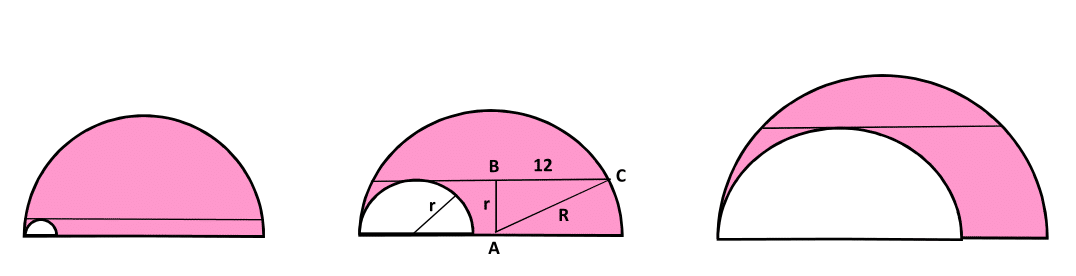
Log in to reply
You're right. I didn't hold the chord length as the constant. Basic mistake.
This is not actually solving the problem, this is finding an answer by hoping the problem was written perfectly. Problems selected for the summer specials generally are, other problems may not be.
Log in to reply
This is a solution. The amount of information given indicates that the size of the smaller semicircle doesn't matter. If it did matter, the problem would be underdetermined and unsolvable. The only options are "written perfectly" and "unsolvable", so there's nothing wrong with assuming it is.
Log in to reply
It is still a reverse engineering. You use the options given to find the answer, not the statement of the problem alone.
Log in to reply
@Marta Reece – I used a similar solution without looking at the options at all. The solution must be independent of the smaller radius, you can call it "reverse engineering" if you like, but it's simply math.
A lot of problem-solving (esp. in test-taking situations) is based on the presumption that the question is written properly. Using the logic of taking progressively smaller circles it becomes easy to prove that 72pi is the only possible answer.
Log in to reply
There are many types of problem solving in test-taking situations.
Denote the radius of the small semicircle
r
and the radius of the large semicircle
R
. Create a diagram similar to this:
Set the equation up as r 2 + 1 2 2 = R 2
The area of the pink region is the area of the large semicircle subtracted by the area of the smaller smeicircle. In other words, 2 π R 2 - 2 π r 2 or 2 π ( R 2 − r 2 ) .
Using the first equation, R 2 − r 2 = 1 2 2 = 1 4 4
The area of the pink region is 2 π ( 1 4 4 ) = 72π
Edit: I apologize for the hand drawn figure, I don't know how to make good images like those in the solutions above.
It's fine! Thanks for explaining it clearly!
@Kevin Guo - It's clear, and any clearly-explained solution is a good solution! If you want to experiment with figures, you could try Powerpoint: copy and paste the problem figure image into a blank Powerpoint slide, draw whatever additions to it you want, select the entire drawing , and right click to "Save as Picture...". Once saved, you now have a *.png you can upload into your solution. FYI, this can be improved on, e.g., to make the picture smaller, but the above are the basic steps. Maybe others can share their figure methods... Hope this helps!
Thanks @William Huang and @Wesley Zumino for your feedback!
Log in to reply
I do my drawings using Microsoft Word. I then print them, use PDFtoPNG.com to get a picture file, which I clip to desirable size using Paint. It seems like a lot of steps, but they are just click, click, click. And except for Word, all the programs are free downloads.
I much prefer hand drawn solutions. Actually, I think students prefer them too. I wonder if there is research on my hypothesis that are brains are wired to understand hand drawn explanations first and then use technology to reinforce the learning?
Desmos demo
A demonstration in desmos that the area of the shaded region doesn't change as the size of the semicircles change. Click on link. Drag purple dot.

Lazy solution
Apparently, the answer does not depend on how big or small the white semicircle is.
Let's shrink it down to size zero. Then the chord of length 24 has the same length as the diameter of the pink circle. Thus its radius is 12, and the pink area is half the area of a circle, A = 2 1 ⋅ π ( 1 2 ) 2 = 7 2 π .
Coordinate solution
Let the center of the pink semicircle by at ( 0 , 0 ) and its radius R ; the white semicircle has radius r . The chord connects the points ( ± 1 2 , r ) . Since these points lie on the pink semicircle, 1 2 2 + r 2 = R 2 ∴ R 2 − r 2 = 1 2 2 . Now the pink area is 2 1 π R 2 − 2 1 π r 2 = 2 1 π ( R 2 − r 2 ) = 2 1 π ( 1 2 2 ) = 7 2 π .

Let, radius of small circle is r and radius of large circle is c , So, area of white portion is 2 π r 2 , From the triangle we can write c 2 = 1 2 2 + r 2 , Now, Area of pink portion is = 2 π c 2 − 2 π r 2 = 2 1 4 4 π + 2 π r 2 − 2 π r 2 = 7 2 π
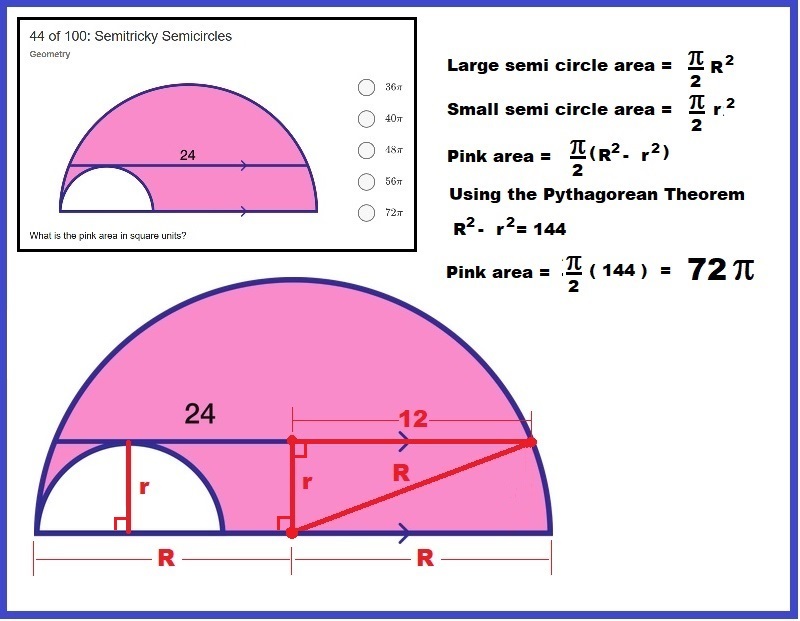
Compare to an earlier problem.

I have cheated slightly. :) Note that the configuration isn't unique - if we increase the radius of the big circle and move the horizontal line up so it stays at 24 units, it should still give the same answer. So consider the limit as the small circle's radius tends to zero. Then the diameter of the big circle would be 24 as the chord would be the same as the diameter. So the answer would be 2 π × 1 2 2 .
It reminds me of a similar Gardner problem about a sphere with a hole.
Assuming that there is an exact solution, it does not depend on the radiuses of the two circles. So, if the smaller circle is infinetely small, the solution is the area of a semicircle with radius 12.
Using logic:
Let the radius of the small and large semi-circles be r and R respectively.
The problem statement implies that the value of r/R does not affect the pink area.
As r tends to zero, R tends to 12, so the pink area tends to 2 1 × π R 2 which equals 7 2 π
suppose, radius of the bigger semicircle is R and the radius of the smaller semicircle is r.
so, It can be observed that R^2=12x12-r^2. => R^2=144-r^2.
So, pink area=(1/2)pi(R^2-r^2)=(1/2)pie144=72*pie
Solution as per intersecting chord theorem.
Let the radii of large and small circles be R and r. Draw a diameter in the large circle, perpendicular to the chord of length 24, bisecting it in two segments of lengths 12 & 12.
The intersecting chord would cut the diameter into two segments of lengths (R+r) and (R-r).
As per intersecting chord theorem, the product of the segments of intersecting chords are equal.
So we have, 12×12 = (R+r)(R-r)=R^2 - r^2,.
Or, π(R^2 - r^2)/2 = π(12×12)/2= 72π.
Pink area = π(R^2 - r^2)/2 = 72π.
 Let the radius of the bigger semicirce be R and the radius of the smaller semicircle be r.
It can be observed that R^2=12x12-r^2. => R^2=144-r^2.
So, pink area=(1/2)
pi
(R^2-r^2)=(1/2)
pi
144=72*pi.
Let the radius of the bigger semicirce be R and the radius of the smaller semicircle be r.
It can be observed that R^2=12x12-r^2. => R^2=144-r^2.
So, pink area=(1/2)
pi
(R^2-r^2)=(1/2)
pi
144=72*pi.
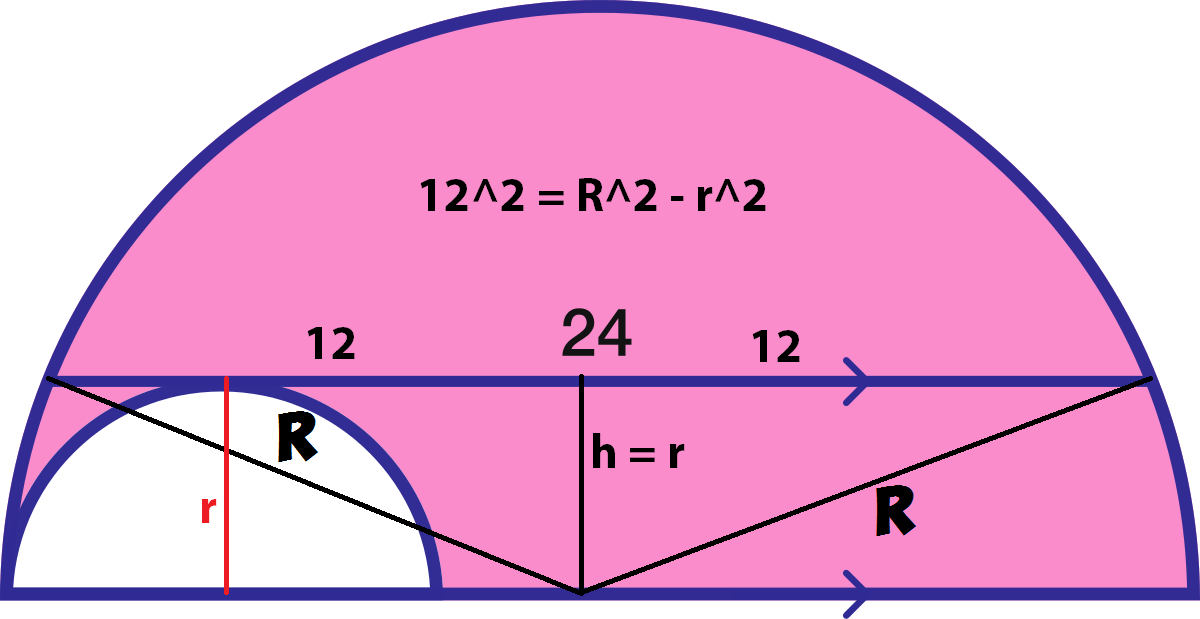
Area of Pink Region = 2 A - 2 a
= 2 π ( R 2 ) − π ( r 2 )
= 2 π ( R 2 − r 2 )
= 2 π ( 1 2 2 ) [Look in the fig, for this step]
= 72 π
LaTeX: L e t A C , the area of the large semi-circle A c , the area of the little semi-circle and A p the pink area
LaTex: As you can see, R = 3 r , A C = 2 π R 2 and A c = 2 π r 2
LaTeX: The area we are looking for is : A C − A c = A p ⟺ A p = 2 π R 2 − 2 π r 2
LaTeX: A p = 2 π R 2 − 2 π r 2 ⟺ A p = 2 π ( 3 r ) 2 − 2 π r 2 ⟺ A p = 2 8 π r 2 ⟺ A p = 4 π r 2
LaTex: As we have a cord [EF], we need half that cord : [ E F ] = 2 4 ⟺ 2 [ E F ] = 1 2
LaTex: the radii r and R and we get a right angled triangle. Applying the pithagorean theorem,
LaTex: we find the values of those 2 radii.
LaTeX: then we get : r 2 + 1 2 2 = R 2 ⟺ r 2 + 1 2 2 = ( 3 r ) 2 ⟺ r 2 + 1 2 2 = 9 r 2 ⟺ r 2 = 2 × 4 3 2 × 4 2
LaTex: Finally, the radii are : r 2 = 3 2 × 2 ⟺ ( r = 3 2 ) and ( R = 9 2 )
LaTex: The pink area is : A p = 4 π r 2 = 4 π ( 3 2 ) 2 = 4 π × 9 × 2 = 7 2 π
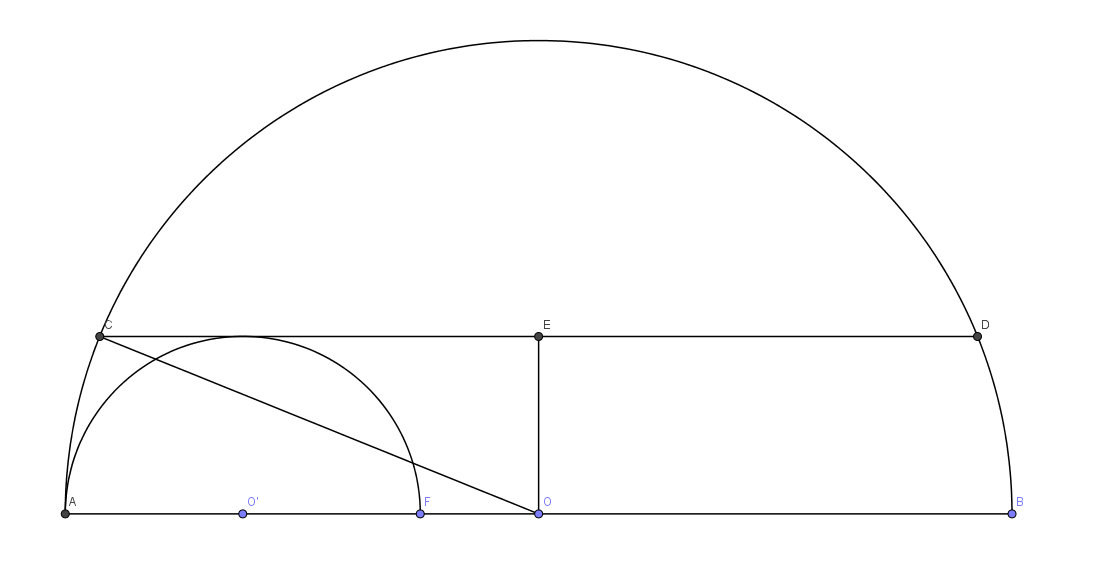
OC is the radius of the larger semicircle; so OC=R
We can apply the Pythagorean theorem in triangle OCE; O C = ( O E ) 2 + ( C E ) 2
OE=r
CE=12 (half of CD)
O C = r 2 + 1 4 4
So, r 2 + 1 4 4 = R
R 2 = r 2 + 1 4 4
The pink area is the difference between the areas of the semicircles: A = 2 1 π R 2 − 2 1 π r 2 = 2 1 π ( r 2 + 1 4 4 ) − 2 1 π r 2 = 7 2 π
Let the radiuses of big and small hemi-circles be r and r’. Forming a right tringle by connecting the center of the big hemi-circle to the right side of 24 unit chord and drawing a perpendicular from the center of big hemi-circle to this chord we have a right triangle and so 144 + r’2 = r2, or r2 – r’2 = 144. The area A of the pink part is: A = pi/2(r2 - r’2) = pi/2(r2 – r’2) = pi/2(144) = 72pi.
Let's call the radius of the small circle r and the radius of the large circle R. r is also the distance between the diameter and the chord, so you can draw a right triangle from the center to the edge along the chord (side lengths are 12, r and R). By Pythagorean Theorem, R^2=144+r^2. The pink area is (R^2-r^2) pi/2, which is 144 pi/2 or 72*pi.
We're given no information about the smaller diameter. Turns out, the pink area is constant for all such circles. That is, as the white area grows, so must the pink area in order to accommodate the chord constraint.
So, solve for the case when the diameter of the small circle approaches zero. The diameter of the large circle approaches 24. And the area of a half circle of diameter 24 is 72 π.
By Pythagoras theorem, R^2=r^2+(24/2)^2. Therefore, R^2-r^2=144. Finally, pinkArea=0.5 pi (R^2-r^2)=72*pi.
Don't these solutions all depend on an unstated assumption that the chord is parallel to the shared diameter? If the everything stated in the problem is true, but the chord tangent to the white circle isn't parallel to the shared diameter, none of the solutions shown seem to work!
Log in to reply
The chord is tangent to the semi-circle , so everything else follows
Made some changes to satisfy aesthetic norms !! ( Of course, aesthetics in mathematics is a far more complex affair !! :-) )
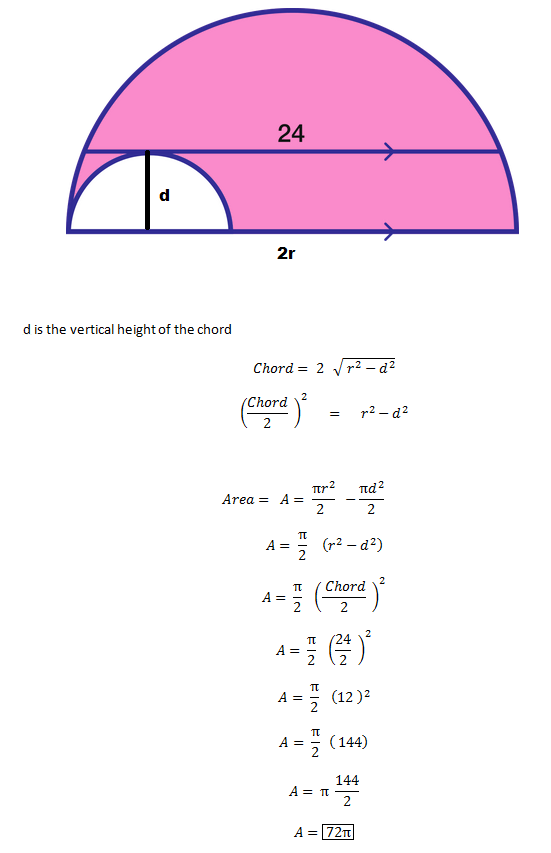

If the radii of the circles are r and R , then the cord is r above the shared diameter
Pythagorean theorem in triangle A B C gives us R 2 = r 2 + 1 2 2 or R 2 − r 2 = 1 4 4
Pink area = 2 π R 2 − 2 π r 2 = 2 π ( R 2 − r 2 ) = 2 π × 1 4 4 = 7 2 π
The beauty of the problem lies in the fact that the pink area does not depend on R directly. For example, the following pink areas are all the same size.