48 of 100: Knights, Knaves, and Werewolves
On a particular island, there live knights, who can only tell the truth, knaves, who can only lie, and werewolves, who can also only lie.
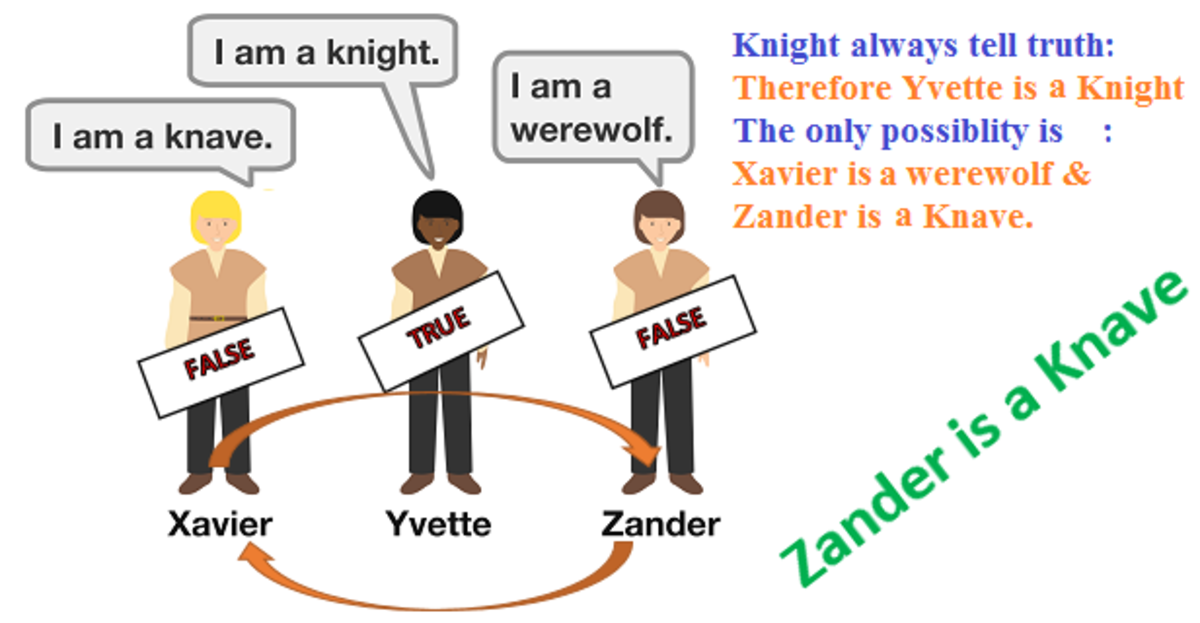
You come across a particular trio of native islanders named Xavier, Yvette, and Zander. They each make a statement:
If you know that amongst these three there is one werewolf , one knave , and one knight , then what must be true about Zander?
List all the possible cases if you're having trouble.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
29 solutions
Yes, the fact that Zander can be solved alone makes Xavier and Yvette superfluous, and this problem not as elegant as it could be
@Oliver MacLean Your reasoning for Possibility 1 is misleading. As a knight, Zander could have said any true statement, and not only "I am a knight."; e.g. also "I am not a knave.". The point, however, is that he could not have stated "I am a werewolf."
Since all of them are only speaking about themselves, the knight among them will always speak the truth, i.e. the knight will reveal it's identity, which in this case, is Yvette.
The remaining two always lie, so
⇒ Xavier is not a knave and Zander is not a werewolf.
⇒ Xavier is a werewolf and Zander is a knave. (As given in the question, that there is one knight, one knave and one werewolf amongst these three)
The real question, based on much recent experience with these truth teller problems at this site, is how this one rates more than one cactus.
Log in to reply
Probably yes, some questions in the entire 100 day challenge seem to be overrated.
wow u r so smart...
Yvette isn't necessarily a knight, as she may be a knave or a werewolf lying. I think it's impossible to determine a stated knight's identity, but I might be wrong.
Log in to reply
If more than one person had claimed to be a knight, that would be an issue. But even if Xavier had claimed to be a knight in addition to Yvette, I think you'd still be able to tell that Zander was the knave.
Please read my first statement, and the cases you're explaining are applicable only when you consider a single person, else if you consider the complete situation, your cases are inconsistent
Log in to reply
Sorry, I misread some parts, I was referring to the statement of "in this case is Yvette" but I did not read the question/comment fully. My apologies.
The only person that can say: "I am a knave" is a werewolf "I am a werewolf" is a knave
Anyone can say "I am a knight"
But a knight must say "I am a knight"
Since Zander says "I am a werewolf", he must be a knave.
Yvette is a knight. Since knights tell the truth, the only knight present has to say she is a knight. And no one else is claiming to be a knight.
The others both lie, since there are no more knights left in the group.
Zander says I am werewolf. So Zander is a knave, the only other option being taken.
Xavier can be neither a knight nor a knave - so he is the werewolf. Which implies Zander is lying - so Zander is the knave!
If Zander was a knight he would tell the truth and say that he was a knight, if he was a werewolf then he would lie and say he was't a werewolf so he must be a knave who is lying about being a werewolf.
| Knight | Knave | Werewolf | |
| Statement | Truth | Lie | Truth or Lie |
| Yvette "I am a knight" | True | False (She doesn't lie) | False (She doesn't lie) |
| Xavier "I am a knave" | False (He lies, he cannot be a knight) | False (He lies) | True (The only choice left) |
| Zander "I am a werewolf" | False | True (The only choice left) | False |
LaTeX: Zander is a knave.
1.Yvette says- he is a knight.as knight never tell lie and without him nobody is claiming him as a knight ,so Yvette must be true.
secondly, knave never tell true ,they always lie. so, a knave will never concede himself as a knave in front of people as people hate knaves.
again, werewolves also can only lie.
so, the knave and werewolf both lied and hided their identity. so, the knave is actually a werewolf and the werewolf is actually a knave as there are only 2 options for them. .
thirdly, so the werewolf or Zander will be the knave
If either of Xavier or Zander were knights, then they would be lying. Therefore, Yvette must be a knight.
Hence Xavier and Zander are both lying (it is given that there is are 2 liars and 1 truth teller).
Zander says he is a werewolf but we know he is lying, so therefore he must be a knave.
how u know is he does not even look like a wearwolf
You can find out what Zander is just by his own statement. If he is a knight, he would say he is a knight, so under is either a knave or a werewolf. If Zander is a werewolf he would say he is either a knave or knight, so he can't be a werewolf. That only leaves out one possibility: knave, and if he is a knave, then he would lie, and he did because he said he was a werewolf. So Zander is a knave.
First, anyone saying "I'm a Knave" or "I'm a Werewolf" can't be a knight.
That means Zander is either a Knave, or a Werewolf.
That also leaves Yvette with the only person possible of being a Knight.
Next, since we found the face that Xavier and Zander always lie, that means Zander is a Knave and Xavier is a Werewolf
First let's look at Zander.
Fact 1: Zander says he is a werewolf.
Fact 2: If Zander says he is a werewolf, then he can't be a knight because a knight would truthfully say that he/she is a knight.
Fact 3: Since, Zander says he is a werewolf, he can't be one because a werewolf would lie and say that it was either a knave or a knight.
Fact 4: Zander then must be a knave.
The knights can't lie, so they can't say they're a knave or werewolf. So, we know that Yvette is a knight. Werewolfs and knaves can only lie, and there are one of each,so Zander is a knave and Xavier a werewolf
did i do good?
only knaves can say i am a werewolf since knights are not werewolves so they cannot lie and werewolves could not say that since they always lie
@alex wang , i feel connected to u. I am also very young and have joined brilliant when i was 7!!!! I also LOVE LOGIC and LOVE HARRY POTTER (sorry i just had to write that)
Zander can only be a knave since if he is a knight, he lies, therefore is a knave. If he is a werewolf, he says he is a knave, so he is a knave. Therefore he is a knave.
A knight can only tell the truth.
A knave has to lie and so, can claim that s/he is either a knight or a werewolf.
A werewolf also has to lie and can claim that s/he is a knight or a knave.
But a knight is forced to tell the truth and can only say, " I am a knight".
According to the question, there is only one knight in the group. And there is only one person claiming to be a knight - Yvette. So, Yvette is the knight.
Zander is either a werewolf or a knave (since the question says that the group has a knight, a werewolf and a knave).
In both cases, he is lying, since both werewolves and knaves only lie.
So, since Zander claims that he is a werewolf, he is actually a knave.
Xavier and Zander must both be lying since they cannot say that they are a knave and a werewolf. Yvette, then, must be the knight. Since both Xavier and Zander are lying about their respective identities, Zander then must be a knave.
You can actually identify all three.
The only location that the Knight can occupy is 'Yvette' since a Knight uttering any of the other two phrases would be a lie. The only location that the Werewolf can occupy is 'Xavier' since the Knight's spot is taken and the Werewolf must lie The only location that the Knave can occupy is 'Zander' since the Knight's spot is taken and the Knave must lie.
@Abhiyansh Raj Pls send ur paper.You havent sent it till now.I asked for it yesterday too.My mail is [email protected]
I didn't have ur no thats why but i will send it soon to ur email
@Kaustubh Miglani did u receive it
@Abhiyansh Raj Yeah thanks I will solve it now
1-----Answer is 3 2------Answer is 5/00 I am not sure Rest I will tell tomorrow
Q-1>>>Answer is 3 Q-2>>>Answer is 5/00 Q-3--->>>Answer is 7
@Kaustubh Miglani pls post the solutions here if possible
Log in to reply
@Abhiyansh Raj Ask Kartik Malik,I have given him soln and explanation and answer of many question
Xavier and Zander are lying.
We know this because they are saying "I can only lie", which if a true statement, would be a paradox. Therefore we can conclude that they are liers.
Zander is lying about being a werewolf but he is not honest so we know he is a knave.
As there is one of each type, only one can be telling the truth (and two must be lying):
If the truthful one is Xavier or Zander, then their statement must be true, so they are what they say they are. However, what they say they are is a werewolf and a knave which both lie, which is contradictory.
Therefore, Yvette is telling the truth, and she is the knight. This leaves Xavier and Zander as the werewolf and the knave. As both of their statements must be false, they are the opposite of what they say, meaning that Xavier is a werewolf and Zander is a knave
A Knave cant say "I am a Knave" and Knight too. So Xavier must be Werewolf. A Knight can only say, he is a Knight. Therefore Zander is a Knave.
As the knight always tells the truth, he must admit his identity. So: Yvette is the knight.
As both werewolf and knaves are liars and Zander is one of them, he must be lying. Hence, he is not a werewolf. He is a knave.
A Knight tells true and we have only 1 knight in the island. So, Yvette is the Knight. As he speaks truth, so rest two tells lies. Zander tells lie and he is not a knight already. So he is also not werewolf. Only option left is Knave, so he is a knave.
Xavier
definitely lied because neither a knave nor a knight can make such a statement therefore he is a
werewolf
.
According to the fact that Xavier is a
werewolf
,
Zander
has lied and he is a
knave
.
Zander says, "I am a werewolf." If the statement is true, then as a werewolf he must lie, then he is not a werewolf, which contradict with our assumption that the statement is true. Therefore, the statement is false and Zander lies and he is not a werewolf. Since he lies and not a werewolf, he must be a knave .
- Xavier is a werewore who lies that he is a knave.
- Yvette is a knight who tells the truth.
- Zander is a knave who lies that he is a werewolf,
You can figure out this problem by trying to figure out what Xavier is first. Xavier has to be a werewolf. Why? Because he says that he is a knave. He is lying, because if he told the truth he would be a knight, but if he were a knight, then "I am a knave" would be a lie. Point being that he is lying. But, because of the fact he is lying, he has to be a werewolf. A knave would lie and say something else. That means that Zander is a knave or a knight. He says that he is a werewolf, but Xavier is one. That means that he is lying. So, the only other kind that lies is knaves. That means that Zander must me a knave.
The problem can be solved by only considering Zander.
Possibility 1: Zander is a knight. If this were true, then Zander could not say that he is a werewolf*, so there is a contradiction.
Possibility 2: Zander is a werewolf. If this were true, he could not say he is a werewolf.
That leaves possibility 3: Zander is a knave. This is consistent because saying that he is a werewolf is a lie.
* - edited to correct for point made by Tom Verhoeff