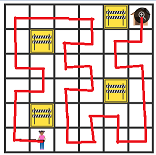
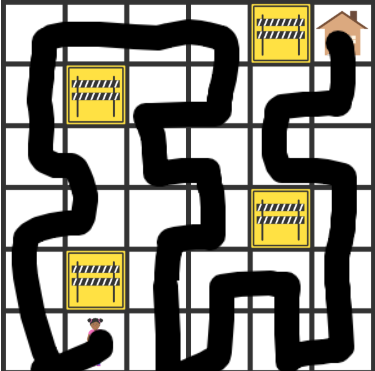
49 of 100: Mathematical Meandering
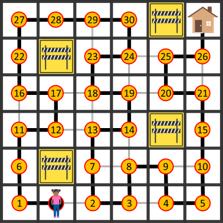
Zara is finding her way home, but she wants to take a route that visits her neighborhood as much as possible. From any square on the map shown, she can move up, down, left, or right a square (not diagonally).
She also wants to visit every empty square exactly once , entirely avoid the squares marked with "under construction" signs, and she wants her trip to end at her house.
Is it possible for her to do this?
You can just start drawing paths, or you can use logic!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Great logical deduction!
Beautifully clear explanation! This is how I solved it. It is amazing to see how the apparently many path options quickly narrow to one.
Missed this one, but happy to learn your method :)
That is beautiful
A clear, precise solution is always best!
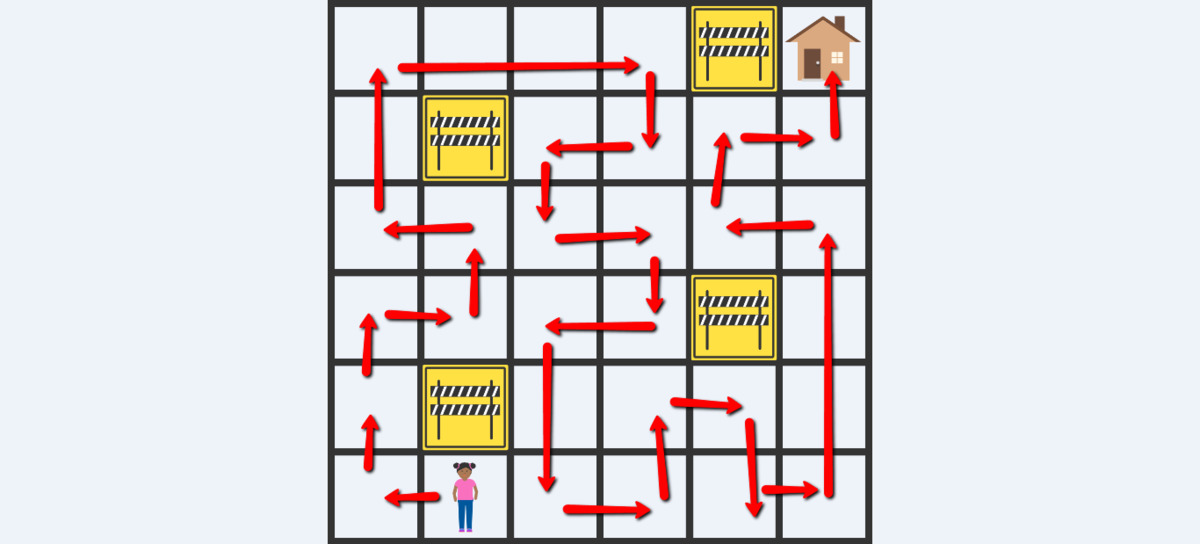
It's not hard to show this is the only path. We only need that the path is fixed at every corner.
This was a Hamiltonian paths problem. I tried to find all such paths, and determined that there was only one such way of doing so. I created a script that found all Hamiltonian paths between two points on a graph, as can be demonstrated below.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
I used a chessboard labelling to identify each square (letters at the bottom, numbers on the side). This outputs
1 2 |
|
Its really confusing
I for one appreciate the programming approaches, as there are usually many ways to approach the problem. Sharky's solution uses a Python Pattern associated with Graph Theory. Recognizing patterns is a key to becoming a good problem solver, whether or not code is used. And thanks to this, I have a new technique in the tool box.
With this algorithm, it would now be very easy to find out which squares Zara could start from that do not have a solution.
What would be cool is to generalize the program by building of the connections1 dictionary from the board configuration and the list of forbidden squares.
Really cool would be to incorporate Mark Dawes recursive two-way square partial paths algorithm to help solve really big problems.
Using a computer to do brute force, is still brute force.
Log in to reply
I never claimed it wasn't brute force. I saw the path easily, but I wanted to determine all such paths. Using a computer made this much easier.
I don't think Sharky claimed otherwise
It is quite fun to see that there is only one solution. There is only one way of getting into and out of a corner square. This applies to either a true corner square or a pattern of squares that is essentially a corner created either by blocked squares or squares already visited.
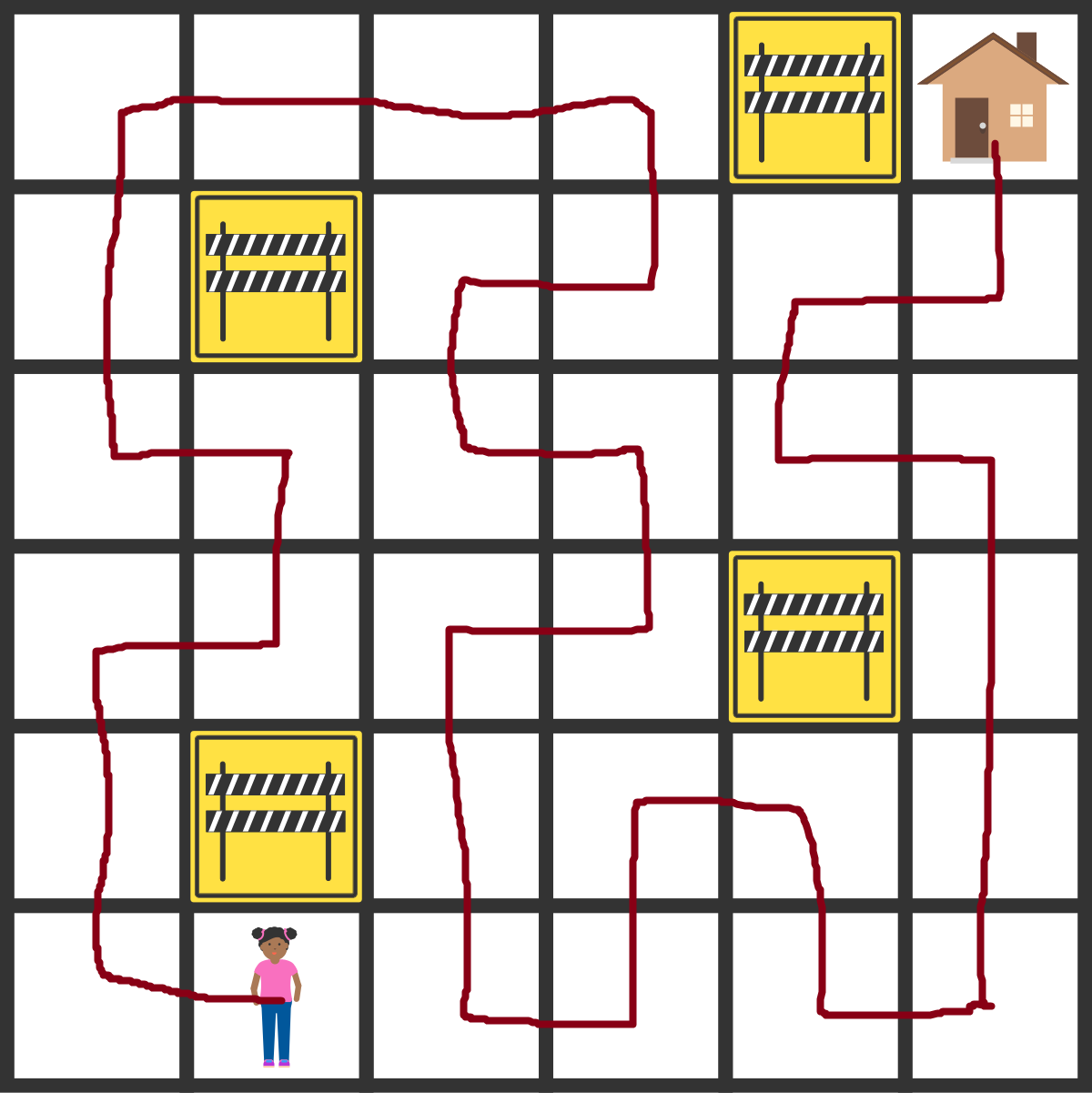
We start as in the left picture, showing how the path must go through the obvious corners. We then proceed to make forced joins between path sections, and fill in newly created corner turns. Doing this successively as shown, we end up with the RH diagram as the only solution.
But I don't know if this is the only possible path.
I found it easy if one started at the house and worked backward to Zara. Edwin Gray
I used a constructive graph-theoretic approach. Sharing it for those interested. It looks equivalent to
@Mark Dawes
' solution. (Well done, Mark.) Start by creating a graph
G
from the problem.
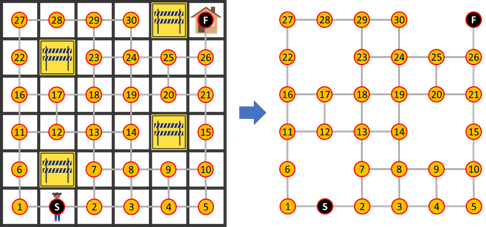
Problem:
In graph
G
, construct an S
→
F path
P
that visits every node (at most once, by definition of a
path
).
Fact:
each node in
P
except S and F is required to have degree 2 (i.e., be between exactly 2 path edges), while deg(S) = 1 = deg(F) in
P
.
Iterate by alternately adding or eliminating possible path edges from G as follows:
(A) Add non-path edges from G to P if those edges are the only way to satisfy a node’s degree requirement in P .
(E) Eliminate all non-path edges from G at each node if the node’s degree requirement in P has been satisfied.
STOP if either all node degree requirements are met (path found) or no more non-path edges can be added or eliminated (no path possible).
Algorithm iterates are shown below where edges in red are added or eliminated based on the degree requirements of red nodes.
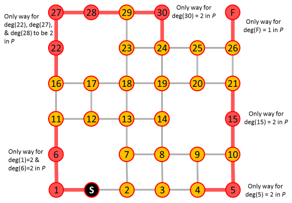
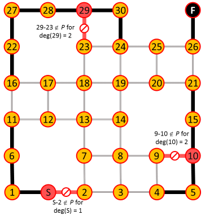
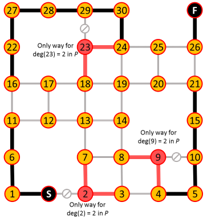
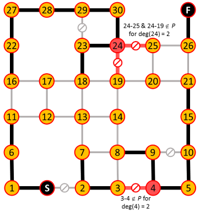
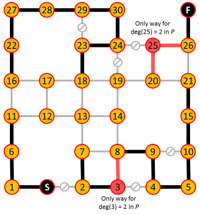
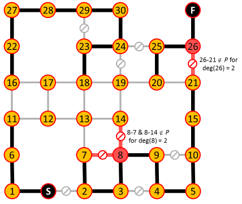
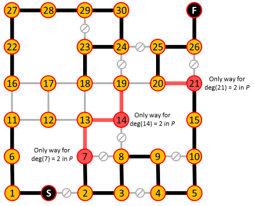
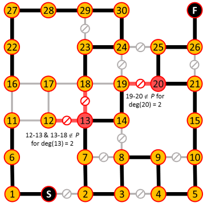
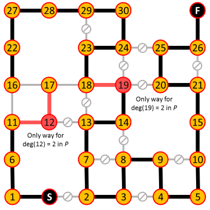
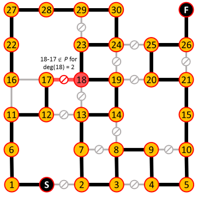
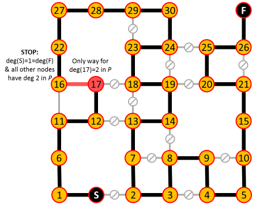
This construction also shows the path is unique.
This is very clear - I like it a lot. It's also a more formal way to do it. Thanks for taking the time to create the diagrams (which is a time-consuming job!).
she could because she could go left up and left.(
I don't know if this is valid reasoning, but this is what I did.
I overlaid a checkerboard pattern on top of the grid. Whenever Zara moves from one square to another, the color of the square must change. Of the squares that are "under construction", there is a pair that is one color and a pair that is the other color. This means that there is an equal number of squares of each color remaining, and there is a valid path.
Imagine the grid as a chess board with the home being black. Then Zara is starting on a white space. This means she must take an odd number of steps to finish on a black space. There are 36 spaces on the board, meaning 35 steps to cover the entire board. Taking the construction into consideration, we subtract 4 from 35 to give Zara 31 steps, meaning she will end on a black space hence making it possible.
You have found a necessary condition for such a path to exist. Unfortunately, it need not be sufficient. Do you see why?
Log in to reply
Oh I guess if the construction completely blocked off the home this would still say you could even thought it would be impossible.
Log in to reply
Good observation. Are there other scenarios where we remove 2 black and 2 white squares such that home isn't completely blocked off (meaning that there is always a path from home to any unremoved square), but such a path visiting every empty square exactly once doesn't exist?
Log in to reply
@Calvin Lin – Yup cases where construction would force Zara to visit the starting square again. Didn't realize any of this at the moment haha.
Log in to reply
@Roy Han – Indeed! For example, if the starting square was ( 1 , 1 ) , and the square ( 2 , 2 ) was blocked, then there isn't a way to visit both of ( 1 , 2 ) and ( 2 , 1 ) .
Learn something new every day :)
But this does do the job of telling you that it is worth trying at least. Had you had 5 construction spaces, it would have proven there is no point in trying.
Think it opposite, ie from home to its initial position

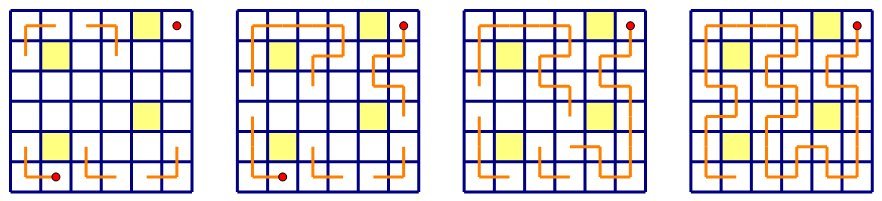
One way to start is to focus on the squares that only have two ways they can be accessed. These are shown with a star: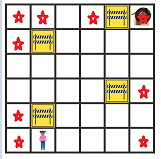
Now let's draw in the part of the route that these imply. If it's going to be possible to make a full route then it must include these.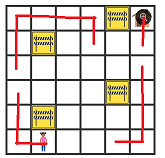
Now there are some new squares that only have two access points. They are shown with a star: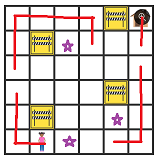
Put the route-fragments in for these too.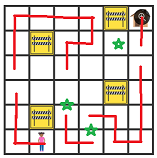
Repeat the process ...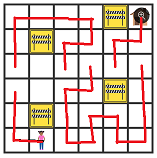
... until finished: