54 of 100: Circle of Truth and Lies
On a certain island there live only knights, who always tell the truth, and knaves, who always lie.
One day you find 10 island natives standing in a circle. Each one states: "Both people next to me are knaves!"
Of the 10 in the circle, what is the minimum possible number of knights?
Remember you don't want just any configuration, but one that has the minimum number of knights.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Upper bound
With a similar idea and knowing that there can't be two knights next to each other, we can show that N ≤ 2 n , with n the number of people. Therefore, the number of knights must be between ⌈ 3 n ⌉ and ⌊ 2 n ⌋ .Bounds are minimum and maximum
For all number n of people, it's easy to see by induction that we can always find configurations with these bounds:
- Cases n = 3 , 4 , 5 can be verified as they have only one configuration each: A A I , A I A I , A A I A I .
- For any n ≥ 6 , a minimal configuration can be obtain from a minimal configuration of n − 3 , changing a I in I A A I .
- For any n ≥ 5 , a maximal configuration can be obtain from a maximal configuration of n − 2 , changing a I in I A I .
| Number of people | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ⋯ | n | ⋯ | |
| Min knights | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | ⋯ | ⌈ 3 n ⌉ | ⋯ | |
| Max knights | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | ⋯ | ⌊ 2 n ⌋ | ⋯ |
Each knight must be bordered by two knaves, and each knave must be next to at least one knight. A knave may be next to 2 knights, but that is redundant so as many knaves as possible should be bordered by a knight.
This means that you should have as many groups as possible of a knight bordered on both sides by a knave. Since that is 3 people per group, you have three groups consisting of knave-knight-knave. Add in the last person, who is bordered on both sides by a knave and, therefore, must be a knight, and you have an optimal solution:
knight - knave - knight - knave - knave - knight - knave - knave - knight - knave
This is the fewest number of knights you can get, because you can't replace any of the existing knights with knaves, nor is there a way to more efficiently utilize the current knights.
The conditions force: a) no knight is next to another knight b) no knave is next to two knaves. Every knave must be next to at least one knight. If there were only three knights, this would be impossible, as the seven knaves would be in at most three groups of consecutive knaves, one of which have to have at least three knaves. With four knights, it is simple enough to ensure we don't get three knaves in a row or two knights in a row. Letting G=Knight and V=Knave, one possibility would be
G - V - V - G
V (middle) V
G - V - V - G
Each Knight must have two Knaves near him, a Knave can have two Knights or a Knight and a Knave near him. Beginning with a Knight at 12 o'clock we can put two Knaves and a Knight, and a Knight between the last three position.
With this pattern the minimum number of Knights is 4

Our Aim is to find minimum Knight or Maximum Knave.
1. If everyone is knave, the statement of everybody would be true. So 0 knights are impossible.
2. Start with a Knight, who is truthful. Fill up two knaves beside him.
3. You can put the next person either as a knave or a night. But if we do so we would have 2 knaves at side of each knight and total no of knights would be 5.
4. Our aim is to minimize knights, so we put knights at 1,4,7 th position.
5. Next one should be 10th one, but as the 10th one is already a knave as stated by 1st knight, we put a knight at 9th.
6. So, total no of knights= 4 in minimum. !
there are 4 knights, OK .but they wanted the minimum value. why their can not be less than 4?
Log in to reply
No. Because you have to have 1 knight at every 3 positions. So at least you need 4 knights. If you don't have a knight in every 3 place, there would be 3 consecutive knaves. This will make the middle knaves statement true who should not tell truth.
i think this is not a tough problem to think.
as,Each knight must be bordered by two knaves, and each knave must be next to at least one knight. A knave may be next to 2 knights,
so, at first---knave always tell lie. that mean they want to do harm to others.so, if they are bordered by knights they will tell lie.again if one of them beside is knave they will also tell the same.
secondly------------No three knaves can be next to each other; otherwise, the middle one would fail to lie.
so, every 1 out of 3 must be a knight.that means their must be more than 3 knights .that means minimum possible value of knight is 4
their can be another guess---all of them are knaves. but that is not expected.
If a knave (-) says 'both people next to me are knaves', it cannot be true, so at most two knaves in row may occur.
If a knight (+) says it, it must be true so two knights in row cannot occur.
So possible pattern minimizing the number of knights is - - + - - + ..., but we have to be a bit careful how to close the circle, - - + - - + - + - + is an example. Less is impossible, because having 3 knights would mean having 7 knaves. The knights would divide them up in 3 groups, so that at least one group would be of size 3 or more.
The key is thinking knave lie implicates 2 options:
1) Both people are knights. OR 2) ONE IS A KNAVE AND THE OTHER IS A KNIGHT.
Pretend the person at the top is a knight that means the people next to him must be knaves which also means the people next to them must be knights and so on.
That, of itself leads to 5 knights. The question asked for the least number possible. It is possible to have 'knight, knave, knave, knight and fulfil the criteria, thereby hiving only 4 knights.
I order to satisfy the constraints of the problem
-
each knight must be surrounded by knaves
-
each knave must be next to at least one knight
As a result (using A for knight and B for knave) the following patterns are possible
BABABA..., BABBABBA... or some combination of both such as BABBABA...
From these two patterns the least possible number of knights would occur when knaves are doubled between knights. The problem with this is that 10 does not divide evenly by three so then we know that a combination pattern is required for example (where A' is the first knight)
A'BBABBABABA', A'BABBABBABA', A'BABABBABBA', A'BBABABBABA', A'BBABABABBA', ...
It turns out any pattern of two ABB, and 2 AB will work.
There's at least one knight or they'd all be telling the truth, so start with that knight and work your way round the circle. The 2nd and 10th are knaves because the known knight's statement, and the 3rd and 9th can be either but let's maximise knaves to minimise knights. 4th is a knight, so is the 8th. We can't have 3 consecutive knaves so let's pick the 6th to be our last knight for a total of 4.
A matter of combinatorics. If one has 3 A's and 7 B's there is no arrangement of the 10 letters without 3 B's in a row. With three knights and seven knaves there would be three knaves in a row when the middle knave would be telling the truth. Consequently, there must be at least four knights each surrounded by knaves e.g. A-B-A- A-B-A- A-B-A- B-.
We know that there cannot be three knaves in a row since the middle knave in that sequence would be telling the truth. When starting with a configuration of all knaves, we must separate the knaves with knights, so that the maximum number of consecutive knaves in between knights is two. If we keep that number equal to two for as long as possible, this sequence appears:
(knave - knave - knight - knave - knave - knight - knave - A - B - C )
A cannot be a knave because this forces B to be a knight, then C to be a knave. This results in three consecutive knaves.
Therefore A is a knight, B forcefully becomes a knave, and C forcefully becomes a knight.
The result is this configuration: (knave - knave - knight - knave - knave - knight - knave - knight - knave - knight)
Therefore the minimum possible number of knights is 4.
This shows that 4 is a possible answer, but is it optimal? Why is 3 impossible?
Log in to reply
If you follow the chain starting from the top-most figure and arbitrarily labeling him Knave, for him to be a knave , it is enough if either the person to the left or right is a knight. Here , we chose the person on our right (clock-wise) to be a knight. So, if we keep doing this around the circle, i.e ensuring that there is at least 1 knight bordering a knave,we come to the person to the left(viewer's left) of the person we started with. if we label this person a knave then we have a situation where there are 3 consecutive knaves which is self-contradictory since a knave cannot be between 2 other knaves. Hence, this person has to be a knight.
Log in to reply
In general, it seems that except for the final person, in a minimal knight configuration, for every 3 persons, there is 1 knight. So for n persons, there will be a minimum of ceiling(n/3) knights where ceiling(x) denotes the lowest integer higher than x. So for n = 10, there will be ceiling(10/3) = 4 knights.
Log in to reply
@Sundar R – That's good! Just wanted to make sure your solution proved your picture was optimal, for completeness sake.
This is not a proof it is only a picture.
Log in to reply
It depicts one configuration. The starting position was chosen arbitrarily. One could have started anywhere and ended up with similar results. So , one can generalize using principles of symmetry
Log in to reply
Exactly what I said, a picture not a proof. There is no supporting argument of any kind, just one configuration.
For a Knave's statement to be falsified, it is enough if one person on any of the sides is a knight. Further , this knight can border more than one knave in a minimal knight configuration
This is a way of doing it:
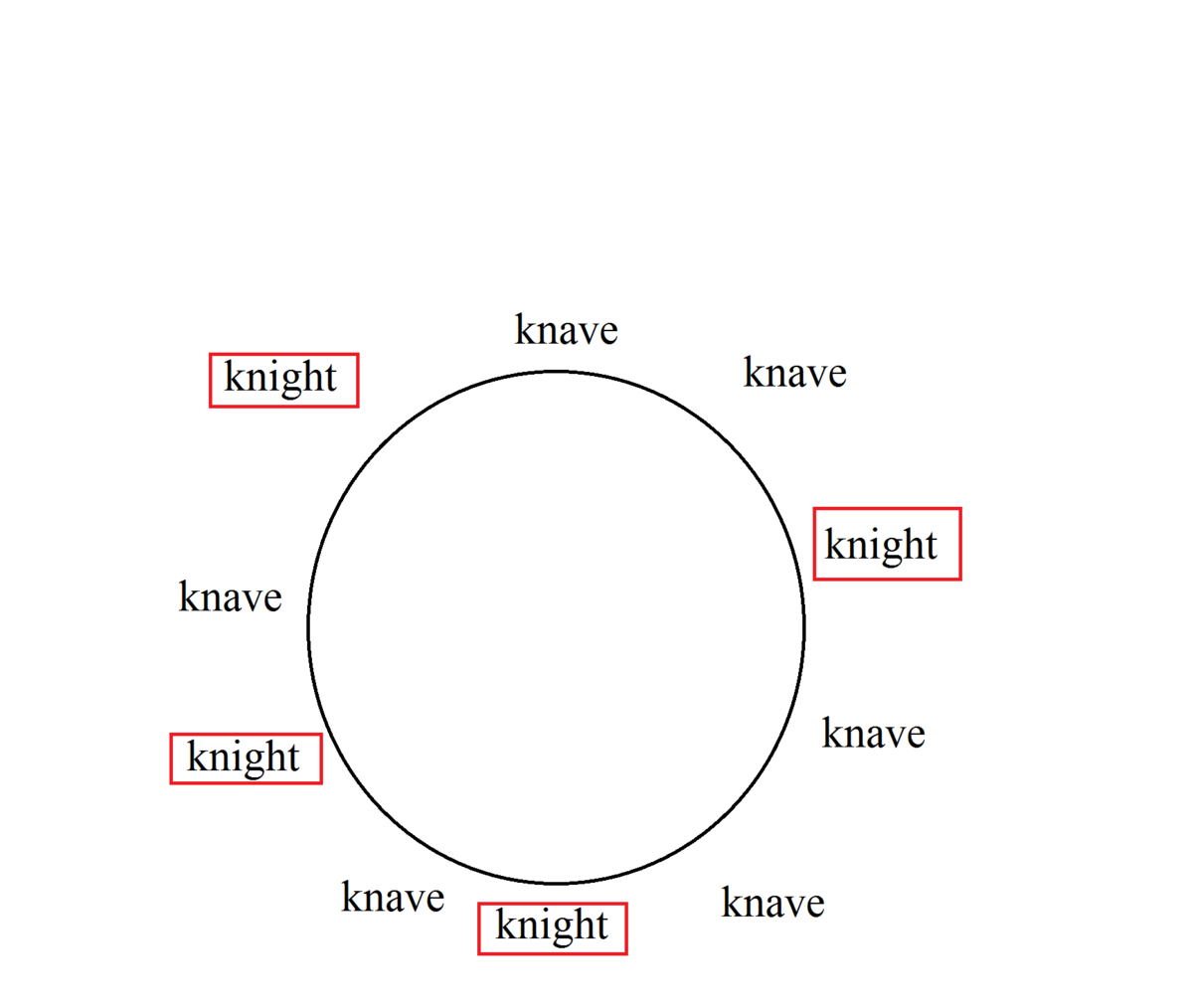 As shown above the minimum number of knights is
4
As shown above the minimum number of knights is
4
You've shown that it is possible to have an answer of 4, but is four the lowest? Why can't here be 3?

No three knaves can be next to each other; otherwise, the middle one would fail to lie.
Therefore at least one out of three must be a knight, making N ≥ 3 1 0 = 3 3 1 . Thus N ≥ 4 . It is not difficult to find a configuration with this number (e.g. A A I A A I A I A I ).