62 of 100: A Weighty Issue

Adding a triangle-square pair on the left plate adds three units of weight to the right. (fig1 & 2) From which it is possible to conclude that one such set weighs 3 units.

$$ $$

3 units of weight + a circle on the left plate equals 9 units on the right. (fig 1) So the circle weighs 6 units.

$$ $$

2 circles and a triangle-square pair would weigh: $2\times6 + 3 = 15$

Three more triangles + above balances 18 units of weight. (fig 3)

$$ $$

Therefore, three triangles weigh 3 units.

A single one weighs $\boxed{ 1 unit }$ .

$$ Basically its algebra in words. But the key was to pair each square with a triangle, which makes it easier to think in the head.

Subtract three times the first scale from the sum of second and third scales. This way squares and circles vanish. You left with three triangles and $3 \times \text{triangle} = 18+12-27=3 \ \ \ \ \Longrightarrow \ \ \ \ \text{triangle} =1$

Let C be weight of circle, T be weight of triangle, and S be weight of square.

From adding the last 2 scales, we have that

3C+3S+6T=30

So,

C+S+2T=10

Since we also have C+S+T=9

Therefore, by subtracting we have

$\boxed{T=1}$

Adding 2nd and 3rd scale makes it a multiple of the 1st scale (triple, to be specific) plus 3 triangles. Subtracting the triple of 1st scale from this sum straight away gives the weight of 3 triangles as 3, meaning thereby that the weight of one triangle is 1.

Let the respective measurements be equations $(1)$ , $(2)$ , and $(3)$ .

The difference between $(2)$ and $(1)$ is a square and a triangle, so we have

${\color{#3D99F6}{S}} + {\color{#20A900}{T}} = 3$

Now add $(1)$ to $(2)$ so that

\begin{aligned} {\color{#69047E}{CC}} \ {\color{#20A900}{TTT}} \ {\color{#3D99F6}{SSS}} & = 21 \tag{1 + 2} \\ {\color{#69047E}{CC}} \ {\color{#20A900}{TTTT}} \ {\color{#3D99F6}{S}} & = 18 \tag{3} \end{aligned}

Subtracting $(3)$ from $(1 + 2)$ , we have

${\color{#3D99F6}{2S}} - {\color{#20A900}{T}} = 3$

Finally, setting that equal to our first equation, we have

$\begin{aligned} {\color{#3D99F6}{S}} + {\color{#20A900}{T}} & = {\color{#3D99F6}{2S}} - {\color{#20A900}{T}} \\ {\color{#3D99F6}{S}} & = {\color{#20A900}{2T}} \\ \implies {\color{#20A900}{T}} & = \boxed{1} \end{aligned}$

The triangle $=1$

My method using algebra:

The Circle = C The Triangle = T The Square = S

1. C + T + S = 9

2. C + 2T + 2S = 12

3. 2C + 4T + S = 18

Using simultaneous equations we can find out what C is.

(C + 2T + 2S = 12) - (C + T + S = 9) = T + S = 3

If 'T + S = 3' then 'C = 9 - 3 = 6'

2C + 4T + S = 18

Substitute C for 6:

2(6) + 4T + S = 18

12 + 4T + S = 18

4T + S = 18 - 12

4T + S = 6

Since 'T + S = 3' then T and S must be (1 and 2) or (2 and 1)

4(1) + S = 6

S = 6 - 4

S = 2

T = 1

Nice, it really can be solved just in your head.

Note that if you subtract 9 from 12 you will find weight of SQUARE plus TRIANGLE

After you subtract 3 from 9 you will find weight of CIRCLE

After you subtract 6 and 9 from 18 you will find weight of THREE TRIANGLES

First, let's ignore the 3rd one and think one triangle and one square as one pair.

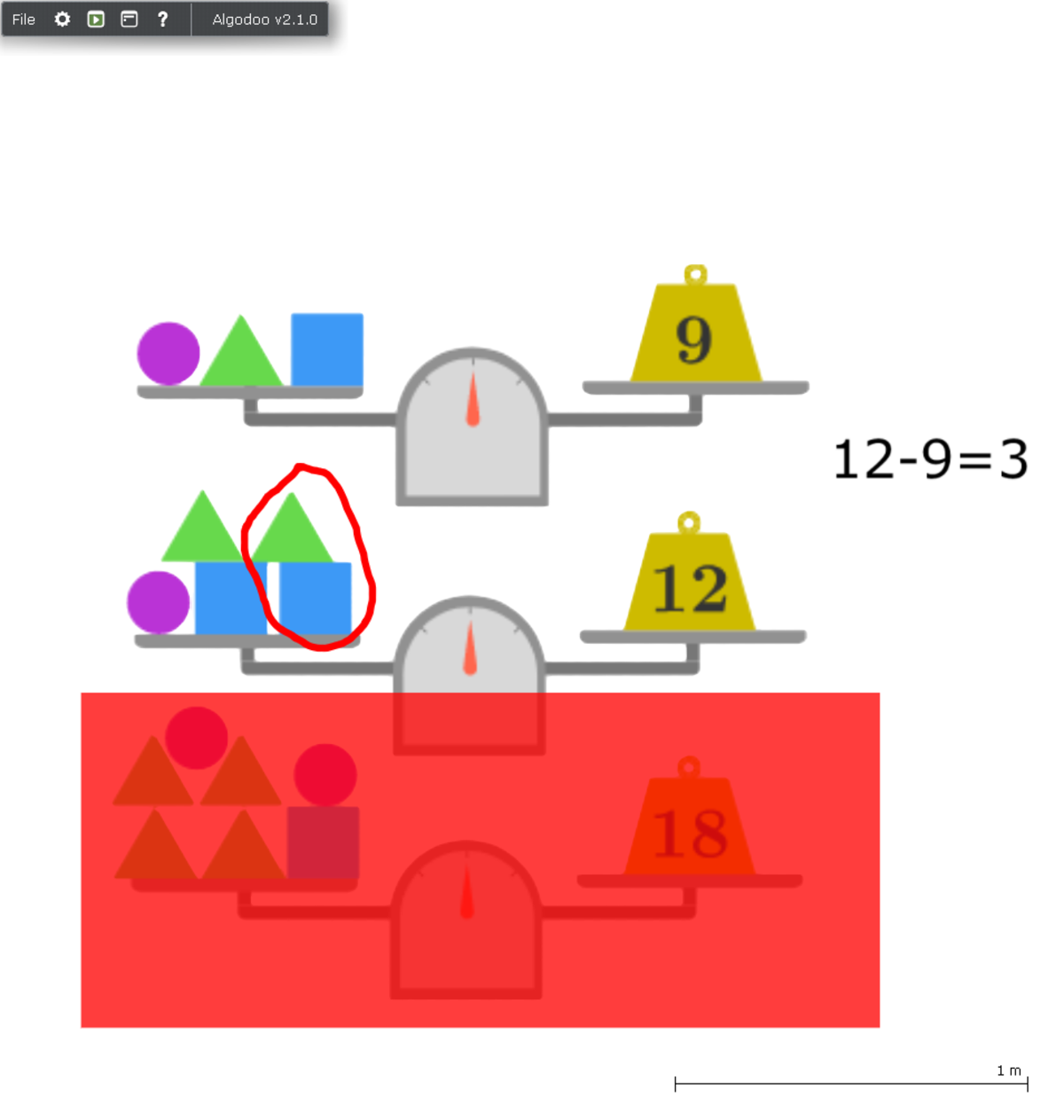
So we know that one pair equal 3 and also we know thet one Circle equal 6.

Next, Let's look at the 3rd one.

We already know that one circle equal 6, so we can subtract 6x2=12 from 18.

There also is one pair so let's also subtract 3 from 18-12=6

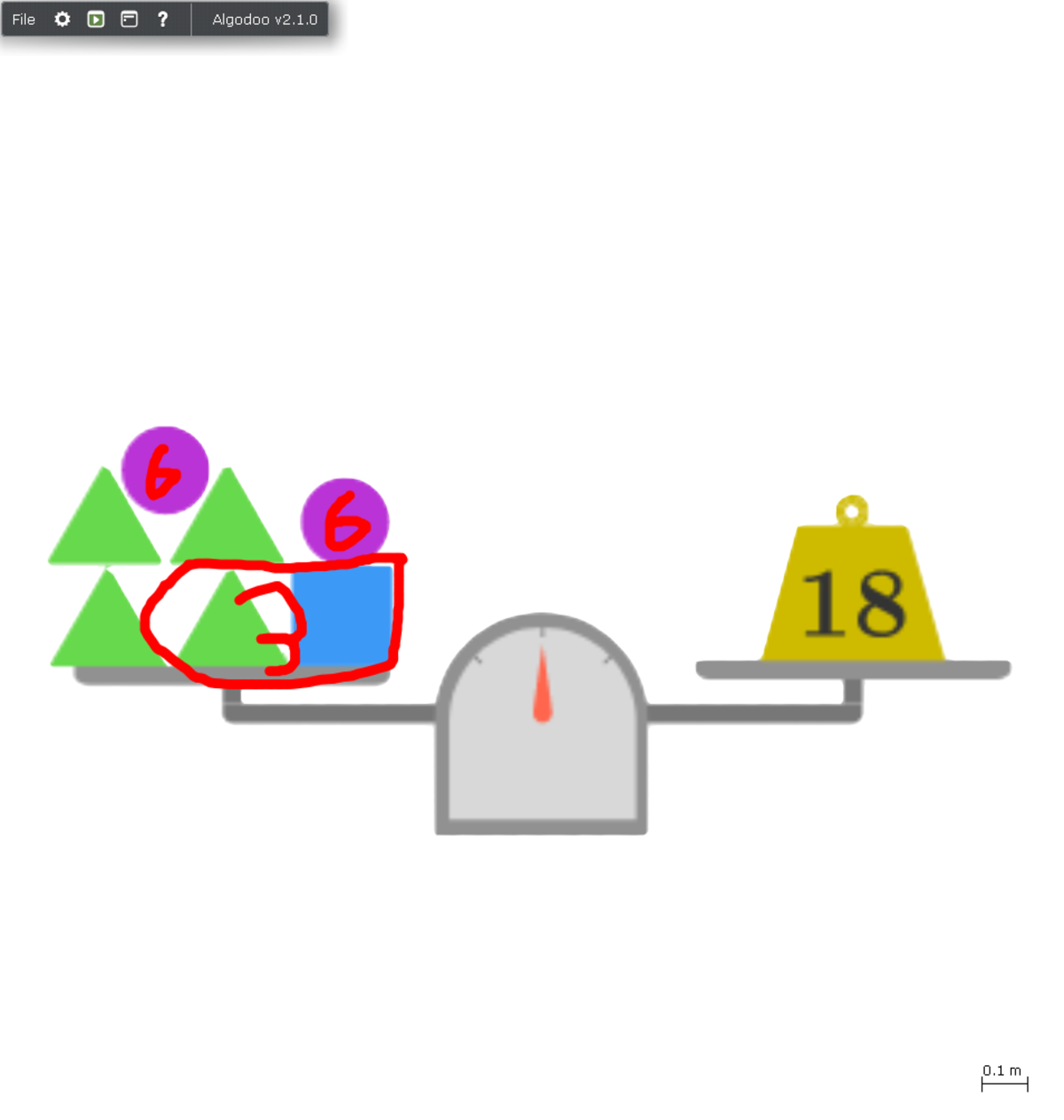
So 3 divided by 3 is 1.

Hence, one triangle equal 1.

The weight of one of each combined is 9 and the weight of 2 triangles, 2 squares and 1 circle is 12. Since the second scale is 1 circle away from double the first and only has a difference of one circle, 9 doubled minus 12 would give us the value of one circle which happens to be 6. So then we take away the circle from the first scale and are left with 3, resulting in 2 possibilities, 1) TRIANGLE = 2 and SQUARE = 1 or 2) TRIANGLE = 1 and SQUARE = 2. We take away the 2 circles from the third balance resulting in the remaining net weight to be 6. From here, it is a matter of trial and error. 1) 4T * 2 + 1S * 1 = 9 which is incorrect so it must be 2) 4T * 1 + 1S * 2 = 6.

T = Triangle S = Square

Maak het verschil tussen bovenste en de middelste balans. Reultaat is 3 en is gelijk aan de som van 1 driehoek en 1 vierkant. Dus is 1driehoek 1 of 2 en een bol is 6. Pas deze waarden toe in onderste balans met 'driehoek' = 2 en de balans is niet inevenwicht. Dus moet een driehoek 1 zijn.

Double the first scales (2 circles, 2 triangles, 2 square = 9 x 2 = 18)

Compare to the second scales (1 circle, 2 triangles, 2 squares = 12)

So, one circle = 6

================

Double the second scales (2 circle, 4 triangles, 4 squares = 12 x 2 = 24)

Compare to the third scales (2 circles, 4 triangles, 1 square = 18)

So, 3 x squares = 6; so, one square = 2

================

Looking at the first scales, triangle, circle, square = 9; so triangle = 9 - 6 - 2 = 1

Let the weight of triangle and square be x and y, then

x + y = 12 – 9 = 3 and 2y – x = (9 + 12) – 18 = 3

Then, adding the two equations,

3y = 6, y = 2

Therefore, x = 3 – y = 1.

So the answer is 1.

I prefer an algebraic approach, instead of actually working with the situation we get: Say $C$ is the weight of a circle, $T$ , the weight of a triangle and $Q$ , the weight of a square. We can write the equations to set the linear system, since all the scales are perfectly balanced:

$C+T+Q=9\\ C+2T+2Q=12\\ 2C+4T+Q=18$

which can be solved directly to give $C=6, T=1, Q=2$ .

1x + 1y + 1z = 9 1x + 2y + 2z = 12, thus the pro numerals are 6, x 1, y and 2, z

C+T+S = 9

C+T+S +T+S=12

therefore T+S=12-9 = 3

C+C +T+T+T+T+S = 18

therefore C+T+T+T = 9

because C+T+S=9 and T+S=3 then C=6 (6+3=9)

3T + C [6] = 9

So T = 1

From the first two balances, adding a triangle (T) and square (S) increases weight by three. So T + S = 3. And Circle (C) = 6 (from balance #1). Looking at the last balance, 4T+S+2C= 18. Since C=6, 4T+S=6. Since T+S = 3, we can subtract T+S from the 4T+S side and get 3T. And we can subtract 3 from 6 on the other side and keep the equality. 3T = 3. So T = 1. The weight of one Triangle is one.